What is Damping: Definition and 307 Discussions

Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. In physical systems, damping is produced by processes that dissipate the energy stored in the oscillation. Examples include viscous drag (a liquid's viscosity can hinder an oscillatory system, causing it to slow down) in mechanical systems, resistance in electronic oscillators, and absorption and scattering of light in optical oscillators. Damping not based on energy loss can be important in other oscillating systems such as those that occur in biological systems and bikes (ex. Suspension (mechanics)). Not to be confused with friction, which is a dissipative force acting on a system. Friction can cause or be a factor of damping.
The damping ratio is a dimensionless measure describing how oscillations in a system decay after a disturbance. Many systems exhibit oscillatory behavior when they are disturbed from their position of static equilibrium. A mass suspended from a spring, for example, might, if pulled and released, bounce up and down. On each bounce, the system tends to return to its equilibrium position, but overshoots it. Sometimes losses (e.g. frictional) damp the system and can cause the oscillations to gradually decay in amplitude towards zero or attenuate. The damping ratio is a measure describing how rapidly the oscillations decay from one bounce to the next.
The damping ratio is a system parameter, denoted by ζ (zeta), that can vary from undamped (ζ = 0), underdamped (ζ < 1) through critically damped (ζ = 1) to overdamped (ζ > 1).
The behaviour of oscillating systems is often of interest in a diverse range of disciplines that include control engineering, chemical engineering, mechanical engineering, structural engineering, and electrical engineering. The physical quantity that is oscillating varies greatly, and could be the swaying of a tall building in the wind, or the speed of an electric motor, but a normalised, or non-dimensionalised approach can be convenient in describing common aspects of behavior.

View More On Wikipedia.org
Recent contents Top users
  1. S

    How Do You Determine the Damping Constant from an Amplitude vs Time Graph?

    how can we find damping constant from graph of amplitude versus time?
  2. F

    What Is the Minimum Damping Constant to Limit Vibration Amplitude to 3.2 mm?

    Homework Statement A sensitive instrument with the mass of 30 kg should be installed in a labratory. In the labratory, there exist a machine that causes the floor to vibrate with the frequency of 0.8 Hz and with the amplitude 8.0 mm, each with the spring constant k = 500 N/m. Its then...
  3. K

    Critical damping vs overdamping

    why critical damping and over damping doesn't undergo oscillations?
  4. 1

    How can a part's geometry be used for damping or to reduce vibration?

    Hi, So basically I am wondering how can you increase damping within a part, just by altering its geometry. I've researched this topic, but haven't yet found anything significant. Here are my main findings: - Rayleigh Damping uses the equation: [C] = α[M] + β[K], which to me shows that mass...
  5. S

    Damping Properties of Rubber: Understanding the Impact of Strain Amplitude

    Hey Guys, Can anyone tell me why the damping properties of rubber will decrease as the strain amplitude increases? Thanks
  6. PsychonautQQ

    Damping factor in critical damping

    The position equation for a oscillator undergoing critical damping is given by x(t) = Ate^(-γt) + Be^(-γt) where γ = c/2m and c is from the original force equation ma + cv + kx = 0 γ is called the damping factor my book then goes on to say without explanation that γ = c/2m =...
  7. R

    What Constant c Achieves Critical Damping?

    Homework Statement Suppose a mass- spring is modeled by x''+ cx'+100x. What should the damping constant c be in order that critical damping occurs? Homework Equations The Attempt at a Solution I set the discriminant equal to zero so that there are real repeated roots. B^2-4ac=0...
  8. S

    Calculating Damping Ratio of SMAs Using Hysteresis Loops

    G'day guys, I am currently trying to calculate the damping ratio for Shape memory alloys using hysteresis loops. The damping ratio is usually represented as ΔU/2∏U, where ΔU is the energy lost due to material damping and U is the elastic strain energy. My problem is trying to find this...
  9. E

    How Do You Calculate the Damping Constant in a Sloped Car Scenario?

    This is actually for a engineering course in modelling, and not in physics per se, but it seems to me to be fairly basic physics. Apologies in advance if it's out of place. Homework Statement A car with a mass of 1000 kg is held still on a slope with an inclination of 5.8 °, and then let...
  10. A

    Forced SHM with damping problem

    Homework Statement A mass, m, attached to a spring hangs vertically downwards under gravity. It is subject to a viscous damping force proportional to its velocity. The spring constant is k > 0. A periodic force is applied to the spring and the equation of motion for the mass is \ddot x+...
  11. gfd43tg

    Damping Coefficient and Resonant Frequency of a 2nd order circuit

    Hello, I am having major confusion for how to find the damping coefficient, α, and the resonance frequency, ωo, for a second order circuit, in general. I know that there are tables for standard circuits like a series RLC and parallel RLC giving those values, but I am certain that I need to know...
  12. A

    DE: Critical Damping Oscillating?

    I'm having a problem understanding a critical damping model. I know critical damping is supposed to return the system to equilibrium as quickly as possible without oscillating, and a critically damped system will have repeated roots so the general solution will be: c1e^rt + c2te^rt But what...
  13. J

    Calculate damping coefficient of dashpot from physical dimensions

    Hi all, I am trying to calculate the damping coefficient of a linear viscous dashpot/damper given the dimensions of the piston, and the dynamic viscosity of the damping fluid. I have found this calculator, but does anyone know the equation that it uses...
  14. W

    Electromagnetic damping logarithmic decrement task

    Homework Statement The contour consists of a condenser with capacitance C = 2.22*10^-9 F and a coil of copper wire. The diameter of the wire 5*10^-4 m, the length of the coil 20*10^-2 m. Determine the damping logarithmic decrement Λ of the fluctuations? Given answer:0.018 Homework Equations...
  15. Z

    Solving Critical Damping Circuit: Find R, i, di/dt, v_C(t)

    Homework Statement In the circuit in the following figure, the resistor is adjusted for critical damping. The initial capacitor voltage is 15 V, and the initial inductor current is 6 mA. Find the numerical value of R. Find the numerical values of i immediately after the switch is closed...
  16. F

    Calculating Damping Coefficient of a Generator

    Hey, I understand that damper windings are used to stabilize the speed of the rotor under varying loads. The rotor speed is decreased or increased by the induction principle. Physically the damped windings are some sort of copper bars inserted into the pole faces of a rotor and all...
  17. W

    Damping Force in a piston: Ideal Gas versus a Fluid

    I was in my physics of the human body class and we got on the topic of pistons. It was given to me that the dampening force pertaining to such a piston filled with a gas is proportional to the square of the velocity of the piston; however, for fluids it was given as simply proportional to the...
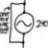
  18. jegues

    Nyquist plot, damping factor and phase margin

    Homework Statement A Nyquist (polar) plot of a standard second-order system is shown below (drawn to scale). Suppose a unit-step function is applied as the input to this system. Determine the peak percentage overshoot expected in the system output. Homework Equations The Attempt at a...
  19. D

    Calculation of range for signal with damping

    Homework Statement Given the transmitting power of 0.1 mW and received noise of -100 dBm. Consider a signal which needs a SNR of 30 dB. Calculate the range for a signal of 0.5 MHz given that the damping for the signal is calculated as: L = 10 +8.0*f [dB/km] where f is the...
  20. B

    What is the role of roll damping coefficient in aircraft performance?

    Hello, I am new to Aerodynamics and am having trouble understanding what exactly the roll damping derivative is. The roll damping derivative is a measure of the change in rolling moment coefficient with respect to nondimensional roll rate and is usually negative. Does that mean a glider...
  21. B

    Damping ratio from Eddy current breaking

    Hello All, I have been asked to design and build a rig that will introduce the concept of a mass spring damper system to mechanical engineers in their early years of university. To make it slightly more complex, the rig needs to be torsional rather than linear. My design so far is to use a...
  22. G

    Damping conditions for multi degrees of freedom

    I know that d^2<4mk for underdamped, d^2>4mk for overdamped and d^2=4mk for critically damped. This is true if there is only 1 mass and spring and damper. How to use these equations if I have 2 mass, 3 spring and 3 dampers. That is d,m,k are in 2x2 matrices. Please some one help me with this.
  23. H

    Find damping coefficient at a given vibration mode

    I am working on a motorcycle dynamics problem. I have written the equations of motion in matrix form in MATLAB (and mathcad). It is a 4 degree of freedom system, so I have a mass, damping and stiffness matrix all 4X4. I am able to find from these matrices the natural frequencies, and damping...
  24. L

    Simple Harmonic Oscillator and Damping

    Homework Statement After four cycles the amplitude of a damped harmonic oscillator has dropped to 1/e of it's initial value. Find the ratio of the frequency of this oscillator to that of it's natural frequency (undamped value) Homework Equations x'' +(√k/m) = 0 x'' = d/dt(dx/dt)...
  25. R

    Determining the damping constant from the ratio of amplitudes

    Homework Statement I have measured the amplitude between the first and tenth oscillations for a damped harmonic oscillator (spring with a mass attached). I also have measured the period. First question. Is an (underdamped) harmonic oscillator periodic? Like I know that the solution to the...
  26. C

    Eddy current damping - Analysis?

    I'm trying to damp an oscillating metal plate with a neodymium magnet. Things I know - Remanence of the magnet - The magnetic flux density at distance z (from the distributors site) - Dimensions of the magnet - Plate material (Aluminium) - Distance to the plate. What I'm trying to find out is...
  27. R

    Springs with the least amount of damping?

    I have a project I'm tinkering with that involves a "gyroscope" that I want to rotate back and forth using a spring. The gyroscope is a piece of steel pipe with a 4in ID about a foot long that weighs roughly 10lbs or so. I have a 5/16ths rod going down the center as an axle and it's running on...
  28. F

    External damping force in Mass Spring Damper system

    Hi, I am designing a wave energy converter, which has one degree of freedom - heaving motion. Meaning it will move only in vertical direction. My system can be considered as a Mass Spring Damper system. Thus my equation of motion is: F=Fh+Fe Where, Fe= Excitation force...
  29. C

    Estimating the damping ratio from the waveform graph

    Homework Statement From the waveform shown below, estimate a) the damping ratio ζ (you may compare response with a standard chart); b) the forced or damped frequency of oscillation; and c) the natural or undamped frequency of oscillation. Homework Equations Since the waveform is under...
  30. H

    Equivalent stiffness and damping

    Homework Statement A scheme of springs and dampers is given. What is equivalent stiffness and damping? Homework Equations For stiffness in series: keq=ka*kb/(ka+kb) For stiffness in parallel: keq=ka+kb For dampers similarly. The Attempt at a Solution To me it looks like k1 and k2 are in...
  31. C

    Knowing Damping and Spring Constant Finding Time

    Homework Statement A spring with a force constant of 1.50 N/m is attached to a mass of 120 g. The system has a damping constant of 0.0180 Ns/m. How long does it take the amplitude of the oscillations to decrease from 10.0 mm to 5.00 mm? Homework Equations (double dot)x +(c/m)(one...
  32. S

    Effect of electromagnetic damping with variable current

    Hi guys, first time poster. My question is; How would a constant damping provided by an electromagnet affect the damping ratio (and logarithmic decrement) amplitude? And how would increasing the current through the electromagnet affect the damping? So far I've found Biot-Savart's Law which...
  33. D

    Forced oscillations without damping

    Homework Statement We are to develop the equations of motion for an undamped horizontal spring system, the mass of which is being driven by a periodic force: F=F0 cos wt. I know how to do it but my teacher has defined an odd term, the meaning of which I want to be clarified. Homework...
  34. D

    Practical uses of oscillator damping

    Homework Statement Hi guys, The title says it all pretty much. I need to know a handful of practical uses for each of the following, in the context of oscillatory motion (springs, pendulums etc): 1) light damping 2) critical damping 3) heavy damping Homework Equations Light...
  35. M

    Rayleigh Damping: Exploring the Dynamics of a 1D System

    Hi there, I came across the concept of Rayleigh damping. I aqm told it is unrelated to viscoelasticity and as a result is unable to reproduce the behaviour of real materials under harmonic excitation. I can not understand why. Considering for simplicity a 1D setting, a ball of mass...
  36. E

    Estimating damping factor for steel in flexural oscillation

    I am trying to estimate the damping ratio of steel in bending. I have a situation where I need to know the dynamic response of an inverted pendulum. A picture is worth a thousand words, so here you go: The vibration will be free; it is caused be the initial position of the system. I can...
  37. U

    Suspension strut design (diff eq and damping systems)

    Homework Statement The mass of a car that acts on one wheel is 100 kg. The elasticity (spring) constant in the suspension system of that wheel is k= 10^4 N/m: Design the strut (find the friction/resistance constant c) such that any vertical motion of the wheel (set up for example by going...
  38. A

    Spring Differential Equation w/ Damping

    Homework Statement A spring with a spring constant of 20 pounds per foot is loaded with a 10-pound weight and allowed to reach equilibrium. It is then displaced 1 foot downward and released. If the weight experiences a retarding force in pounds equal to four times the velocity at every point...
  39. V

    How Do You Calculate K for a Closed Loop Damping Ratio in Higher Order Systems?

    From control systems: I am asked to find the value of K that gives the closed loop damping ratio of 1/sqrt2. The value for the complimentary sensitivity is T(S)=(2KS +4K)/(s^3 +162S^2 +(320+2K)S +4K) so how do I find the value for K? I tried putting it in the general equation, but it...
  40. G

    Theory of Damping: General Equation?

    Is there a general equation of damping? I know that there is a second ODE for damping with regards to springs, and with RLC circuits, but is there a general form of damping equations (with critical-damp, overdamp, and under-damp). I know how to solve second ODEs, but I was wondering if there was...
  41. J

    Am I correct in saying the mass of a pendulum bob affects its damping rate

    How does the mass of a pendulum bob affect the time taken for the oscillation of a pendulum to diminish? At first I instinctively thought that it would have no effect. However, thinking about the pendulum bob's momentum as it interacts with the air molecules, a higher massed pendulum should...
  42. J

    Graph help on Damping effects on SHM experiment

    1. The problem Okay. So just too briefly outline my experiment: I have a pendulum bob attached to two cardboard discs, and am testing to see how the radius of the cardboard discs effects the damping of the simple harmonic oscillator (the pendulum). I have results (such as the one below which...
  43. N

    Problems with Critical Damping and Underdamping

    Homework Statement The concept of damping is new to me and the problems I have seen have had different known values than I see in the equations I have. Here's two I am working on. 1) An automobile suspension is critically damped, and its period of free oscillation with no damping is 1s...
  44. R

    How to find damping ratio, revision questions.

    Hi guys, Revision for an exam tomorrow, I hope someone can help? I've been given the answers but I can't work out how to find the damping ratio without being given a velocity or distance for the mass to travel?A mass of 6kg is suspended on a spring and set oscillating. it is observed that...
  45. Z

    Estimate Damping Coefficient of Car with Hand Bouncing & Dropping

    I was wondering how I can estimate the damping coefficient of my car by doing the hand bouncing the car body and watching the motion of the car? Mechanics usually bounce the car by applying hand force and watching how the car moves in harmonic motion. Is there a way to estimate the damping...
  46. Z

    Estimating spring coeff and damping coeffient of my car

    I'm working on a project, I just need ballpark estimates for the spring constant and damping coefficient for my 1994 Nissan Pathfinder SUV. I was thinking of using Hookes law to estimate the spring constant, can I just measure the ride height of the car with nothing in it, then add 200 pounds...
  47. bhobba

    Speaker Back And Forth Motion Damping

    Hi Guys I usually post in the Quantum Physics section because that in my interest these days. I have recently been in a rather heated discussion about an interesting device a speaker designer I know (Mike Lenehan) recently bought to market...
  48. S

    How Does Damping Affect the Dynamics of a Spring-Mass System?

    Homework Statement Spring – mass system with spring constant k = 40 N/m and mass 10 kg. a. Find the angular speed and period. Draw the response X versus time t b. Linear damping is added with ζ = 4 %. Find the angular speed and period. Draw the response c. Viscous damping is added with c1 =...
  49. T

    Work energy problem with damping?

    Homework Statement I need help with part d. The Attempt at a Solution I worked out the damping constant and I am pretty sure it is correct. So I tried to solve this using work energy theorem. I ended up with a quadratic equation and solved for two solutions. None of them match the answer...
  50. T

    Determine critical damping of multimass system

    Hi I have a spring mass damper system with multiple masses. Is there any way I can calculate the magnitude of the damping in order to get a critical damped system? I have the scaling of the dampers(c1/c2) and they are connected in series. c_eq=c1+c2... I tried with the formula...
Back
Top