Definition Definition and 1000 Threads
-
R
I How can we define a limit approaching negative infinity?
I have the following definition: $$ \lim_{x\to p^+}f(x)=+\infty\iff \forall\,\,\varepsilon>0,\,\exists\,\,\delta>0,\,\,\text{with}\,\,p+\delta< b: p< x < p+\delta \implies f(x) > \varepsilon$$ From this, how can I get the definition of $$\lim_{x\to p^-}=-\infty? $$ -
R
MHB What is the definition of a negative infinity limit?
I have the following definition: $$\lim_{x\to p^+}f(x)=+\infty\iff \forall\,\,\varepsilon>0,\,\exists\,\,\delta>0,\,\,\text{with}\,\,p+\delta< b: p< x < p+\delta \implies f(x) > \varepsilon$$ From this, how can I get the definition of $$\lim_{x\to p^-}=-\infty? $$ -
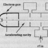
Acceleration in Polar Coords, Intuitive Definition video
Summary:: I wish this video (and YouTube in general) was around when I took intermediate level mechanics as an undergraduate physics student: I wish this video (and YouTube in general) was around when I took intermediate level mechanics as an undergraduate physics student:- CPW
- Thread
- Acceleration Definition Polar Video
- Replies: 2
- Forum: STEM Academic Advising
-
T
A Hypersurface Definition Confusion in General Relativity
In my notes on general relativity, hypersurfaces are defined as in the image. What confuses me is that if f=constant, surely the partial differential is going to be zero? I'm not sure if I'm missing something, but surely the function can't be equal to a constant and its partial differential be...- tm33333
- Thread
- Definition Differential geometry
- Replies: 5
- Forum: Special and General Relativity
-
T
Definition of a system in Boltzmann entropy
Context Boltzmann first defined his entropy as S = k log(W). This seems to be pretty consistently taught. However, the exact definitions of S & W seem to vary slightly. Some say S is the entropy of a macrostate, while others describe it as the entropy for the system. Where the definition of...- timjdoom
- Thread
- Boltzmann Definition Entropy System
- Replies: 1
- Forum: Thermodynamics
-
K
I Questions about the definition of a metre (A. P. French's book)
In his book, Newtonian Mechanics, while describing the standard unit for length, A. P. French writes (being American, he uses meter and not metre): My questions are twofold: The first one is about the physics. What does the text in orange really mean? There is no sidebar about "optical...- KedarMhaswade
- Thread
- Book Definition
- Replies: 17
- Forum: Classical Physics
-
U
Clarification on electric quadrupole moment definition
I have encountered two (?) definitions of the electric quadrupole moment. They are: $$Q_{ij}=\frac{1}{2}\int \rho(\vec{x}')x'_i x'_j\,\mathrm{d}^3x'$$ and $$Q_{ij}=\int (3x'_i x'_j-\delta_{ij}x'^2)\rho(\vec{x}')\,\mathrm{d}^3x'$$ I am trying to study radiation arising from the electric...- user1139
- Thread
- Definition Electric Electromagnetism Moment Radiation Tensors
- Replies: 5
- Forum: Advanced Physics Homework Help
-
H
Determining the growth of two functions using Big-Oh definition
My attempt involved using the big-Oh notation, I think this should work but I am not sure how to go about it. The two functions are g(n) = 6^n/n^5 and h(n) = (ln n)^84. I thought that I could use the inequality 6^n < ln(n)^84 and 6^n/|n^5| = |g(n)| < 6^n and put those inequalities together...- Haku
- Thread
- Definition Functions Growth
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-

B Sequential Compactness of Sets: A Definition
Definition: A set is sequentially compact if all sequences contained in the set contain a subsequence that converges to a point in the set. Let ##N\in \mathbb{N}## and suppose that ##m\geq N##. Let ##x\in K_m##. Since ##K_m\subset K_{m-1}\subset \ldots \subset K_N##, it follows that ##x## is an...- Eclair_de_XII
- Thread
- Definition Sets
- Replies: 10
- Forum: Calculus
-

I Definition of Tensor Identity Simplification
Is there a simplifcation of ##g^{\alpha \delta}g_{\beta \gamma} ## or what is equal to ?- Arman777
- Thread
- Definition Identity Tensor
- Replies: 3
- Forum: Special and General Relativity
-
A
Can a supernatural phenomenon by definition exist?
Or would any apparent supernatural phenomenon ultimately be boiled down to natural laws that we just don't understand yet? By definition, a supernatural phenomenon doesn't obey natural laws, or a certain subset of natural laws. Like say for instance, we observer a large star orbiting a small...- AndromedaRXJ
- Thread
- Definition Phenomenon
- Replies: 25
- Forum: General Discussion
-
S
I Subset definition: universal quantifier over which set?
This is a somewhat trivial question, but I never managed to learn much logic back in the day...so: The definition of a subset can be written as: ## A \subset B \Leftrightarrow \forall x (x \in A \Rightarrow x \in B) ## However, over which set is ##\forall## supposed to quantify? It seems to...- strauser
- Thread
- Definition Set Universal
- Replies: 33
- Forum: Set Theory, Logic, Probability, Statistics
-
B
The definition of generalised momentum
Why, in lagrangian mechanics, do we calculate: ##\frac{d}{dt}\frac{\partial T}{\partial \dot{q}}## to get the (generalised) momentum change in time instead of ##\frac{d T}{dq}##? (T - kinetic energy; q - generalised coordinate; p - generalised momentum; for simplicity I assumed that no external... -
F
[Complex analysis] Contradiction in the definition of a branch
I find the following definition in my complex analysis book : Definition : ## F(z)## is said to be a branch of a multiple-valued function ##f(z)## in a domain ##D## if ##F(z)## is single-valued and continuous in ##D## and has the property that, for each ##z## in ##D##, the value ##F(z)## is one...- fatpotato
- Thread
- Analysis Branch Branch cut Complex analysis Contradiction Definition
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-
E
Definition of energy level width
First, it is easy to see that n=4 after the collision because: E_1=-13.6\frac{1^2}{1^2}eV=-13.6eV E_4=-13.6\frac{1^2}{4^2}eV=-0.85eV E_5=-13.6\frac{z^2}{5^2}eV=-0.544eVBut, I never saw a definition for the width of an energy level. I tried to use something I saw online that said it was...- Eitan Levy
- Thread
- Definition Energy Energy level Width
- Replies: 3
- Forum: Introductory Physics Homework Help
-
A
Domain of definition of the function f(x,y)=x^y
Good day as said in the title i need the domain of definition of of the function f(x,y)=x^y for me as x^y=expontial (y*ln(x)) so x>0 but the solution said more than that I really don't understand why we consider the case (0,y) in which while should be different from 0, because I will never...- Amaelle
- Thread
- Definition Domain Function
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
L
MHB Is Every Statement Correct in Defining an Onto Function?
Which of the following statements is equivalent to saying that a function f:A→B is onto? There are 8 options, select all that are correct. x f(A)=B x In the arrow diagram representing f, every point in B has an arrow pointing at it. x ∀y∈B ∃x∈A such that f(x)=y x f−1(B)=A...- lemonthree
- Thread
- Definition Function
- Replies: 6
- Forum: General Math
-

B What is the Definition of a Candela?
I'm trying to wrap my head around the definition of a candela: "The candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540×10^12 hertz and that has a radiant intensity in that direction of 1/683 watt per steradian." I'm aware...- SamRoss
- Thread
- Definition
- Replies: 10
- Forum: Classical Physics
-
E
B What is Energy? A Clear Definition and Explanation
Hello there, I have heard countless times about the word energy, but I still don't know what exactly an energy is. Like for example, we know the definition of a physical quantity called velocity which by definition is change in displacement (so we can easily describe what a velocity is). We...- EnricoHendro
- Thread
- classic physics definition energy intro physics physcis
- Replies: 43
- Forum: Classical Physics
-

Definition of potential energy
Potential energy is generally a function of position vector ##\vec r## and it is defined as ##\int_i^f \vec F(\vec r)d\vec r=-U(\vec r) \bigg| _{i}^{f}=U(\vec r_i)-U(\vec r_f)##, where the force is conservative. Using the fact that the integral of force is also the definition of work, I obtain... -
F
Velocity definition and parameter dependence
Hello Forum, Limiting our discussion to 1D motion, it is clear that the concept of instantaneous velocity is defined as the covered displacement dx divided by the time interval elapsed dt: $$ v = \frac {dx}{dt}$$ However, mathematically, the velocity ##v## can be made to depend on any... -
S
B What is Plasma? Is Tungsten Vapour a Gas or Plasma?
What is "plasma"? How is a fluid measured to be either a gas or a plasma? Mercury boils at 359 Celsius (632 Kelvin). Mercury vapour is poorly conductive, little ionized (incidentally - monoatomic) and generally defined as a gas. However, tungsten boils at 5930 C (6203 K). Photosphere of Sun...- snorkack
- Thread
- Definition Plasma
- Replies: 3
- Forum: Atomic and Condensed Matter
-
M
I Is There a Set Definition for Propositions in Propositional Logic?
In propositional logic we study rules of logical inference from propositions, such as ## (p\rightarrow q) \leftrightarrow (\lnot q \rightarrow \lnot p) ##, or ## \lnot (p \land \lnot p) \leftrightarrow (p \lor \lnot p) ##. Do we ever define the set of propositions we are dealing with? Some...- madness
- Thread
- Definition
- Replies: 27
- Forum: Set Theory, Logic, Probability, Statistics
-

Equation Alternatives for Young's Modulus
I just found a definition to the Young modulus as: Is this a plausible representation of Y? That is, i know the definition , i don't think we can say this definition and the first definition is equal.- LCSphysicist
- Thread
- Definition Modulus Young's modulus
- Replies: 14
- Forum: Introductory Physics Homework Help
-

What is the definition of cathode in the photoelectric effect?
We know anode=oxidation=loss of electrons and cathode=reduction=gain of electrons but in the photoelectric effect the electrons are gained at the anode and lost at the cathode of the discharge tube? References: Anode, Cathode, Oxidation, Reduction- Rongeet Banerjee
- Thread
- Cathode Definition Photoelectric effect
- Replies: 1
- Forum: Introductory Physics Homework Help
-
J
B What is the definition of a black hole?
Hi All, This is my first post, so please bare with me and if I am going all wrong about, please let me know. The definition of a black hole according NASA; 'A black hole is a place in space where gravity pulls so much that even light can not get out'. Now I am not challenging this at all...- JoeyJoystick
- Thread
- Black hole Definition Hole
- Replies: 27
- Forum: Astronomy and Astrophysics
-
S
The mathematical definition of "wave"?
Is there a standard mathematical definition for "wave"? What is the definition? Assuming that there is a definition, what are the mathematical definitions of the properties of waves? For example, how is the "group" of a wave defined? ( as in the "group" that has a "group velocity"). I'm not...- Stephen Tashi
- Thread
- Definition Mathematical Wave
- Replies: 61
- Forum: General Math
-
S
I Does the definition of cardinality assume distinguishability?
Physics speaks of a set S of N "indistinguishable particles", giving the set S a cardinality but forbidding any equivalence relation that can distinguish between two particles. Is this terminology inconsistent with the mathematical definition of cardinality? Suppose ##S## is a set with...- Stephen Tashi
- Thread
- Cardinality Definition
- Replies: 9
- Forum: Set Theory, Logic, Probability, Statistics
-
J
Difference between abstraction layers and modularisation
I understand abstraction to be the process of representing a system, concept or process in simple terms, leaving out finer details which may obfuscate the bigger picture. My understanding of layers of abstraction is that it refers to different depths of understanding of a concept where each...- JC2000
- Thread
- Definition Difference Networks
- Replies: 10
- Forum: Programming and Computer Science
-
S
Definition of temperature in weather reporting
In my town, newspaper stories say we've had several days of record high temperatures. The stories report temperatures in the range of 107 F. However, on the same days, online weather reports show temperatures as high as 116 F. I think online weather reports use reports from amateur weather...- Stephen Tashi
- Thread
- Definition Temperature Weather
- Replies: 5
- Forum: Earth Sciences
-
S
B Why is There No Factor of 1/2 in the Torsion Tensor Definition?
Let's say we have any two covariant derivative operators ##\nabla## and ##\nabla'##. Then there exists a tensor ##C^{\alpha}_{\mu\nu}## such that for all covariant vectors ##\omega_{\nu}##,$$\nabla_{\mu}\omega_{\nu}=\nabla'_{\mu}\omega_{\nu}-C^{\alpha}_{\mu\nu}\omega_{\alpha}$$ Now I'm quoting...- Shirish
- Thread
- Definition Doubt Tensor Torsion
- Replies: 3
- Forum: Differential Geometry
-

I Understanding the ##\epsilon## definition of this integral
Integrals are defined with the help of upper and lower sums, and more number of points in a partition of a given interval (on which we are integrating) ensure a lower upper sum and a higher lower sum. Keeping in mind these two things, I find the following definition easy to digest A function... -
P
Polarization of Scattered Radiation, motivating definition?
Figure from Jackson, the ##0## subscripts indicate incident waves whereas the lack of subscripts indicate the scattered wave. Figure from Zangwill, the hat ##\hat{e}## vectors are for the incident electric field. We are dealing with unpolarized light so we have two orthogonal polarization...- PhDeezNutz
- Thread
- Definition Polarization Radiation
- Replies: 3
- Forum: Introductory Physics Homework Help
-
E
A peculiar definition of work on Wikipedia
I came across this here: Is this incorrect? If we setup any coordinate system and take torques about that coordinate system, then I would have thought we say the work done in that frame is $$W = \int_{C} \vec{F} \cdot d\vec{r} = \int_{C} \vec{\tau} \cdot d\vec{\theta} \quad \left( = \int_{C}...- etotheipi
- Thread
- Definition Wikipedia Work
- Replies: 3
- Forum: Mechanics
-
N
Conceptual Definition of Intelligence
Summary:: We are fundamentally wrong in our understanding of what intelligence is. Intelligence is believed to be some manner of product of the size and scope of computing. Fundamentally stupid way of thinking. Intelligence is a function of the relationship between the size of a computation...- Namewastaken
- Thread
- Conceptual Definition Intelligence
- Replies: 11
- Forum: General Discussion
-
G
MHB Derivative using the limit definition (without using L'Hospital's rule)
Hello everybody, could you help me with this problem please? I have to find a derivative in x0 of this function (without using L'Hospital's rule): I used the definition , but I don't know what to do next. Thank you.- goody1
- Thread
- Definition Derivative Limit Limit definition
- Replies: 4
- Forum: General Math
-

I Four-Velocity: Geometric Definition
In a formal manner the 4-velocity defined as ##\vec{u} = \frac{d\vec{x}}{cd\tau}##. Now this is also equal to the unit tangent vector of the worldline. My confusion is actually more geometrical. ##d\vec{x}## is the infitesimal distance between two points in the worldline and ##cd\tau## is the...- Arman777
- Thread
- Definition
- Replies: 17
- Forum: Special and General Relativity
-

Optical Looking for a high definition DIY spectrometer
Hello people, I am looking for a high definition DIY spectrometer website or resource. If you find a good one please let me know. I've watched several youtube videos about it, used both googles and duckduckgo but I am left unsatisfied. There are several things I do not understand, both about...- fluidistic
- Thread
- Definition Diy Spectrometer
- Replies: 7
- Forum: DIY Projects
-

What is the standard definition for what an "electric source" is?
The syllabus states : "Explain that the potential difference which is needed to apply across any electric circuit to flow current is supplied by an electric source". To explain this and make notes, I want to first understand what an electric source particularly is. And how all those electric...- nineteen
- Thread
- Current Definition Elecricity Source Standard
- Replies: 4
- Forum: Electromagnetism
-

Definition of Rheology : Irreversible or not?
In Agricultural Process Engineering(Third Edition) by S.M. Henderson and R.L. Perry, Rheology is described as "... the science that considers stress-strain relations where flow proceeds irreversibly with time. Creep in metals and concrete and the strength properties of fruits and vegetables are...- hizballah_arham
- Thread
- Definition Irreversible
- Replies: 1
- Forum: Materials and Chemical Engineering
-
G
MHB How Do You Prove Limits at Infinity?
Hi, can anybody help me with this two limits? I have to prove them by the definition of limit. Thank you in advance.- goody1
- Thread
- Definition Limit
- Replies: 3
- Forum: General Math
-
C
I Definition of a Degenerate Subspace (QM)
I was learning about Degenerate Perturbation Theory and I encountered the term 'Degenerate Subspace', I didn't really understand what it meant so I came here to ask - what does it mean? will it matter if i'll say 'Degenerate space' instead of 'Degenerate Subspace'? and subspace of what? (...- CGandC
- Thread
- Definition Degenerate perturbation theory Perturbation theory Qm Quantum mechanics Subspace
- Replies: 12
- Forum: Quantum Physics
-
M
B What Does it Mean When We Say the Universe is 'Flat'?
When we say the universe is "flat," do we mean: 1) If you could hypothetically "zoom" out to the edge of the universe it would appear roughly as a flat like a sheet of paper with local fluctuations / bumps to indicate the presence of matter. 2) If we draw 2 parallel lines from 1 location they...- MikeeMiracle
- Thread
- Definition Flat Flat universe Universe
- Replies: 3
- Forum: Cosmology
-
M
Engineering Power Loss Definition in a Damped Wave Equation (Skin Depth Problem}
Hi, So the main question is: How to deal with power loss in E-M waves numerically when we are given power loss in dB's? The context is that we are dealing with the damped wave equation: \nabla ^ 2 \vec E = \mu \sigma \frac{\partial \vec E}{\partial t} + \mu \epsilon \frac{\partial ^ 2 \vec...- Master1022
- Thread
- Damped Definition Depth Loss Power Power loss Wave Wave equation
- Replies: 1
- Forum: Engineering and Comp Sci Homework Help
-

Is this a good alternative definition of electron affinity?
traditional definition of electron affinity: the amount of energy released by an element in its gas form when gaining an electron second definition?: the stability gained by an element in its gas form when gaining an electron (e.g. halogens are more stable after gaining an electron, and when...- sneakycooky
- Thread
- Definition Electron Electron affinity Energy Stability
- Replies: 3
- Forum: Chemistry
-
M
MHB Check existence of limit with definition
Hey! :o I want to check the existence of the limit $\lim_{x\to 0}\frac{x}{x} $ using the definition. For that do we use the epsilon delta definition? If yes, I have done the following: Let $\epsilon>0$. We want to show that there is a $\delta>0$ s.t. if $0<|x-0|<\delta$ then... -
S
The definition of the proper time
I wonder what is the proper time, the time passed on the train or the time of the observer? If there is another people on the train, we see the train as a frame, so is the time on the train the proper time or the time of rest frame?- shallod
- Thread
- Definition Proper time Time
- Replies: 3
- Forum: Introductory Physics Homework Help
-
M
A Definition of the IAU for the ecliptic plane
How is the definition of the IAU for the ecliptic plane? In particular I am interested how the perturbations are treated. Neither the Earth nor the common gravity center of Earth and moon move on an exact plane around the sun. I found the IAU document “Adoption of the P03 Precession Theory and...- member 672147
- Thread
- Definition Ecliptic Plane
- Replies: 2
- Forum: Astronomy and Astrophysics
-

MHB Continuity of a Function .... Conway, Definition 1.7.1 .... ....
I am reading John B. Conway's book: A First Course in Analysis and am focused on Chapter 1: The Real Numbers ... and in particular I am focused on Section 1.7: Continuous Functions ... I need help with clarifying Definition 1.7.1 ...Definition 1.7.1 reads as follows: My question is as...- Math Amateur
- Thread
- Continuity Definition Function
- Replies: 3
- Forum: Topology and Analysis
-
F
What is the Definition of Derivative and How is it Proved?
Proof: By definition of derivative, $$f'(a) = \lim_{x\rightarrow a}\frac{f(x) - f(a)}{x - a}$$ exists and is finite. Let ##(x_n)## be any sequence that converges to ##a##. By definition of limit, we have $$\lim_{x_n\rightarrow a} \frac{f(x_n) - f(a)}{x_n - a} = f'(a)$$. By definition of...- fishturtle1
- Thread
- Definition Derivative
- Replies: 7
- Forum: Calculus and Beyond Homework Help