Delta Definition and 1000 Threads
-

A Dirac Delta: Normal -> Lognormal?
Hello shipmates, Instead of imagining a Dirac Delta as the limit of a normal, like this: $$ \delta\left ( x \right ) = \lim_{a \to 0}\frac{1}{|a|\sqrt{2\pi}}\exp\left [ -\left ( x/a \right )^2 \right ] $$ Could we say the same thing except starting with a lognormal, like this? $$ \delta_{LN}...- Steve Zissou
- Thread
- Delta Dirac Normal
- Replies: 11
- Forum: General Math
-
M
Calculating phase currents from line currents in an unbalanced delta
In an unbalanced delta system, I can calculate the line currents given the phase currents. However, I seem to be unable to go the other direction and cannot find sufficient resources to do so. Looking at the phasor diagrams it seems like this should be possible, but my math (or understanding of...- mrcavemen
- Thread
- Delta
- Replies: 35
- Forum: Electrical Engineering
-

Solving for Speed & Revolution: F * delta t = p
Honestly i have very little idea. F * delta t = p F * delta t /m = v So i know the speed of the rod And i know that however high the rod is supposed to go, when its back down it should have done excactly one revolution. I have the feeling that I should So probably i have to use something like...- Justforthisquestion1
- Thread
- Delta Delta t Revolution Speed
- Replies: 13
- Forum: Introductory Physics Homework Help
-
S
I What kind of differential does the small Greek delta letter represent?
δ I had always thought that it represents a differential element for a parameter that it is not supposed to be a well-defined function - e.g., for a differential or heat or work in thermodynamics - as opposed to a regular Latin d, which is supposed to be such a well-defined function. However...- swampwiz
- Thread
- Delta Differential
- Replies: 2
- Forum: Differential Equations
-

I Fermi's golden rule: why delta function instead of density states?
Sakurai, in ##\S## 5.7.3 Constant Perturbation mentions that the transition rate can be written in both ways: $$w_{i \to [n]} = \frac{2 \pi}{\hbar} |V_{ni}|^2 \rho(E_n)$$ and $$w_{i \to n} = \frac{2 \pi}{\hbar} |V_{ni}|^2 \delta(E_n - E_i)$$ where it must be understood that this expression is...- yucheng
- Thread
- Delta Delta function Density Fermi's golden rule Function Quantum mechanics States
- Replies: 5
- Forum: Quantum Physics
-
H
Kramers-Kronig, parity and delta function
Hi, First of all, I'm not sure to understand what he Kramers-kronig do exactly. It is used to get the Real part of a function using the imaginary part? Then, when asked to add a peak to the parity at ##\omega = -\omega_0##, is ##Im[\epsilon_r(\omega)] = \delta(\omega^2 - \omega_0 ^2)## correct...- happyparticle
- Thread
- Delta Delta function Electro dynamics Function Parity
- Replies: 5
- Forum: Advanced Physics Homework Help
-

Help with the derivative of the Dirac delta
My goal is to develop the equation 21. You should asume that \delta(r_2-r_1)^2 =0. These is named renormalization. Then my question is , do my computes are correct with previous condition ?- Delerion24
- Thread
- Delta Derivative Dirac Dirac delta Dirac delta function
- Replies: 4
- Forum: Advanced Physics Homework Help
-
H
I ##\epsilon - \delta## proof and algebraic proof of limits
It occurred to me that I should ask this to people who passed the stage in which I’m right now, being unable to find anyone in my milieu (maybe because people around me have expertise in other fields than mathematics) I reckoned to come here. Let’s see this sequence: ## s_n =...- Hall
- Thread
- Delta Epsilon delta proof Limit Limits Proof
- Replies: 48
- Forum: Topology and Analysis
-

I Kronecker Delta: Order of Indices Explained
Hi everyone, I am a new member and would like to ask a naive simple (my guess) question. I am reading Weinberg’s Gravitation and Cosmology. On page 59, Eq. 2.12.10 therein reads $$ \begin{aligned} \left[\sigma_{\alpha \beta}\right]_{\gamma \delta}{}^{\varepsilon \zeta} &=\eta_{\alpha \gamma}...- Jim Lai
- Thread
- Delta Indices
- Replies: 5
- Forum: Special and General Relativity
-

Calculating fill rate if pressure delta, volume, and time are known?
I am looking for an equation that I can use to compute L/min or mL/min for a 480cc vessel going from 150bar to 250bar with a fill time of 6min. Sensors for flow rate at these pressures are hard to find, but I thought there might be a way to work this out with the parameters known. An equation...- wruehl1
- Thread
- Delta Pressure Rate Time Volume
- Replies: 10
- Forum: Mechanical Engineering
-
M
B Why is Delta y not equal to dy for infinitesimally dx on the graph?
Hello! As is known, \Delta y = dy for infinitesimally small dx. It's true. But if we have graph we may see that \Delta y isn't equal to dy even for infinitesimally small dx. Why is that so? Thanks! -
H
Sifting property of a Dirac delta inverse Mellin transformation
Hi, I have to verify the sifting property of ##\frac{1}{2\pi i} \int_{-i\infty}^{i\infty} e^{-sa}e^{st} ds## which is the inverse Mellin transformation of the Dirac delta function ##f(t) = \delta(t-a) ##. let ##s = iw## and ##ds = idw## ##\frac{1}{2\pi} \int_{-\infty}^{\infty} e^{-iwa}e^{iwt}...- happyparticle
- Thread
- Delta Dirac Dirac delta Inverse Property Transformation
- Replies: 31
- Forum: Calculus and Beyond Homework Help
-
H
Mellin transform of Dirac delta function ##\delta(t-a)##
Hi, I found Laplace transform of this Dirac delta function which is ##F(s) = e^{-st}## since ##\int_{\infty}^{-\infty} f(t) \delta (t-a) dt = f(a)## and that ##\delta(x) = 0## if ##x \neq 0## Then the Mellin transform ##f(t) = \frac{1}{2 \pi i} \int_{\gamma - i \omega}^{\gamma +i \omega}...- happyparticle
- Thread
- Delta Delta function Dirac Dirac delta Dirac delta function Function Laplace transform Transform
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-

New SARS-Cov-2 variant, "Deltacron" = Delta + Omicron variants
https://www.msn.com/en-us/health/medical/there-may-be-a-new-covid-variant-deltacron-heres-what-we-know-about-it/ar-AAUSuZi So there appear to be subvariants, or different combinations of Delta+Omicron.- Astronuc
- Thread
- Delta
- Replies: 1
- Forum: Biology and Medical
-

A Prove a formula with Dirac Delta
Why is the Laplacian of ##1/r## in spherical coordinates proportional to Dirac's Delta, namely: ##\left(\frac{\partial^2 }{\partial r^2}+\frac{2}{r}\frac{\partial }{\partial r}\right)\left(\frac{1}{r}\right)=-\frac{\delta(r)}{r^2}## I get that the result is zero. -
P
Scattered State Solutions of a Repulsive Dirac Delta Potential
I feel that this problem can be directly answered from the E>0 case of the attractive Dirac delta potential -a##\delta##(x), with the same reflection and transmission coefficients. Can someone confirm this hunch of mine?- PhysicsTruth
- Thread
- Delta Dirac Dirac delta Potential Potential well State
- Replies: 1
- Forum: Advanced Physics Homework Help
-
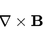
Delta function to calculate density of probablity
- anaisabel
- Thread
- Advance physics Delta Delta function Density Density function Function
- Replies: 9
- Forum: Advanced Physics Homework Help
-
R
Driven oscillator amplitude steady state X(t) = ##Asin(\omega t + \delta)##
I found ## \frac{\gamma}{2} = 7##, ##\gamma = 14## ##\omega_0^2 = \omega_d^2 + \frac{\gamma^2}{4} = 25## ##\omega_0 = \omega = 25##, thus ##\delta = \frac{\pi}{2}## ##A = \frac{\frac{F_0}{m}}{\sqrt((\omega_0^2 - \omega^2)+ \gamma^2\omega^2)} = 0.04## Thus, ##X(t) = 0.04sin(25t + \frac{\pi}{3} -...- Redwaves
- Thread
- Amplitude Damped oscillation Delta Driven oscillator Oscillator State Steady Steady state
- Replies: 18
- Forum: Introductory Physics Homework Help
-

With Delta Attending School A Difficult Dilemma
See: https://www.medrxiv.org/content/10.1101/2021.08.10.21261726v1 'Without interventions in place, the vast majority of susceptible students among K12 schools will become infected, and school absences will increase, followed by additional cases in communities as infected students transmit to...- bhobba
- Thread
- Delta School
- Replies: 9
- Forum: Biology and Medical
-

I What is the Definition of the Delta Function?
I came across it in the derivation of Gauss' law of electric flux from Coulomb's law. I did some research on it, but the wikipedia page about it was slightly confusing. All I know about it is that it models an instantaneous surge by a distribution. However I am still perplexed by this concept...- Leo Liu
- Thread
- Delta Delta function Dirac Dirac delta Dirac delta function Function
- Replies: 5
- Forum: General Math
-
F
Conservation of charge with Dirac delta
Hello, I was reviewing a part related to electromagnetism in which the charge and current densities are defined by the Dirac delta: ##\rho(\underline{x}, t)=\sum_n e_n \delta^3(\underline{x} - \underline{x}_n(t))## ##\underline{J}(\underline{x}, t)=\sum_n e_n \delta^3(\underline{x} -...- Frostman
- Thread
- Charge Charge density Conservation Conservation of charge Continuity equation Current density Delta Dirac Dirac delta
- Replies: 5
- Forum: Advanced Physics Homework Help
-
A
MHB Proof that lim loga_n/n = 0 in epsilon delta language
Let $\,a>0\,,\,a\neq1\,$ be a real number. We can prove by using the continuity of $\ln n$ function that $\;\lim\limits_{n\to\infty}\dfrac{\log_an}n=0\;$ However, this problem appears in my problems book quite early right after the definition of $\epsilon$-language definition of limit of a... -

COVID Get Vaccinated Against the Covid Delta Variant
Get vaccinated! https://www.yahoo.com/news/the-covid-19-delta-variant-what-you-need-to-know-151035628.html...- Evo
- Thread
- Covid Covid-19 Delta
- Replies: 516
- Forum: Biology and Medical
-
U
A question on the Dirac delta distribution
Is it correct to say that $$\int e^{-i(k+k’)x}\,\mathrm{d}x$$ is proportional to ##\delta(k+k’)##?- user1139
- Thread
- Delta Dirac Dirac delta Dirac delta function Distribution
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
A
Writing the charge density in the form of the Dirac delta function
Hey guys! Sorry if this is a stupid question but I'm having some trouble to express this charge distribution as dirac delta functions. I know that the charge distribution of a circular disc in the ##x-y##-plane with radius ##a## and charge ##q## is given by $$\rho(r,\theta)=qC_a...- approx12
- Thread
- Charge Charge density Delta Delta function Density Dirac Dirac delta Dirac delta function Electrodynamics Form Function Writing
- Replies: 5
- Forum: Advanced Physics Homework Help
-

Is My Delta to Wye Conversion Calculation Correct?
I was following these [steps](https://www.allaboutcircuits.com/textbook/direct-current/chpt-10/delta-y-and-y-conversions/). I was calculating resistance for left side circuit. $$R_1=\frac{2 × 2}{2+2+4}=0.5\Omega$$ $$R_2=\frac{2 × 4}{2+2+4}=1\Omega$$ $$R_3=\frac{2 × 4}{2+2+4}=1\Omega$$ Then...- Istiak
- Thread
- Circuit Delta Resistance Wye
- Replies: 5
- Forum: Introductory Physics Homework Help
-
F
I Understand the delta rule increment in gradient descent
Hello Everyone, I have a question about the gradient descent algorithm. Given a multivariable function ##f(x,y)##, we can find its minima (local or global) by either setting its gradient ##\nabla f = 0## or by using the gradient descent iterative approach. The first approach (setting the... -

I Could this function be approximated by Dirac delta function?
hi, there. I am doing some frequency analysis. Suppose I have a function defined in frequency space $$N(k)=\frac {-1} {|k|} e^{-c|k|}$$ where ##c## is some very large positive number, and another function in frequency space ##P(k)##. Now I need integrate them as $$ \int \frac {dk}{2 \pi} N(k)...- Haorong Wu
- Thread
- Delta Delta function Dirac Dirac delta Dirac delta function Function
- Replies: 2
- Forum: Calculus
-
L
Delta potential problem - bound states problem
I am confused here. For ##x>0## particle is free and for ##x<0## particle is free. That I am not sure how we can have bond states. If particle is in the area ##x>0## why it feel ##\delta## - potential at ##x=0##. Besides that, I know how to solve problem. But I am confused about this. If we...- LagrangeEuler
- Thread
- Bound Bound states Delta Potential States
- Replies: 19
- Forum: Advanced Physics Homework Help
-
L
I Double delta potential -- Degeneracy of bound states in one dimension?
I have a question from the youtube lecture That part starts after 42 minutes and 47 seconds. Balakrishnan said that if delta barriers are very distant (largely separated) then we have degeneracy. I do not understand how this is possible when in 1d problems there is no degeneracy for bond states.- LagrangeEuler
- Thread
- Bound Bound states Degeneracy Delta Dimension Potential States
- Replies: 3
- Forum: Quantum Physics
-

Double Delta Potential: Solving Particle Scattering Problem
Summary:: I have a problem with a particle, which gets scatterd at a double delta-potential Hello, I am really stuck with the floowing problem: A particle moves from the left along the x-axis and gets scatterd at a one-dimensional potential V(x)=a[dirac delta of x) +b [dirac delta of x-c]...- eradan
- Thread
- Delta Delta function Potential Quantum machenics
- Replies: 12
- Forum: Advanced Physics Homework Help
-
M
I Probability: why can we use the Dirac delta function for a conditional pdf?
Hi, I have a quick question about something which I have read regarding the use of dirac delta functions to represent conditional pdfs. I have heard the word 'mask' thrown around, but I am not sure whether that is related or not. The source I am reading from states: p(x) = \lim_{\sigma \to...- Master1022
- Thread
- Conditional Delta Delta function Dirac Dirac delta Dirac delta function Function Pdf Probability
- Replies: 12
- Forum: Set Theory, Logic, Probability, Statistics
-
M
A sudden change in the depth of delta function potential well
is it correct that the continuum states will be free particle states? and the probability will be |< Ψf | ΨB>|^2 . Where Ψf is the wave function for free particle and ΨB is the wave function for the bound state when the depth is B.- Mazhar12
- Thread
- Change Delta Delta function Delta function potential Depth Function Potential Potential well
- Replies: 1
- Forum: Introductory Physics Homework Help
-
A
Chemistry Delta H Calculation: 7.455 + 94 + 8.4
-(7.455 so,94+8,4) Delta T- aname
- Thread
- Delta
- Replies: 5
- Forum: Biology and Chemistry Homework Help
-

I Representations of a delta function
There are many representations of the delta function. Is there a place/reference that lists AND proves them? I am interested in proofs that would satisfy a physicist not a mathematician. -

I Integrating with the Dirac delta distribution
Given \begin{equation} \begin{split} \int_{y-\epsilon}^{y+\epsilon} \delta^{(2)}(x-y) f(x) dx &= f^{(2)}(y) \end{split} \end{equation} where ##\epsilon > 0## Is the following also true as ##\epsilon \rightarrow 0## \begin{equation} \begin{split} \int_{y-\epsilon}^{y+\epsilon}...- redtree
- Thread
- Delta Derivative Dirac Dirac delta Distribution Integral Interval
- Replies: 9
- Forum: Differential Equations
-
Z
Delta function for \nabla(log s), where s = \sqrt{x^2+y^2}
My intuition for this problem is to use divergence theorem: ## \int_V \nabla^2 u dV = \int_S \nabla u \cdot \vec{n} dS## But note that ##\vec{n}## is perpendicular to x-y plane, and makes ##\int_S \nabla \ln s \cdot \vec{n} dS = 0## If we take laplacian in polar coordinate directly, then...- zhuang382
- Thread
- Delta Delta function Function
- Replies: 2
- Forum: Advanced Physics Homework Help
-

A Dirac delta function confusion
As a part of a bigger problem, I was trying to evaluate the D'Alambertian of ##\epsilon(t)\delta(t^2-x^2-y^2-z^2)##, where ##\epsilon(t)## is a sign function. This term appears in covariant commutator function, so I was checking whether I can prove it solves Klein-Gordon equation. Since there's... -

MHB Dirac Delta and Fourier Series
A beam of length L with fixed ends, has a concentrated force P applied in the center exactly in L / 2. In the differential equation: \[ \frac{d^4y(x)}{dx^4}=\frac{1}{\text{EI}}q(x) \] In which \[ q(x)= P \delta(x-\frac{L}{2}) \] P represents an infinitely concentrated charge distribution...- rannasquaer
- Thread
- Delta Dirac Dirac delta Fourier Fourier series Series
- Replies: 2
- Forum: General Math
-

MHB How do I find the value of delta in a delta epsilon proof using a graph?
Find a graph to a number $\delta$ such that $$\textit{if } |x-1|<\delta \textit{ then } \left|\dfrac{2x}{x^2+4}-0.4\right|<0.1 $$ ok I always had a very hard time doing these I did look at some examples but still ? did a ibispaint drawing to start basically it looks like we are finding the... -

Product of two Kronecker delta symbols as a determinant
I don't have a clue as to how to go about proving (or verifying) the equation above. It would be very hard to take individual values of i,j and k and p,q and r for each side and evaluate ##3^6## times! More than that, I'd like a proof more than a verification. Any help would be welcome.- brotherbobby
- Thread
- Delta Determinant Product Symbols
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
C
A Evaluation of an improper integral leading to a delta function
Hi, I have pasted two improper integrals. The text has evaluated these integrals and come up with answers. I wanted to know how these integrals have been evaluated and what is the process to do so. Integral 1 Now the 1st integral is again integrated Now the text accompanying the integration...- chiraganand
- Thread
- Delta Delta function Function Improper integral Integral
- Replies: 3
- Forum: Calculus
-

I Is the Kronecker Delta Calculation in Peskin and Schroeder's Solution Correct?
My problem is on page 194 of the solution, where he writes: ##\frac{1}{2}\delta^{ab}\frac{1}{2}\delta^{ab}=2##. I assume there are three colours and thus ##a,b \in \{ 0,1,2 \}##. So I get: ##\delta^{ab}\delta^{ab} =...- MathematicalPhysicist
- Thread
- Book Delta Final Project
- Replies: 6
- Forum: Quantum Physics
-
P
Neural Networks Question about the Hebbs and Delta Rule
Good afternoon, I am currently working on Neural Networks and I am reading an introduction by Jeff Heaton (Neural Networks in Java). Now there are two tasks there whose solutions interest me. The first task is about applying the Hebbs rule. In the book it is given wrong because of a typo but I...- Peter_Newman
- Thread
- Delta Networks Neural Neural networks
- Replies: 1
- Forum: Programming and Computer Science
-
G
Integral Involving the Dirac Delta Function
- gabriellelee
- Thread
- Delta Delta function Dirac Dirac delta Dirac delta function Function Integral
- Replies: 13
- Forum: Advanced Physics Homework Help
-
M
Kronecker Delta & Levi Civita manipulation
εikl εjmngkmMkn = εikl εjknMkn = (in book it changed sign to -εikl εjknMkn - Why? ) By identity εikl εnjkMln = (δinδkj - δijδkn)Mkn = ? I then get .. Mji - δij Mnn ( is this correct ?) There 's more to the question but if can get this part right, I should be able to complete the...- MichaelAlexDavM
- Thread
- Delta Levi-civita Manipulation
- Replies: 7
- Forum: Advanced Physics Homework Help
-
A Delta Baryon Quartet: Constructing from SU(2) Symmetry
In ##SU(2)## symmetry, we can define a triplet as ##2\otimes 2^*=3\oplus 1## with a tensor representation like this: $$q_iq_j^*=\left(q_iq^j-\frac{1}{2}\delta_j^iq_kq^k\right)+\frac{1}{2}\delta_j^iq_kq^k.$$ The upper index denotes an anti-doublet and the traceless part in parentheses represents...- lalo_u
- Thread
- Delta
- Replies: 1
- Forum: High Energy, Nuclear, Particle Physics
-
N
Chemistry Calculating delta H of reaction using bond energies?
Hi, I have been stuck for hours, i do not understand how i am supposed to use bond energy values for this question like it asks when bond energy values are for molecules in the gas state. The first molecule reactant is a liquid and the second reactant has resonance. I have 0 idea how to approach...- needhelpwithchem
- Thread
- Bond Delta Energies Reaction
- Replies: 2
- Forum: Biology and Chemistry Homework Help
-
J
Scattering amplitude in scattering from a delta function
I tried to calculate the Fourier transform to get the amplitude, but I got lost- joaosantossilva
- Thread
- Amplitude Delta Delta function Function Scattering
- Replies: 1
- Forum: Advanced Physics Homework Help
-

Engineering Dirac Delta Function in an Ordinary Differential Equation
1.) Laplace transform of differential equation, where L is the Laplace transform of y: s2L - sy(0) - y'(0) + 9L = -3e-πs/2 = s2L - s+ 9L = -3e-πs/2 2.) Solve for L L = (-3e-πs/2 + s) / (s2 + 9) 3.) Solve for y by performing the inverse Laplace on L Decompose L into 2 parts: L =...- giveortake
- Thread
- Delta Delta function Differential Differential equation Dirac Dirac delta Dirac delta function Function Ordinary differential equation
- Replies: 3
- Forum: Engineering and Comp Sci Homework Help