Interval Definition and 712 Threads

In music theory, an interval is a difference in pitch between two sounds.
An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.In Western music, intervals are most commonly differences between notes of a diatonic scale. The smallest of these intervals is a semitone. Intervals smaller than a semitone are called microtones. They can be formed using the notes of various kinds of non-diatonic scales. Some of the very smallest ones are called commas, and describe small discrepancies, observed in some tuning systems, between enharmonically equivalent notes such as C♯ and D♭. Intervals can be arbitrarily small, and even imperceptible to the human ear.
In physical terms, an interval is the ratio between two sonic frequencies. For example, any two notes an octave apart have a frequency ratio of 2:1. This means that successive increments of pitch by the same interval result in an exponential increase of frequency, even though the human ear perceives this as a linear increase in pitch. For this reason, intervals are often measured in cents, a unit derived from the logarithm of the frequency ratio.
In Western music theory, the most common naming scheme for intervals describes two properties of the interval: the quality (perfect, major, minor, augmented, diminished) and number (unison, second, third, etc.). Examples include the minor third or perfect fifth. These names identify not only the difference in semitones between the upper and lower notes but also how the interval is spelled. The importance of spelling stems from the historical practice of differentiating the frequency ratios of enharmonic intervals such as G–G♯ and G–A♭.

View More On Wikipedia.org
Recent contents Top users
  1. S

    Find interval and root of polynomial with absolute error less than 1/8

    By IVT and trial and error, I get the interval to be ##(-\frac{1}{2},-\frac{1}{4})## I don't know how to do the next part. Let the actual root of the polynomial be ##x_{0}## and the approximate value is ##p##, we have ##|p-x_{0}|<\frac{1}{8}## I am not sure how to continue. Thanks
  2. L

    Proving a statement about covered intervals

    I need any idea. I haven't made any progress in solving the problem.
  3. Hak

    I Time intervals measured by stationary and moving observers

    [Moderator's note: Thread moved to relativity forum as it is not a specific homework problem but a general question about SR.] Homework Statement: While studying relativity, a question arose for me about time intervals measured by stationary and moving observers. In particular, one of the...
  4. M

    Is it possible to find a number x such that 5 < x < 1?

    I don't think it is possible, but can someone please explain why? Many thanks!
  5. F

    I When can Ordinal Variables be treated as Interval Variables?

    Hello, Ordinal variables (see Likert scale) can be labelled using numbers and ranked by those numbers. However, the difference between category 2 and category 3 may not be exactly be the same as the difference between category 4 and 5. That said, I noticed that in social science ordinal...
  6. Euge

    POTW Fourier Series on the Unit Interval

    Evaluate the Fourier series $$\frac{1}{\pi^2}\sum_{k = 1}^\infty \frac{\cos 2\pi kx}{k^2}$$ for ##0 \le x \le 1##.
  7. M

    Proving g(x) is continuous over interval (-∞,-2)

    For number 18, The solution is, However, should they not write "For ## -∞ < a < -2##" since ##a ≠ -∞## (infinity is not a number)? Many thanks!
  8. V

    B Collision time interval of a gas molecule with wall of container

    I have been trying to make sense of the derivation of pressure under Kinetic Theory of Gases chapter, but it's not making sense to me when the impulse momentum equation is used for the collision between a gas molecule and the wall of the container. The book says that for the elastic collision...
  9. K

    I Proper Time Interval: Exploring its Definition on Wikipedia

    Wikipedia article on proper time "Given this differential expression for ##\tau##, the proper time interval is defined as ## \Delta \tau=\int_P d \tau=\int \frac{d s}{c} . ## Here ##P## is the worldline from some initial event to some final event with the ordering of the events fixed by the...
  10. chwala

    Find a 95% confidence interval for population mean

    I am refreshing on this... I think there is a mistake on the circled part in red...right? not correct symbol for sample mean...This is the part that i need clarity on. The other steps to solution are pretty easy to follow...as long as one knows the t-formula and also the knowledge to...
  11. H

    I Spacetime interval and basic properties of light

    While not having a professional physics background I was still interested in knowing more about special and general relativity. Therefore I was trying to find out where the space time interval was coming from in relation to the speed of light. Of course this is the first point to start I...
  12. junyoung

    I Open interval or Closed interval in defining convex function

    The Korean textbook standard defines the convexity of the function as an open section. Many textbooks and university calculus textbooks define the convexity of the curve as an open section. However, some textbooks define convexity as closed sections. Do you think it is right to define the...
  13. ilasus

    Determining the interval between two F1 cars

    Two cars A, B move in the same direction with the constant speeds v, u (v < u) on a rectilinear OM circuit, specially built for Formula 1 cars. Assuming that at the initial moment (t = 0), the two cars are on the starting line O (x = 0) of the OM circuit and that, during t, the cars A, B travel...
  14. S

    Correct statement related to confidence interval

    I think (e) is wrong because the proportion should be out of the whole population, not only in a certain class and option (a) to (d) looks like identical to me so I answered (a), (b), (c) and (d) but my answer is wrong. Where is my mistake? Thanks
  15. K

    I Probability in a small interval is ##P. dx##

    Reif says " ... variable ##u## which can assume any value in the continuous range ##a_{1}<u<a_{2}##. To give a probability description of such a situation, one can focus attention on any infinitesimal range of the variable between ##u## and ##u+d u## and ask for the probability that the variable...
  16. M

    MHB Show that C gives a confidence interval for θ

    Hey! 😊 For $n \in \mathbb{N}$ we consider the discrete statistical product model $(X, (\mathbb{P}_{\theta})_{\theta\in \Theta})$ with $X=\mathbb{N}^n$, $\Theta=\mathbb{N}$ and $p_{\theta}(x_i)=\frac{1}{\theta}1_{\{1\leq x_i\leq \theta\}}$ forall $x_i\in \mathbb{N}$, $\theta\in \Theta$. Let...
  17. M

    MHB Determine the confidence interval

    Hey! 😊 (a) In winter, the roads around Lake Macatawa are salted. To study the impact of this on Lake Macatawa, students took $32$ water samples from the western basin of the lake and Sodium content (in parts per million, ppm) determined. As a result, the students have receive the following...
  18. T

    A Existence of unique solutions to a first order ODE on this interval

    I am trying to find a way to prove that a certain first order ode has a unique solution on the interval (1,infinity). Usually the way to do this is to show that if x' = f(t,x) (derivative with respect to t), then f(t,x) and the partial derivative with respect to f are continuous. However, this...
  19. A

    Changing the interval of integration

    Greetings Dear community! Here is the solutions using two different methods: the first method is the Green theorem and the second is the simple path integration method: My question is why they integrate over [0.2pi] in the path integration method while they integrate within [0. pi] in the...
  20. msrultons

    Find the largest interval on which f is increasing

    Attached here is the full problem I am doing. I went through the problem and got my final answer which I thought was correct. Here is my work. They tell me I am wrong. Not sure where is the mistake.
  21. Monsterboy

    Zero velocity for a time interval, what about acceleration?

    For a particle moving in a straight line, if the velocity is zero for a time interval, the acceleration is zero at any instant within the time interval. I am told the above statement is true. If I look at the equations v = dx/dt a = dv/dt It looks like if the velocity is zero for a time...
  22. M

    MHB Confidence interval of difference

    Hey! :giggle: From two populations of small and medium enterprises, we collect two random and independent samples of size $n_1 = 64$ and $n_2 = 36$ enterprises respectively. If we calculate for the companies of the first sample average sales of $9$ thousand euros and a variation of $4$, while...
  23. LCSphysicist

    Special relativity - Trivial exercise with spacetime interval

    For a observer on Earth, a rocket takes Mike from Earth to Pluto with a speed of 0.82 c for 33.72 yr. Find the space-time interval for the two events such as Mike leaving the Earth and reaching Pluto considering Pluto is at rest relative to Earth for the observer on Earth. I confess that i am...
  24. Demystifier

    I An open set can be a closed interval?

    I am confused with some basic definitions in general topology. Topological space is defined as a set ##X## and a collection ##T## of its subsets that satisfies some general properties (which I will not list here, but I will assume that the reader knows them). But such a very general definition...
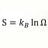
  25. morrobay

    B Time like spacetime interval, proper time, and time dilation

    Since the time like spacetime interval is equal to proper time for stationary or traveling observers, then it seems time dilation (proper time) seen with traveling clock is necessarily frame invariant. Then the so called time between ticks of both identical clocks, with stationary and traveling...
  26. karush

    MHB -apc.2.1.06 crosses the x-axis at one point in the interval [0,1]

    $\tiny{APC.2.1.06}$ The graph of $y=e^{\tan x}-2$ crosses the x-axis at one point in the interval [0,1] What is the slope of the graph at this point. a, 0.606 b. 2 c, 2.242 d.2.961 e.3.747 [d] $\begin{array}{rll} \textit{given} &e^{\tan \:x}-2 &(1)\\...
  27. greg_rack

    B Definition of Spacetime Interval

    Hi guys, I'll attach an excerpt from my textbook which isn't, in my opinion, very clear in explaining a spacetime interval(or I'm just missing the key to get the concept). "How do we combine two different measurements such as time and space, to form an invariant variable? We can simply write...
  28. G

    I Exploring Spacetime Interval at a Singularity: Tad Williams' Otherland

    Tad Williams’ Otherland series has a scene where the characters are drawn to a temple no matter which direction they try to walk, as if space itself is curved. This is kind of the intuition I get when a physicist talks about the spacetime interval kind of flipping past an event horizon: if you...
  29. L

    MHB Is an increasing monotonic function in a closed interval also continuous?

    Hello all, Is this statement true ? Is every increasing monotonic function in a closed interval also continuous ? How do you prove such a thing ? Thank you !
  30. G

    MHB Interval of the Riemann integral value

    Hello everyone, I have to find an interval of this Riemann integral. Does anybody know the easiest way how to do it? I think we need to do something with denominator, enlarge it somehow. My another guess is the integral is always larger than 0 (A=0) because the whole function is still larger...
  31. redtree

    I Integrating with the Dirac delta distribution

    Given \begin{equation} \begin{split} \int_{y-\epsilon}^{y+\epsilon} \delta^{(2)}(x-y) f(x) dx &= f^{(2)}(y) \end{split} \end{equation} where ##\epsilon > 0## Is the following also true as ##\epsilon \rightarrow 0## \begin{equation} \begin{split} \int_{y-\epsilon}^{y+\epsilon}...
  32. karush

    MHB -2.4.2 interval of initial value problem

    Determine an interval in which the solution of the given initial value problem is certain to exist $t(t-4)y'+y=0 \quad y(2)=2\quad 0<t<4$ ok my first step was isolate y' s $y'=-\dfrac{y}{t(t-4)}$ not sure what direction to go since we are concerned about an interval
  33. karush

    MHB 3.3.2 AP Calculus Exam interval from f'(x)

    screen shot to avoid typos OK the key said it was D I surfed for about half hour trying to find a solution to this but $f'(0)$ doesn't equal any of these numbers $e^0=\pm 1$ from the $e^{(x^2-1)^2}$ kinda ?
  34. S

    Do Other Musical Intervals Create a Creepy Sound Like the Devil's Interval?

    Are there other intervals that do what this one does? I poked around briefly on a guitar to try to check another couple of oddball chords to see which intervals were making it sound odd, but I could not see a match to any augmented 4th. (the kind of tones or NOTES combined which make music...
  35. Mayhem

    I Separation of Variables and Integrating over an Interval

    I was solving the van't Hoff equation over an interval ##[T_1 , T_2]##: The van't Hoff equation ## \frac{\mathrm{d} \ln K}{\mathrm{d} T} = \frac{\Delta_r H^{\circ}}{RT^2} ## which can be solved with separation of variables: ## d \ln K = \frac{\Delta_rH^\circ}{RT^2}dT ## ##\Updownarrow##...
  36. G

    How Do I Calculate Confidence Intervals for Two Means?

    Here is the question I'm struggling with (Q1) : I just... I just don't understand what my first step is. Whats my barx1 and barx2? (bar x = mean, x1 = subscript 1) My thoughts on approaching this question : barX1 - barX2 `~ N(u1-u2, sd1^2/n1 + sd2^2/n2) Find Z value when p = 0.975, z = + or...
  37. Math Amateur

    MHB Outer measure of an open interval ....

    I am reading Sheldon Axler's book: Measure, Integration & Real Analysis ... and I am focused on Chapter 2: Measures ... I need help with proving that the outer measure of an open interval, \mid (a, b) \mid = b - a Axler's definitions of length and outer measure are as follows: Can someone...
  38. rxh140630

    Determining if a number is within an interval

    0<k<1 x<y x,y \in {[a,b]} a,b \in {\mathbb R} Question: is yk + (1-k)x \in {[a,b]} My response: yk + (1-k)y = y Since x<y, yk + (1-k)x < y xk + (1-k)x = x Since y>x , yk + (1-k)x > x Therefore x < yk + (1-k)x < y, so yk + (1-k)x is in the interval [a,b] Is this considered...
  39. Math Amateur

    I Outer measure of a closed interval .... Axler, Result 2.14 ....

    I am reading Sheldon Axler's book: Measure, Integration & Real Analysis ... and I am focused on Chapter 2: Measures ... I need help with the proof of Result 2.14 ... Result 2.14 and its proof read as follows: In the above proof by Axler we read the following: " ... ... We will now prove by...
  40. Math Amateur

    MHB Outer measure of a closed interval .... Axler, Result 2.14 ....

    I am reading Sheldon Axler's book: Measure, Integration & Real Analysis ... and I am focused on Chapter 2: Measures ... I need help with the proof of Result 2.14 ... Result 2.14 and its proof read as follows: In the above proof by Axler we read the following: " ... ... We will now prove by...
  41. M

    A Can the Unit Interval be Measurably Split into Two Sets of Equal Length?

    Can the unit interval be split into two measurable sets (A and B each measure 1/2), so that for any sub-interval [c,d] the intersections ##A\cap [c,d]## and ##B\cap [c,d]## each measure half the length of [c,d]? I doubt it, but I would like to see a proof, one way or the other.
  42. Adesh

    I Will ##M_i = m_i## if an interval is made vanishingly small?

    We define : $$M_i = sup \{f(x) : x \in [x_{i-1}, x_i ] \}$$ $$m_i = inf \{f(x) : x \in [ x_{i-1}, x_i ] \}$$ Now, if we make the length of the interval ##[x_{i-1}, x_i]## vanishingly small, then would we have ##M_i = m_i##? I have reasons for believing so because as the size of the interval is...
  43. iVenky

    I Confidence interval on Standard deviation

    I read that confidence interval on standard deviation can be found using chi-square distribution. If I have a sample size N=500, and sample standard deviation= 3 with mean=0, and I need a 95% confidence, I wasn't sure what to set for degrees of freedom in chi-square formula. Is the degrees of...
  44. WMDhamnekar

    MHB Increasing and decreasing interval of this function |e^x+e^{-x}|

    Hello, I want to know what is the incresing and decreasing interval of this even function $|e^x+e^{-x}|?$ If any member knows the correct answer, may reply to this question.
  45. A

    Time interval between intermediate passing of two rods....

    The first part I have calculated is as follows:: Length of A seen by S =30m Length of B seen by S=40m In S frame, Time for front of A and B to come in same line 0.8ct=40+0.6ct...t=200/c From the above position time for back end of A and front of B to come in same line 0.8ct=30+0.6ct...t=150...
  46. MattGeo

    I Spacetime Interval & Energy-Momentum 4Vec: Reconciling Hyperbolic Geometry

    In a spacetime diagram the spatialized time direction is the vertical y-axis and the pure space direction is the horizontal x-axis, ct and x, respectively. The faster you go and therefore the more kinetic energy you have, you'll have a greater component of your spacetime vector in the...
  47. LCSphysicist

    Exploring the TL Interval Square Measurement

    I was reading about the general theory of relativity, and came to a chapter that the author start to talk about an invariant measurement by [TL] named interval square. It's the first time that i read about it, and i don't get it yet. An event, what he is calling, is anything? If I am thinking...
  48. evinda

    MHB Interval with Dirac function in a finite interval

    Hello! (Wave) I want to calculate the integral $\int_{-1}^2\sin \left (\pi (t-1)\right )\delta (-t+1)\, dt$. I have done the following so far: $$\int_{-\infty}^{+\infty}\sin \left (\pi (t-1)\right )\delta (-t+1)\, dt=\int_{-\infty}^1\sin \left (\pi (t-1)\right )\delta (-t+1)\...
  49. naushaan

    Calculating average acceleration during a time interval

    Here's my calculations for (a) and (b)
  50. F

    Find the interval of convergence of this power series

    ∑((√(x2+1))n22/(3n+n3)) We use the ratio test: ρn = |2(3n+n3)√(x2+1)/(3n+1+(n+1)3)| ρ = |2√(x2+1)| ρ < 1 |2√(x2+1)| < 1 No "x" satisfies this expression, so I conclude the series doesn't converge for any "x". However the answer in the book says the series converges for |x| < √(5)/2. What am...
Back
Top