Delta function Definition and 379 Threads

In mathematics, the Dirac delta function (δ function) is a generalized function or distribution, a function on the space of test functions. It was introduced by physicist Paul Dirac. It is called a function, although it is not a function R → C.
It is used to model the density of an idealized point mass or point charge as a function equal to zero everywhere except for zero and whose integral over the entire real line is equal to one. No function has these properties, such that the computations made by theoretical physicists appeared to mathematicians as nonsense until the introduction of distributions by Laurent Schwartz to formalize and validate the computations. As a distribution, the Dirac delta function is a linear functional that maps every function to its value at zero. The Kronecker delta function, which is usually defined on a discrete domain and takes values 0 and 1, is a discrete analog of the Dirac delta function.
In engineering and signal processing, the delta function, also known as the unit impulse symbol, may be regarded through its Laplace transform, as coming from the boundary values of a complex analytic function of a complex variable. The convolution of a (theoretical) signal with a Dirac delta can be thought of as a stimulation that includes all frequencies. This leads to a resonance with the signal, making the theoretical signal "real" (i.e. causal). The formal rules obeyed by this function are part of the operational calculus, a standard tool kit of physics and engineering. In many applications, the Dirac delta is regarded as a kind of limit (a weak limit) of a sequence of functions having a tall spike at the origin (in theory of distributions, this is a true limit). The approximating functions of the sequence are thus "approximate" or "nascent" delta functions.

View More On Wikipedia.org
Recent contents Top users
  1. M

    A Going from Kronecker deltas to Dirac deltas

    I'm reading Stefanucci's Nonequilibrium Many Body Theory of Quantum Systems. In the first chapter, where it goes over basic quantum mechanics, it first defines the usual orthonormality condition I'm familiar with, $$\langle n' | n \rangle = \delta_{n, n'} $$ where $$ | n \rangle$$ is the ket...
  2. Z

    Understanding calculation of 2nd order LTI DE response to step input

    This question is based on the calculations in these notes on 2nd order unit step response. Some Initial Observations The scenario modeled here is an undamped spring-mass system that is at rest until time ##0##, at which point a constant force starts to act on the mass. The force is finite and...
  3. L

    Dirac delta function approximation

    Hi, I'm not sure if I have calculated task b correctly, and unfortunately I don't know what to do with task c? I solved task b as follows ##\displaystyle{\lim_{\epsilon \to 0}} \int_{- \infty}^{\infty} g^{\epsilon}(x) \phi(x)dx=\displaystyle{\lim_{\epsilon \to 0}} \int_{\infty}^{\epsilon}...
  4. yucheng

    I Fermi's golden rule: why delta function instead of density states?

    Sakurai, in ##\S## 5.7.3 Constant Perturbation mentions that the transition rate can be written in both ways: $$w_{i \to [n]} = \frac{2 \pi}{\hbar} |V_{ni}|^2 \rho(E_n)$$ and $$w_{i \to n} = \frac{2 \pi}{\hbar} |V_{ni}|^2 \delta(E_n - E_i)$$ where it must be understood that this expression is...
  5. H

    Kramers-Kronig, parity and delta function

    Hi, First of all, I'm not sure to understand what he Kramers-kronig do exactly. It is used to get the Real part of a function using the imaginary part? Then, when asked to add a peak to the parity at ##\omega = -\omega_0##, is ##Im[\epsilon_r(\omega)] = \delta(\omega^2 - \omega_0 ^2)## correct...
  6. P

    A Time dependent problem with a delta function

    Hello, I try to solve a time dependent problem described by a Hamiltonian of the type $$ \mathcal{H}(t) = H_0 + V \delta(t) .$$ I started by trying to solve the Schrödinger equation with ##H_0 = p^2 / 2m##, but I'm getting a bit stuck. I would like to know if you know of any books that deal...
  7. H

    Mellin transform of Dirac delta function ##\delta(t-a)##

    Hi, I found Laplace transform of this Dirac delta function which is ##F(s) = e^{-st}## since ##\int_{\infty}^{-\infty} f(t) \delta (t-a) dt = f(a)## and that ##\delta(x) = 0## if ##x \neq 0## Then the Mellin transform ##f(t) = \frac{1}{2 \pi i} \int_{\gamma - i \omega}^{\gamma +i \omega}...
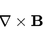
  8. anaisabel

    Delta function to calculate density of probablity

  9. Leo Liu

    I What is the Definition of the Delta Function?

    I came across it in the derivation of Gauss' law of electric flux from Coulomb's law. I did some research on it, but the wikipedia page about it was slightly confusing. All I know about it is that it models an instantaneous surge by a distribution. However I am still perplexed by this concept...
  10. A

    Writing the charge density in the form of the Dirac delta function

    Hey guys! Sorry if this is a stupid question but I'm having some trouble to express this charge distribution as dirac delta functions. I know that the charge distribution of a circular disc in the ##x-y##-plane with radius ##a## and charge ##q## is given by $$\rho(r,\theta)=qC_a...
  11. Haorong Wu

    I Could this function be approximated by Dirac delta function?

    hi, there. I am doing some frequency analysis. Suppose I have a function defined in frequency space $$N(k)=\frac {-1} {|k|} e^{-c|k|}$$ where ##c## is some very large positive number, and another function in frequency space ##P(k)##. Now I need integrate them as $$ \int \frac {dk}{2 \pi} N(k)...
  12. eradan

    Double Delta Potential: Solving Particle Scattering Problem

    Summary:: I have a problem with a particle, which gets scatterd at a double delta-potential Hello, I am really stuck with the floowing problem: A particle moves from the left along the x-axis and gets scatterd at a one-dimensional potential V(x)=a[dirac delta of x) +b [dirac delta of x-c]...
  13. M

    I Probability: why can we use the Dirac delta function for a conditional pdf?

    Hi, I have a quick question about something which I have read regarding the use of dirac delta functions to represent conditional pdfs. I have heard the word 'mask' thrown around, but I am not sure whether that is related or not. The source I am reading from states: p(x) = \lim_{\sigma \to...
  14. M

    A sudden change in the depth of delta function potential well

    is it correct that the continuum states will be free particle states? and the probability will be |< Ψf | ΨB>|^2 . Where Ψf is the wave function for free particle and ΨB is the wave function for the bound state when the depth is B.
  15. Frabjous

    I Representations of a delta function

    There are many representations of the delta function. Is there a place/reference that lists AND proves them? I am interested in proofs that would satisfy a physicist not a mathematician.
  16. Z

    Delta function for \nabla(log s), where s = \sqrt{x^2+y^2}

    My intuition for this problem is to use divergence theorem: ## \int_V \nabla^2 u dV = \int_S \nabla u \cdot \vec{n} dS## But note that ##\vec{n}## is perpendicular to x-y plane, and makes ##\int_S \nabla \ln s \cdot \vec{n} dS = 0## If we take laplacian in polar coordinate directly, then...
  17. Antarres

    A Dirac delta function confusion

    As a part of a bigger problem, I was trying to evaluate the D'Alambertian of ##\epsilon(t)\delta(t^2-x^2-y^2-z^2)##, where ##\epsilon(t)## is a sign function. This term appears in covariant commutator function, so I was checking whether I can prove it solves Klein-Gordon equation. Since there's...
  18. E

    S-wave phase shift for quantum mechanical scattering

    a.) The potential is a delta function, so ##V \left( r \right) = \frac {\hbar^2} {2\mu} \gamma \delta \left(r-a \right)##, therefore ##V \left( r \right) = \frac {\hbar^2} {2\mu} \gamma ## at ##r=a##, and ##V \left( r \right) = 0## otherwise. I've tried a few different approaches: 1.) In...
  19. C

    A Evaluation of an improper integral leading to a delta function

    Hi, I have pasted two improper integrals. The text has evaluated these integrals and come up with answers. I wanted to know how these integrals have been evaluated and what is the process to do so. Integral 1 Now the 1st integral is again integrated Now the text accompanying the integration...
  20. G

    Integral Involving the Dirac Delta Function

  21. J

    Scattering amplitude in scattering from a delta function

    I tried to calculate the Fourier transform to get the amplitude, but I got lost
  22. giveortake

    Engineering Dirac Delta Function in an Ordinary Differential Equation

    1.) Laplace transform of differential equation, where L is the Laplace transform of y: s2L - sy(0) - y'(0) + 9L = -3e-πs/2 = s2L - s+ 9L = -3e-πs/2 2.) Solve for L L = (-3e-πs/2 + s) / (s2 + 9) 3.) Solve for y by performing the inverse Laplace on L Decompose L into 2 parts: L =...
  23. Arman777

    Solve $$\int_{∞}^{∞}dxf(x)\delta((x-x_1))$$: Dirac Delta Function

    If the question was $$ \int_{∞}^{∞}dxf(x)δ((x - x_1)) = ? $$ The answer would be ##f(x_1)## So the delta function has two roots, I searched the web and some books but I am not sure what approach should I use here. I guess there's sometihng happens when ##x_1 = -x_2##. So I am not sure what...
  24. JorgeM

    I Is this Dirac delta function integral correct?

    I have to integrate this expression so I started to solve the delta part from the fact that when n=0 it results equals to 1. And the graph is continuous in segments I thought as the sumation of integers $$ \int_{-(n+1/2)π}^{(n+1/2)π} δ(sin(x)) \, dx $$ From the fact that actually $$ δ(sin(x))=...
  25. amjad-sh

    Dirac delta function of a function of several variables

    Form solid state physics, we know that the volume of k-space per allowed k-value is ##\triangle{\mathbf{k}}=\dfrac{8\pi^3}{V}## ##\sum_{\mathbf{k}}F(\mathbf{k})=\dfrac{V}{(2\pi)^3}\sum_{\mathbf{k}}F(\mathbf{k})\triangle{\mathbf{k}}##...
  26. Alan Lins Alves

    Problem with the Finite Element Method applied to Electrostatics

    Hi! I have a code that solve the poisson equation for FEM in temperature problems. I tested the code for temperature problems and it works! Now i have to solve an Electrostatic problem. There is the mesh of my problem (img 01). At the left side of the mesh we have V=0 (potencial). There is a...
  27. Teri

    Differential equation - delta function

    Moved from technical math section, so is missing the homework template. How to solve this equation please? I found charakteristic roots ia ##\pm \sqrt{-a^{-k^2}}##. Thank you Moderator note: Edited the LaTeX above to show the exponent correctly.
  28. D

    Energy Difference with a Two Delta Function Potential

    Homework Statement Consider a particle of mass m moving in a one-dimensional double well potential $$V(x) = -g\delta(x-a)-g\delta(x+a), g > 0$$ This is an attractive potential with ##\delta##-function dips at x=##\pm a##. In the limit of large ##\lambda##, find a approximate formula for the...
  29. R

    Trying to solve a 2nd order diffy-Q with delta function

    My function: d2f/dx2 + cf = delta(x) Condition: f is finite and f(50) = f(-50) = 0 Solution: f = C1exp(cx) + C2exp(-cx) Due to condition, f = C1exp(cx) for x<=0 and C2exp(-cx) for x>=0 f(50) = C2exp(-c*50) = 0 = > C2 = 0 Likewise, for C1 I don't know if I might have missed something...
  30. P

    I Is the derivative of a discontinuity a delta function?

    In these notes, https://ocw.mit.edu/courses/physics/8-04-quantum-physics-i-spring-2016/lecture-notes/MIT8_04S16_LecNotes10.pdf, at the end of page 4, it is mentioned: (3) V(x) contains delta functions. In this case ψ'' also contains delta functions: it is proportional to the product of a...
  31. Telemachus

    Correct numerical modeling of the 3D Dirac Delta function

    Hi. I was trying to test a code for the diffusion equation, using the analytical solution for infinite media, with a Dirac delta source term: ##q(\mathbf{r},t)=\delta (\mathbf{r}) \delta (t)##. The code is not giving the analytical solution, and there might be several reasons why this is so...
  32. D

    I Show that the integral of the Dirac delta function is equal to 1

    Hi, I am reading the Quantum Mechanics, 2nd edition by Bransden and Joachain. On page 777, the book gives an example of Dirac delta function. $\delta_\epsilon (x) = \frac{\epsilon}{\pi(x^2 + \epsilon^2)}$ I am wondering how I can show $\lim_{x\to 0+} \int_{a}^{b} \delta_\epsilon (x) dx$...
  33. P

    Calculate the Dirac delta function integral

    https://1drv.ms/w/s!Aip12L2Kz8zghV6Cnr8jPcRTpqTX https://1drv.ms/w/s!Aip12L2Kz8zghV6Cnr8jPcRTpqTX My question is in the above link
  34. S

    I Question about the Dirac delta function

    Hi, if I have an interval on the x-axis, defined by the parameter L, can this, interval be transformed to a Dirac delta function instead, on the x-axis? Thanks!
  35. I

    I Meaning of Dirac Delta function in Quantum Mechanics

    If I have a general (not a plain wave) state $$|\psi\rangle$$, then in position space : $$\langle \psi|\psi\rangle = \int^{\infty}_{-\infty}\psi^*(x)\psi(x)dx$$ is the total probability (total absolute, assuming the wave function is normalized) So if the above is correct, does that mean...
  36. Milsomonk

    Integrating a delta function of a function

    Homework Statement Evaluate the integral: $$\int_{-\infty}^{\infty} dx *\dfrac {\delta (x^2-2ax)} {x+b}$$ Homework Equations $$ x^2-2ax=0 $$ The Attempt at a Solution I know that the delta function can only be none zero when $$ x=2a$$ so then I have the following integral...
  37. RJLiberator

    Valid Representation of Dirac Delta function

    Homework Statement Show that this is a valid representation of the Dirac Delta function, where ε is positive and real: \delta(x) = \frac{1}{\pi}\lim_{ε \rightarrow 0}\frac{ε}{x^2+ε^2} Homework Equations https://en.wikipedia.org/wiki/Dirac_delta_function The Attempt at a Solution I just...
  38. gimak

    How Does the Delta Function and Its Derivative Interact with Shifted Functions?

    Homework Statement Prove the following '()( − ) = −′() ∫-∞∞δ'(x)*f(x-a) = -f'(a) Homework Equations ∫-∞∞δ'(x-a)*f(x) = f(a) The Attempt at a Solution [/B] ∫-∞ ∞δ'(x)*f(x-a) = ∫δ(x)*f(x-a)dx-∫f'(x-a)*δ(x)dx = f(-a) - f'(-a) Went from 1st to second by integration by parts Used...
  39. Tbonewillsone

    Recovering the delta function with sin⁡(nx)/x

    Homework Statement Ultimately, I would like a expression that is the result of an integral with the sin(nx)/x function, with extra terms from the expansion. This expression would then reconstruct the delta function behaviour as n goes to infty, with the extra terms decaying to zero. I...
  40. H

    I Square of Dirac delta function

    Is the square of a Dirac delta function, ##(\delta(x))^2##, still a Dirac delta function, ##\delta(x)##? A Dirac delta function peaks at one value of ##x##, say 0. If it is squared, it still peaks at the same value, so it seems like the squared Dirac delta function is still a Dirac delta...
  41. Pushoam

    Dirac delta function in spherical cordinates

    Homework Statement Calculate ##\int_{r=0}^\inf δ_r (r -r_0)\,dr## Homework Equations ##\int_V \delta^3(\vec{r} - \vec{r}') d\tau = 1## The Attempt at a Solution $$\int_V \delta^3(\vec{r} - \vec{r}') d\tau = \int_V \frac {1}{r^2 sinθ}\delta_r(r-r_0) \delta_θ (θ-θ_0) \delta_Φ (Φ-Φ_0) r^2...
  42. redtree

    I Understanding the Dirac Delta function

    I just want to make sure that I am understanding the Dirac Delta function properly. Is the following correct?: For two variables ##x## and ##y##: \begin{equation} \begin{split} \delta(x-y) f(x) &= f(y) \end{split} \end{equation} And: \begin{equation} \begin{split} \delta(x-x) f(x) &=...
  43. J

    2D Integrating With Quadratic Arg. of Delta Function

    Homework Statement I have a 2D integral that contains a delta function: ##\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\exp{-((x_2-x_1)^2)+(a x_2^2+b x_1^2-c x_2+d x_1+e))}\delta(p x_1^2-q x_2^2) dx_1 dx_2##, where ##x_1## and ##x_2## are variables, and a,b,c,d,e,p and q are some real...
  44. binbagsss

    Cts approximation, delta function integration, stat mech

    Homework Statement Homework EquationsThe Attempt at a Solution So cts approx holds because ##\frac{E}{\bar{h}\omega}>>1## So ##\sum\limits^{\infty}_{n=0}\delta(E-(n+1/2)\bar{h} \omega) \approx \int\limits^{\infty}_{0} dx \delta(E-(x+1/2)\bar{h}\omega) ## Now if I do a substitution...
  45. R

    Questions about the delta function

    Homework Statement I just have a quick question about the delta function, I'm pretty confident in most other cases but in this simple one I'm not so sure. $$\int_{-\infty}^{\infty} \phi (x)\delta (-x)dx$$ Homework EquationsThe Attempt at a Solution [/B] $$\int_{-\infty}^{\infty} \phi...
  46. cg78ithaca

    A Inverse Laplace transform of F(s)=exp(-as) as delta(t-a)

    This is mostly a procedural question regarding how to evaluate a Bromwich integral in a case that should be simple. I'm looking at determining the inverse Laplace transform of a simple exponential F(s)=exp(-as), a>0. It is known that in this case f(t) = delta(t-a). Using the Bromwich formula...
  47. Dopplershift

    Solving 3-D Dirac Delta Function Homework Question?

    Homework Statement \begin{equation} \int_V (r^2 - \vec{2r} \cdot \vec{r}') \ \delta^3(\vec{r} - \vec{r}') d\tau \end{equation} where: \begin{equation} \vec{r}' = 3\hat{x} + 2\hat{y} + \hat{z} \end{equation} Where d $\tau$ is the volume element, and V is a solid sphere with radius 4, centered...
  48. J

    I Square root of the delta function

    Is square root of delta function a delta function again? $$\int_{-\infty}^\infty f(x) \sqrt{\delta(x-a)} dx$$ How is this integral evaluated?
  49. C

    I How Does the Delta Function Impact Integral Calculations in Physics?

    I've come across the equation $$\int_0^1 dx \frac{dA(x)}{dx} + B = C = \text{finite}$$ in my readings on a certain topic in physics and, in both articles i have read, the following step is taken $$\int_0^1 dx \left( \frac{dA(x)}{dx} + (B-C)\delta(1-x) \right) = \text{finite}$$ For the...
  50. J

    I Evaluating 2D Delta Function Integral - Any Help Appreciated

    I am quite new here, and was wondering if anybody knows how this 2D integral is evaluated. $$ \int_{-\infty}^\infty \int_{-\infty}^\infty \delta(k_1 x-k_2y)\,dx\,dy$$Any help is greatly appreciated! Thanks!
Back
Top