Escape velocity Definition and 220 Threads
-

Velocity required to escape the solar system
For the (a) portion of the problem, it asks to calculate the minimum speed a probe must be launched from earth to escape the solar system with residual speed of 10 ##mi \, s^{-1}## relative to the sun. To find the minimum speed, I assumed the gravitational force affecting the probe by the sun...- theblazierbroom
- Thread
- Conservation of energy Escape velocity Orbital mechanics Orbital speed
- Replies: 15
- Forum: Introductory Physics Homework Help
-

I Finding Escape Velocity of mass (m) with electrostatic and gravitational influences
- PhysicsEnjoyer31415
- Thread
- Electrostatic potential Escape velocity Gravitation potential energy
- Replies: 17
- Forum: Classical Physics
-

Escape Velocity from Earth starting from its Centre
What is the minimum velocity (theoretically) of an object located at the CENTER of the Earth to move it outside its gravitational field?- Priyo137
- Thread
- Escape velocity Graviity Gravitation potential energy
- Replies: 27
- Forum: Introductory Physics Homework Help
-

I Balloon experiment - Classical Physics vs. Statistical Physics
While reading a similar and deservedly closed post a contradiction came to my mind. The supposed contradiction is related to Statistical Physics where my understanding is only conceptual so correct me where I might be wrong. I remember reading that lightweight gasses can escape Earth's...- Juanda
- Thread
- Classical physics Escape velocity Statisical mechanics
- Replies: 16
- Forum: Classical Physics
-

Escape velocity question - constant is wrong....
This is a multiple choice question. I assumed that this is an escape velocity question. I have been going round and round... Here's what I have done:- maxelcat
- Thread
- Constant Escape Escape velocity Velocity
- Replies: 4
- Forum: Introductory Physics Homework Help
-

Rocket Escape Velocity from the Earth-Sun system
I have a difficulty when making the energy-conservation-equation for the second step. When making the equation, we need to know the exact position (measured from the sun) of the rocket after it is freed from the Earth gravitation. But, where exactly does the rocket free from Earth...- Rikudo
- Thread
- Escape Escape velocity Rocket System Velocity
- Replies: 3
- Forum: Introductory Physics Homework Help
-
P
Escape velocity of solar system
I'm pretty confused by this but I have a few thoughts. Since the sun takes up most of the mass of the solar system, I was thinking maybe I'm really looking for the escape velocity of the sun? So I would use the mass of the sun for M and the radius of the sun for r. My other thought was to add up...- purpleperson1717
- Thread
- Escape Escape velocity Solar Solar system System Velocity
- Replies: 11
- Forum: Introductory Physics Homework Help
-
P
Calculate Earth's escape velocity using different methods
- Physicsdudee
- Thread
- Escape Escape velocity Velocity
- Replies: 8
- Forum: Advanced Physics Homework Help
-

Fields (Gravitational fields) -- Escape Velocity from the Moon
It's an MCQ, and I chose 4/81 v(esc). Is this correct? There isn't a marking scheme... :cry:- jellybean-spider
- Thread
- Escape Escape velocity Fields Moon Velocity
- Replies: 5
- Forum: Introductory Physics Homework Help
-
J
I Does Escape Velocity depend on a rocket's direction away from Earth?
He explain escape velocity in example where rocket goes straight up,isnt escacpe velocity ,velocity where centrifugal forces and gravity are equal,so refers only when rocket going in circle/orbit? Can rocket really leave Earth in straight line like he show in video once reach this velocity and...- Jurgen M
- Thread
- Direction Earth Escape Escape velocity Velocity
- Replies: 27
- Forum: Classical Physics
-
J
Escape Velocity Question: Why is the final kinetic energy = 0?
So Ekf-Eki+Epf-Epi=0. I understand that the final potential energy is 0 (distance away approaches infinity), but don't get why the final kinetic energy becomes 0. If the final kinetic energy was 0, wouldn't that mean the object no longer has any velocity and would start being effected by the... -

I Derive Escape Velocity GR: Source for Schwarzschild Metric
I was surprised to read that the formula for escape velocity — at least for a spherical mass like the Earth — is the same in relativity as it is in classical physics: v_e = (2GM/r)^{1/2} I'm wondering if someone can give me a good source for deriving this. (I assume one takes a radial...- snoopies622
- Thread
- deriving Escape Escape velocity Gr Velocity
- Replies: 7
- Forum: Special and General Relativity
-

Finding r of a Jovian-synchronous orbit and escape velocity
1. The satellite would be in a jovian-synchronous orbit, Rearranging the formula for the orbital period in terms of r, since T^2 is proportional to r^3: T^2=4π^2r^3/GM which becomes r^3=(GM/4π^2) T^2 M(mass of Jupiter)=1.89 x 10^27 G=6.67*10^-11 m^3kg^-1s^-2 T=9 hours and 55 minutes =...- AN630078
- Thread
- Escape Escape velocity Orbit Velocity
- Replies: 7
- Forum: Introductory Physics Homework Help
-

A mistake in the derivation of escape velocity
In the last step of the derivation of escape velocity, the two sides of the equation seem to have opposite signs. $$-1/2mv_0^2=-mgR_e^2\,\lim_{r\to\infty}(1/r-1/R_e)$$ $$-1/2mv_0^2=mgR_e^2 \frac{1}{R_e}$$ Since the mass and the square of the velocity are positive, the left side of the equation...- Leo Liu
- Thread
- Derivation Escape Escape velocity Mistake Velocity
- Replies: 5
- Forum: Introductory Physics Homework Help
-
I
What is the geometrical connection between escape velocity and orbital velocity?
If you derive the equation for orbital velocity you get \begin{equation} v_{orbit} = \sqrt{\frac{GM}{R}} \end{equation} and for escape velocity you get \begin{equation} v_{escape} = \sqrt{\frac{2GM}{R}}=\sqrt{2}\,v_{orbit} \end{equation} I'm wondering if there is a logical/geometrical... -

Escape Velocity depends on the Radius of the Earth?
We have 2 different formulas for escape velocity. and . If we look at the first formula we see that escape velocity is inversely proportional to the square root of Radius of Earth. While in the second formula, escape velocity is directly proportional to the square root of Radius of Earth. We...- Muhammad Danish
- Thread
- Earth Escape Escape velocity Radius Velocity
- Replies: 13
- Forum: Mechanics
-

Find the escape velocity from 2 point charges
Below is the work I've attempted. I used 2 PE b'c there were 2 point charges, and only one KE b'c only the proton is moving. The final equation in case it's hard to see is V(esc) = sqrt (4kQq / mr). I'm not sure if I did it right. Did I set up this equation right? and I am also not sure what...- r-swald
- Thread
- Charges Escape Escape velocity Point Point charges Velocity
- Replies: 4
- Forum: Introductory Physics Homework Help
-
J
What is the kinetic energy when an object reaches escape velocity?
What is the kinetic energy equal to during the escape velocity? Henceforth, what is exactly happening at the escape velocity in terms of gravity?- Josielle Abdilla
- Thread
- Energy Escape Escape velocity Kinetic Kinetic energy Velocity
- Replies: 5
- Forum: Mechanics
-

Escape velocity and gravitational freefall
Is an object with escape velocity in gravitational freefall? -
B
Calculating Escape Velocity for Earth: Where Am I Going Wrong?
I really cannot understand where this is going wrong... Plugging in the constants, I get vescape=Sqrt(2(6.67x10^-11)(5.976x10^24kg)/6378). (6.67x10^-11)(5.976x10^24kg) gives me 3.99x10^14, and multiplied by 2 gives me 7.97x10^14. 7.97x10^14/6378=1.25x10^11. The square root of 1.25x10^11 would...- breid040
- Thread
- Escape Escape velocity Velocity
- Replies: 2
- Forum: Introductory Physics Homework Help
-
G
I Escape Velocity, Gravitational Velocity & Time Dilation
The is a question about gravitational time dilation and escape velocity. As others have pointed out, you may use escape velocity to calculate gravitational time dilation in a gravitational field. (Interestingly, you can't use gravity to calculate gravitational time dilation, which makes...- Grav Velocity
- Thread
- Dilation Escape Escape velocity Gravitational Time Time dilation Velocity
- Replies: 37
- Forum: Special and General Relativity
-
A
Escape velocity of an iron asteroid
Homework Statement: Jack can jump upwards a distance 1.4 meters when he is on the surface of the Earth. What is his initial velocity when he jumps? Most of the time, however, Jack is in space. He is an asteroid miner: he looks for asteroids made out of useful metals. His job involves landing on...- ac7597
- Thread
- Asteroid Escape Escape velocity Gravity Iron Velocity
- Replies: 5
- Forum: Introductory Physics Homework Help
-
D
Unusual escape velocity derivation
Is it possible to derive escape velocity say using momentum and force balance considerations? or using angular momentum consideration? Namely, any other approach then energy consideration that utilizes gravitation potential energy and kinetic energy? -
Z
When would a rocket return that was at escape velocity
we all know escape velocity is a velocity in which a body can escape orbit around the Earth and fly off into space. this needs to happen in space our just out of our atmosphere, due to drag that could bring an object back into orbit and cause it's velocity to degrade to a point where it would... -
L
Question About the Escape Velocity from Different Mass Planets
Hi! I have a question about escape velocity. If a planet is bigger and have a greater escape velocity than another planet. Do this effect the density of the bigger planet in any way? Or do we have to know the mass of the bigger planet to know if the density is larger or lower for this planet? -
S
I Escape Velocity: Newtonian vs Relativistic
Hi, Do we obtain the same escape velocity equation: Ve = sqrt(2GM/r) using both Newtonian and Relativistic approach?- sha1000
- Thread
- Escape Escape velocity General General relaivity General relativity Relaitivity Relativity Special relativity Velocity
- Replies: 18
- Forum: Special and General Relativity
-
C
Escape Velocity and the Motion of Two Massive Bodies
Hey there, If body 1, mass M1 has escape velocity V_e1 = (2GM1/r)**.5 but M2 is more massive than M1 is this relation still valid? In this case, the subordinate body really isn't the subordinate body so does this still hold? And r (distance b/t the two) changes not only due to the motion of M2...- Conor Smith
- Thread
- Classical mechanics Confusion Escape Escape velocity Gravity Velocity
- Replies: 4
- Forum: Mechanics
-

Escape velocity when the rocket's mass is not small compared to the asteroid
Hello When one calculates the speed of liberation of an object with respect to a star, one takes into account the force exerted by the star on the object. But not the force exerted by the object on the star. For small objects, this is valid. But what is the speed of release of a 1000 kg rocket... -
H
Find the speed of a satellite at a distance R from Earth
Homework Statement Gravitational force exerted on mass m is GMm/r^2 2. Relevant equations Orbital velocity at distance R from Earth = ##\sqrt gR## Escape velocity = ##\sqrt 2gR## gR = GM/R Fc = mV^2/R F =m.aThe Attempt at a Solution 1) express acceleration of gravity in terms of G, M , and R...- Helly123
- Thread
- Earth Escape velocity Orbital angular momentum Orbital velocity Satellite Speed
- Replies: 39
- Forum: Introductory Physics Homework Help
-
W
Escape Velocity and Centripetal/Centrifugal Acceleration
This is just a reality that I have stumbled upon that I'm sure was well-known, but I still found it interesting. I apologize if this is second-nature to physics experts. I was responding to a post on a different thread that claimed you could make a tunnel around the Earth and if you sent a...- willoughby
- Thread
- Acceleration Escape Escape velocity Velocity
- Replies: 7
- Forum: Mechanics
-

I How does the speed of light affect expansion acceleration?
I may have a fundamental misunderstanding of the concept, but I was wondering, how does the accelerating expansion of the universe calculate for the time dilation in light travel? From my understanding, we know that the universe expansion is accelerating because the farthest galaxies that we...- Joe Fatuch
- Thread
- Acceleration Escape velocity Expansion Hubble Light Red shift Speed Speed of light
- Replies: 15
- Forum: Cosmology
-

Escape velocity and kinetic energy of the Earth
If you had two masses, m_{1} and m_{2}, and you released them in space infinitely far apart, their kinetic energies would satisfy \frac{1}{2}m_{1}v_{1}^2+\frac{1}{2}m_{2}v_{2}^2=\frac{Gm_{1}m_{2}}{r} if they met with a distance r between their centres of mass. This equation therefore tells you...- Alexander350
- Thread
- Earth Energy Escape Escape velocity Gravity Kinetic Kinetic energy Mechanics Velocity
- Replies: 6
- Forum: Mechanics
-
R
Intuition for why escape velocity doesn't depend on angle
Homework Statement solve for escape velocity from Earth's surface Homework Equations just either use the line integral, and the tangential term disappears, or just use the energy equations The Attempt at a Solution I've solved it, but I'm having some trouble just coming to grips with this...- RubinLicht
- Thread
- Angle Escape Escape velocity Intuition Velocity
- Replies: 9
- Forum: Introductory Physics Homework Help
-
A
I Can a plane escape Earth's gravity with a powerful engine and no air?
If I drive a plane and the force of engine is bigger than force of gravity of it , if the engine is turn on always ,and assuming no air , will the plane continue moving up and escape from the gravity ?- ahmed emad
- Thread
- Escape Escape velocity Forces Gravity
- Replies: 8
- Forum: Classical Physics
-
A
GPE and Escape Velocity: Understanding the Relationship for Moving Objects
Is it necessary to be the kinetic energy greater than gpe to move ( I don't talk about in orbits) Example : Is it will be harder to move an object has a bigger gpe ( same mass but bigger hight from ground). And thanks.- ahmed emad
- Thread
- Escape Escape velocity Gpe Gravitational potential energy Kinetic energy Velocity
- Replies: 20
- Forum: Mechanics
-
G
KE+PE when a rocket's speed is less than escape velocity?
Hey people, I just want to ask that what will happen to the total mechanical force of the rocket if its speed is less than escape velocity? a. KE+PE=0 b. KE+PE>0 c. KE+PE<0 d. Depends upon initial speed of the rocket Pick one. And Why??- GrimReaper
- Thread
- Escape Escape velocity Speed Velocity
- Replies: 8
- Forum: Introductory Physics Homework Help
-
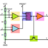
Pytels Dynamics 12.8: Missile dynamics, acceleration and escape velocity
Homework Statement A missile is launched from the surface of a planet with the speed v0 at t=0. According to the theory of universal gravitation, the speed v of the missile after launch is given by v2 = 2gr0(r0 / r -1) + v02 where g is the gravitational...- Alexanddros81
- Thread
- Acceleration Dynamics Dynamics kinematics Escape Escape velocity Missile Velocity
- Replies: 6
- Forum: Introductory Physics Homework Help
-
D
B Escape Velocity from Relativistic Sphere: Derivation & Intuition
Can you please direct me to ref that shows the derivation of the escape velocity from a spherical object that moves in velocity v~c with respect to rest frame? I suspect the escape velocity is increasing (intuitively since the mass increases). Please comment and suggest alternatives.- Dilema
- Thread
- Escape Escape velocity Relativistic Sphere Velocity
- Replies: 2
- Forum: Special and General Relativity
-

B An exercise related to the mass of the Milky Way, sort of.
So, in preparation to the Portuguese Astronomy Olympiads, I've stumbled upon this problem (exercise): The sun, which is 8 kpc away from the centre of the Milky Way, has a rotation speed of approximately 220 kms-1 . Whereas a a star that is 15 kpc from the centre of the Galaxy orbits at a speed...- TreeLover
- Thread
- Escape velocity Exercise Kepler's third law Mass Milky way Sort
- Replies: 2
- Forum: Astronomy and Astrophysics
-

Need help finding energy for escape velocity
Homework Statement The gravitational potential energy of a certain rocket at the surface of the Earth is -1.9x10^12 J. The gravitational potential energy of the same rocket 300km above the Earth's surface is -1.8x10^12 J. Assume the mass of the rocket is constant for this problem. A) How much...- Jared
- Thread
- Energy Escape Escape velocity Kinetic energy Orbital Rocket Velocity
- Replies: 5
- Forum: Introductory Physics Homework Help
-

Trip to Space -- Can ship with 1g acceleration escape Earth?
In another forum, the question was raised, "could a ship with 1G acceleration escape the gravity well of a planet with 1G gravity?" A popular response is, if the craft is aerodynamic, it could accelerate laterally until it reached escape velocity and then manage to get to space. I don't... -
J
Need help calculating acceleration out of a gravity well
Hey, orbital mechanics! I can't find what I need to figure this out on the internet, and I don't do calculus so I don't understand all that I find. Help me make my next sci-fi novel plausible? I just did an Oberth maneuver around Sol, 21 radii (.0977 AU, 14,616,000 km) from center... -
D
Is the usual Escape Velocity eqn an approximation?
Text books ordinarily give the escape velocity of a mass-M body (in the center of mass frame of the system of the body and the escaping projectile, whose mass I'll label m) as (*) v2 = 2GM/r where r is the distance between the body and the escaping projectile. it doesn’t seem to me that (*)...- David Baker
- Thread
- Approximation Escape Escape velocity Velocity
- Replies: 2
- Forum: Mechanics
-

How come escape velocity isn't imaginary?
Going through several definitions, it appears that escape velocity is equal to the potential energy. That is:$$\frac{1}{2}m v^2=-\frac{G M m}{r}$$but if I solve for velocity, $v$, I get:$$v=\sqrt{-2\frac{G M}{r}}$$So how do I get an escape velocity that isn't imaginary?- Jules Winnfield
- Thread
- Escape Escape velocity Gravity Imaginary Potential energy Velocity
- Replies: 4
- Forum: Mechanics
-

Escape Velocity of a Neutron Star: Relativistic Calculation
Homework Statement Calculate the escape velocity on the surface of the neutron star in the previous problem (##m = \frac{2}{3} \cdot 2,1 \cdot M_{\odot}##; ##R = 15km##). Hint: Basic physics. Note, however, that the escape velocity is not going to be small when compared to the speed of light...- TheSodesa
- Thread
- Conservation of energy Escape Escape velocity Relativistic Relativistic energy Special relativity Velocity
- Replies: 1
- Forum: Introductory Physics Homework Help
-
S
Rocket Launch: Achieving Escape Velocity w/ Fuel-Mass Ratio of 300
Homework Statement Rockets are propelled by the momentum of the exhaust gases expelled from the tail. Since these gases arise from the reaction of the fuels carried in the rocket, the mass of the rocket is not constant, but decreases as the fuel is expended. Show that for a Rocket starting...- Sudo
- Thread
- Analytical mechanics Classical mechanics Escape Escape velocity Launch Mechanics Physics Ratio Rocket Rocket science Velocity
- Replies: 3
- Forum: Introductory Physics Homework Help
-

B What does a black hole look like from the inside?
According to this video, , if a black hole is large enough you could actually travel for some time within the event horizon without dying because the event horizon is so far from the actual singularity. So, assuming that's true, what would you see while you were inside the black hole? Here's...- GiantSheeps
- Thread
- Black hole Escape velocity Event horizon Hole Light Speed of light
- Replies: 4
- Forum: Astronomy and Astrophysics
-
R
Escape Velocity: Unraveling the Mysteries of Kinetic & Potential Energy
Why does a planet's kinetic energy become 0 when it reaches infinity? And why does a planet's kinetic energy get converted to gravitational potential energy when subjected under another planet's gravitational field? Escape velocity seems very abstract to me!- Rachana MN
- Thread
- Escape Escape velocity Physics Velocity
- Replies: 1
- Forum: Astronomy and Astrophysics
-
L
B Escape Velocity & Black Holes: Can Something Escape?
It is my understanding of black holes that nothing can escape them because their escape velocity is higher than the speed of light. The place at which the escape velocity becomes higher than the speed of light is known as the event horizon. My question is what happens if there is a normal force...- livethere
- Thread
- Black holes Escape Escape velocity Holes Velocity
- Replies: 3
- Forum: Special and General Relativity
-

D.E. Littlewood's comments about escape velocity
I have been reading D.E. Littlewood's book "The Skeleton Key of Mathematics", and near the beginning he says that if a projectile weighing one (long) ton were given a velocity of 44 miles a second, this would be "sufficient to raise it to a height of 1000 miles above the Earth's surface."...