Geometric Definition and 790 Threads
-
S
Calculating Vertical Distance & Tree Age | Geometric Question Solution
Homework Statement 1)A hard rubber ball is dropped from a moving truck with a height of 5 m. The ball rises of the height from which it fell after each bounce. the total vertical distance the ball has traveled at the moment it hits the ground for the eighth time, to the nearest tenth of a...- Suy
- Thread
- Geometric
- Replies: 8
- Forum: Precalculus Mathematics Homework Help
-
B
Special Relativity - geometric approach?
Hi everybody: does anyone know of a good book on special relativity that takes a geometric approach? I'm doing research that requires that I know special relativity, and, while working problems out for personal-practice, all I do is either: 1) make gamma-messes 2) clumsily-use invariants...- bjnartowt
- Thread
- Approach Geometric Relativity Special relativity
- Replies: 2
- Forum: Science and Math Textbooks
-
S
HELP geometric probability: area of a square and conditional probability
Homework Statement Chose a point at random in a square with sides 0<x<1 and 0<y<1. Let X be the x coordinate and Y be the y coordinate of the point chosen. Find the conditional probability P(y<1/2 / y>x). Homework Equations No clue. The Attempt at a Solution Apparently, according...- SusanCher89
- Thread
- Area Conditional Conditional probability Geometric Probability Square
- Replies: 4
- Forum: Precalculus Mathematics Homework Help
-
T
Distribution to geometric standard deviation
Hi, can someone just confirm that to get the GSD of a distribution, I simply take the natural log (or log 10?) of all the numbers then find the arithmetic standard deviation of that? Thanks :)- thomas49th
- Thread
- deviation Distribution Geometric Standard Standard deviation
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
S
Calculating pH in Geometric Units: Solving a Tricky Acidic Battery Question
Homework Statement If the ph of battery acid should be 0.8, what is the pH of the acid in a battery that is one-fifth as acidic as it should be? Homework Equations The Attempt at a Solution We just learned how to comparing pH in Geometric unit, using the formula 10^(ph1-ph2). But...- Suy
- Thread
- Geometric
- Replies: 7
- Forum: Precalculus Mathematics Homework Help
-

Equivalent resistance/ geometric resistor network
Homework Statement hi guys, i'm having trouble applying Kirchhoff's laws to determine the equivalent resistance of this symmetrical array of resistors (see attachment); i think there is a quick trick, using 4 current loops, but i can't remember it... nor find relevant documentation – this is...- Goddar
- Thread
- Equivalent Equivalent resistance Geometric Network Resistance Resistor
- Replies: 7
- Forum: Introductory Physics Homework Help
-
F
Eigenvalue - geometric multiplicity proof
Homework Statement Given matrix A: a 1 1 ... 1 1 a 1 ... 1 1 1 a ... 1 .. . .. ... 1 1 1 1 ... a Show there is an eigenvalue of A whose geometric multiplicity is n-1. Express its value in terms of a. Homework Equations general eigenvalue/vector equations The Attempt at a Solution My...- flashdrive
- Thread
- Eigenvalue Geometric multiplicity Proof
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
O
Organic Chemistry Geometric Isomers Lab
Homework Statement The experiment was changing dimethyl maleate into dimethyl fumerate, with the intent of being analogous to changing maleic acid into fumeric acid. In the experiment, we added 1 M Bromine in dimethylchlorine to our dimethyl fumerate, put the mixture in a hot water bath and...- ohgeecsea
- Thread
- Chemistry Geometric Isomers Lab Organic Organic chemistry
- Replies: 1
- Forum: Biology and Chemistry Homework Help
-
S
Electric Potential energy for geometric objects
I recently found out how to calculate the potential energy of a charged insulated sphere of radius R and charge density rho. I would like to know how to calculate the potential energy for other geometric objects, such as a line of charges, a sheet of charges, or a pyramid of charges. I don't...- simpleton
- Thread
- Electric Electric potential Electric potential energy Energy Geometric Potential Potential energy
- Replies: 13
- Forum: Electromagnetism
-
C
Geometric Progression Question
Hi. Tried solving, but no idea how. At the end of 1995, the population of Ubris was 46650 and by the end of 2000 it had risen to 54200. On the assumption that the population at the end of each year form a g.p. find a) The population at the end of 2006, leaving your answer in 3 s.f. b)...- crays
- Thread
- Geometric
- Replies: 6
- Forum: Precalculus Mathematics Homework Help
-
D
Probability - Geometric Random Variable
Homework Statement Let X be a random variable with distribution function px(x) defined by: px(0) = a and px(x) = Px(-x) = ((1-a)/2)*p*(1-p)^(x-1), x = 1,2... where a and p are two constants between 0 and 1, and px(0) is meant to be the probability that X=0 a) What is the mean of X...- Dark Wanderer
- Thread
- Geometric Probability Random Random variable Variable
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
N
Geometric Sequences: Solving Homework Questions
Homework Statement Hi, there are two questions that I'm quite stuck with. 1.Find the number of terms in each of these geometric sequences. a) 1,-2,4...1024 b) 54,18,6...2/27 Homework Equations ar^n-1 The Attempt at a Solution 1. a) r= -2 1x-2^n-1 ? b)...- nomad2817
- Thread
- Geometric Sequences
- Replies: 6
- Forum: Precalculus Mathematics Homework Help
-
N
Solve for nGeometric Sequences: Solving for Number of Terms
Homework Statement Hi, I was trying to work out this question, but i kinda got stuck. Can anyone help me please? Thanks 4. Find the number of terms in each of these geometric sequences. 2,10,50...1250 Homework Equations ar^n-1 The Attempt at a Solution 1250=2x5^n-1- nomad2817
- Thread
- Geometric Sequences
- Replies: 20
- Forum: Precalculus Mathematics Homework Help
-
J
A matrix is diagonalizable when algebraic and geometric multiplicities are equal
A matrix is diagonalizable when algebraic and geometric multiplicities are equal. My professor proved this in class today, but I did not fully understand his explanation and proof. Can someone please help?- jack_bauer
- Thread
- Geometric Matrix
- Replies: 2
- Forum: Linear and Abstract Algebra
-
J
A matrix is diagonalizable when algebraic and geometric multiplicities are equal
A matrix is diagonalizable when algebraic and geometric multiplicities are equal. I know this is true, and my professor proved it, but I did not understand him fully. Can someone please explain?- jack_bauer
- Thread
- Geometric Matrix
- Replies: 2
- Forum: Linear and Abstract Algebra
-
S
Geometric Optics- Refraction , reflected ray's
Homework Statement A beam of light in air makes an incident angle with the normal at 53 with an unknown substance. Part of the light is relected and part is refracted into the substance. The reflected ray and the refracted ray make an angle of 90 degrees. a) What is the refracted angle...- sally143
- Thread
- Geometric Geometric optics Optics Refraction
- Replies: 9
- Forum: Advanced Physics Homework Help
-
L
Question on finite and geometric series
1. 1. Find the exact(no approximations)sum for the finite series S sub n= (2 + 2 + 2(2+...+64 i used the parentheses to represent a radical sign 2. Show that the sum of the first 10 terms of the geometric series 1 + 1/3 + 1/9 + 1/27+... is twice the sum of the first 10 terms of...- Luceian K
- Thread
- Finite Geometric Geometric series Series
- Replies: 12
- Forum: Precalculus Mathematics Homework Help
-

Geometric Progression: Ball Bouncing Distance Calculation | Homework Solution
Homework Statement A ball is dropped vertically from height h onto a flat surface, after the nth bounce it returns to high h / 3^n. Find the total distance traveled by the ball. Homework Equations Sum (infinity) = \frac{a}{1 - r} The Attempt at a Solution I don't see the...- Chewy0087
- Thread
- Geometric
- Replies: 2
- Forum: Precalculus Mathematics Homework Help
-
J
Geometric intepretation of matrices
Is there a geometric interpretation of any n*n matrix?- JG89
- Thread
- Geometric Matrices
- Replies: 9
- Forum: Linear and Abstract Algebra
-
R
Partial sum of geometric series
ok so i know how to calculate the partial sum of a geometric series. But let's say i only want to calculate the sum of every other term, how would i do this? example: .5^0+.5^1+.5^2+...+.5^n = (.5^(n+1) - 1)/(.5-1) but what equation can i use to get the sum of only these terms...- realitybugll
- Thread
- Geometric Geometric series Partial Series Sum
- Replies: 3
- Forum: General Math
-
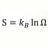
Geometric area integration of 1/x
given: ln (x) = integral 1/t dt from 1 to x and x=30 Without a calculator and only a graph of y=1/x How could you show that this geometric area under this curve (with any type of unit) is equal to 3.4 area units, the ln (30) not homework, I am looking for a tangible/physical... -
I
Proving the Integer Rectangle Property: A Geometric Puzzle
Not homework but this is probably the best suited place for a puzzle: A large rectangle in the plane is partitioned into smaller rectangles, each of which has either integer height or integer width (or both). Prove that the large rectangle also has this property. I've given this several...- intrepid_nerd
- Thread
- Geometric Puzzle
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
S
Geometric Proofs: Is the Point Obvious?
Is there a point to geometric proofs? The ones that I have encountered are so obvious that it almost seems useless to have to use them for anything.- Stratosphere
- Thread
- Geometric Point Proofs
- Replies: 2
- Forum: General Math
-
S
Geometric representation of composite numbers
Some years ago I used the device of representing composite numbers by rectangular forms to demonstrate the structure of numbers to third grade students. Primes were represented by lines of various lengths. Number 10 would be a 2x5 rectangle and 20 a 2x2x5 rectangular solid. (I used various...- SW VandeCarr
- Thread
- Composite Geometric Numbers Representation
- Replies: 17
- Forum: Linear and Abstract Algebra
-
B
Understanding Abstract Algebra: A Geometric Approach
I'm taking a class in abstract algebra this summer, so I thought I'd get ahead by reading the book before class starts. This is from a book called "Abstract Algebra: A Geometric Approach", chapter 1: Applying the Principle of Mathematical Induction with a slight modification. If S' \subset \{n...- Bill Foster
- Thread
- Abstract Abstract algebra Algebra Approach Geometric
- Replies: 1
- Forum: Linear and Abstract Algebra
-
J
Geometric Series and Triple Integrals
Homework Statement \int 1/(1-xyz)dxdydz = \sum1/n3 from n = 1 to infiniti dx 0 to 1 dy 0 to 1 dz 0 to 1 Homework Equations The Attempt at a Solution Not sure how to relate the two of them- joemama69
- Thread
- Geometric Geometric series Integrals Series Triple integrals
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
R
Geometric Sequence and Recursive Definition
Homework Statement In a Geometric Sequence find t10. t3 = 4 and t6= 4/27 Give a recursive definition for the sequence: 1, 4, 13, 40... Homework Equations I know that a Geometric sequence is: tn=t1(r)n-1 And that a recursive formula starts off with tn-1 I'm not sure where to go...- rought
- Thread
- Definition Geometric Sequence
- Replies: 1
- Forum: Precalculus Mathematics Homework Help
-
H
Proving Proportionality of Areas with Affine Geometry
Homework Statement Show that the ratio of areas is proportional to the sides squared: \frac{[ACD]}_{[CDB]} is proportional to \frac{AC^2}_{CB^2} Please, see the picture: http://dl.getdropbox.com/u/175564/geo_henry.JPG . Homework Equations AC = 2 * CB \frac{AD}_{DB} is propotional to...- Horse
- Thread
- Geometric
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
R
Understanding Geometric Distribution
Geometric Distribution? Geometric Distribution: In an experiment, a die is rolled repeatedly until all six faces have finally shown.? What is the probability that it only takes six rolls for this event to occur? ANSWER = 0.0007716 What is the expected waiting time for this event to occur...- rclakmal
- Thread
- Distribution Geometric Geometric distribution
- Replies: 5
- Forum: Precalculus Mathematics Homework Help
-

Geometric intepretation of Taylor series
Sorry, the title should be: geometric intepretation of moments My question is: does the formula of the moments have a geometrical interpreation? It is defined as: m(p) = \int{x^{p}f(x)dx} If you can't see the formula it is here too: http://en.wikipedia.org/wiki/Moment_(mathematics) with c=0... -
S
Clarifying Geometric and Material Buckling
Hello everyone, I am studying for an upcoming exam and have become somewhat confused as to exactly what geometric and material buckling represent. Are they representative of the shape of the neutron flux distribution in the reactor? Are these quantities related to the structural deformation...- Szymanski
- Thread
- Buckling Geometric Material
- Replies: 2
- Forum: Nuclear Engineering
-
M
Prove a Cauchy Sequence using Geometric Sums
Homework Statement Let {x_n} be a sequence. and let r be a real number 0<r<1. Suppose |x_(n+1) - x_n|<=r|x_n -x_(n-1)| for all n>1. Prove that {x_n} is Cauchy and hence convergent. Homework Equations if |r|<1 then the sequence \sum r^k from k=0 to n converges to 1/(1-r) The...- mathkiddi
- Thread
- Cauchy Geometric Sequence Sums
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
B
Determine the Geometric generating function
Homework Statement Suppose RX(t) = E[(1 − tX)−1] is called the geometric generating function of X. Suppose the random variable Y has a uniform distribution on (0, 1); ie fY (y) = 1 for 0 < y < 1. Determine the geometric generating function of Y . Homework Equations The Attempt at...- boneill3
- Thread
- Function Geometric
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

Complex Vectors in Geometric Algebra
Hello, I have recently started to study some Geometric Algebra. I was wondering how should I interpret complex-vectors in \mathcal{C}^n in the framework of Geometric Algebra. I understand already that a complex-scalar should be interpreted as an entity of the kind: z = x + y (\textbf{e}_1...- mnb96
- Thread
- Algebra Complex Complex vectors Geometric Geometric algebra Vectors
- Replies: 5
- Forum: Linear and Abstract Algebra
-
L
Geometric Progression: Calculating the nth Partial Sum
what is the nth partial sum of 1-x+x^2-x^3+.. i don't understand why i can't do this? i have \sum_{k=1}^{n} ar^k=\frac{a(r^{n+1}-r)}{r-1} ok but then when i sub in i get messed up i get \frac{(-x)^{n+1}+x}{-(1+x)} is there any way of simplifying this? also when i set n=1 i get that...- latentcorpse
- Thread
- Geometric
- Replies: 8
- Forum: Precalculus Mathematics Homework Help
-
S
Geometric Series - Finding a Partial Sum Equation
Is it possible to find the partial sum equation for (2^m - 1)/3^m, from m=0 to m=n-1? I know that I'm supposed to rearrange the expression into the format ar^m, so the exponent m must only be on the value r, and not on the constant a. So far the farthest I've gotten is to rearrange it into...- Sean O
- Thread
- Geometric Geometric series Partial Series Sum
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
H
Geometric description homework
Homework Statement In each case give a geometric description of the cosets of H in G. a) G=R*, H=R+ b) G=C*, H=R Homework Equations The Attempt at a Solution I have no idea about geometric description...- hsong9
- Thread
- Geometric Homework
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
N
Geometric Series with probability
Using the formula for the sum of geometric series, show that the values of p(n) sum to 1 p(n)=(1 - \alpha)^n \alpha My attempt: \alpha \sum^\infty_{{\bf n=0}} (1- \alpha)^n I am not sure where to go from here. Any help to show this is true!- needhelp83
- Thread
- Geometric Geometric series Probability Series
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
L
What is the Inverse Matrix for A?
Homework Statement If A = [ -4e^4t sin(9t) -4e^5t cos (9t) ] [ 4e^4t cos (9t) -4te^5t sin (9t) ] then A^-1 = [ ___ ___ ] [ ___ ___ ] Homework Equations how do you deal with the exponents? The Attempt at a Solution Put into RREF, and then see what the inverse is?- LaraCroft
- Thread
- Geometric Matrix
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
F
Convergence and Sum of Geometric Series - Homework Question
Homework Statement actually got two questions but both are related so put them in the same place the question asks Determine whether the geometric series is convergent or divergent. If it is convergent, find its sum. Inf 1.) E 6(0.9)^(n-1) n=1 Inf (-3)^(n-1)...- fball558
- Thread
- Geometric Geometric series Series
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
E
Geometric algebra vs. differential forms
Recently I discovered geometric algebra which looks very exciting. I was wondering if there is any connection between geometric algebra and differential forms? I see that different research groups recommend the use of differential forms (http://www.ee.byu.edu/forms/forms-home.html" ), and...- element4
- Thread
- Algebra Differential Differential forms Forms Geometric Geometric algebra
- Replies: 2
- Forum: General Math
-
S
Geometric Optics: Snell's Law calculation problem
Homework Statement Calculate the angle of incidence for an angle of refraction of 10° for a) Diamond (2.42) to air θ2=Angle of refraction=10° n2=Index of refraction on refractive medium=1 n1=index of refraction on incident medium=2.42 θ1=? Homework Equations n1sinθ1=n2sinθ2...- StupidGenius
- Thread
- Calculation Geometric Geometric optics Law Optics Snell's law
- Replies: 4
- Forum: Introductory Physics Homework Help
-
6
Geometric Distribution and probability
Homework Statement Assume that each of your calls to a popular radio station has a probability of 0.02 of connecting, that is, of not obtaining a busy signal. Assume that your calls are independent. What is the probability that it requires more than five calls for you to connect...- 6021023
- Thread
- Distribution Geometric Geometric distribution Probability
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
H
Understanding Geometric Sequences with ln
Homework Statement http://img16.imageshack.us/img16/2327/nummer1.jpg Homework Equations Sn=(u1(rn-1))/(r-1) The Attempt at a Solution I think i need to use the equation for geometric series(above). Or do i use the arithmetic furmula since ln(a/b)=ln(a)-ln(b). I think i am a bit...- hostergaard
- Thread
- Geometric Ln
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
G
Studying Geometric Algebra: Degenerate & Nondegenerate Forms Explained
I'm trying to study geometric algebra using Artin's book and am having some difficulty with what degenerate symmetric bilinear forms would be like. Does someone know of an example and brief explanation. Also, the opposite being "nondegenerate nonsymmetric bilinear form" would help me out. If I...- Gott_ist_tot
- Thread
- Algebra Forms Geometric Geometric algebra
- Replies: 1
- Forum: Linear and Abstract Algebra
-
S
Vectors As Geometric Objects And Reciprocal Basis?
I'm trying to build up enough understanding to work through some GR on my own, but I'm horribly confused by some of the math concepts. So terribly so, that I'm not even sure how to ask my questions. Please bear with me. Lets work in a 2D plane. Assume I have a vector u which I can write out...- ShreddedWheat
- Thread
- Basis Geometric Reciprocal Vectors
- Replies: 6
- Forum: Differential Geometry
-
M
Defining Geometric Terms: Line, Point, "Lie On", Between, Congruent
Homework Statement Define the following terms: a) Midpoint M of segment AB. b) Perpendicular bisector of a segment AB (you may use the term "midpoint" since ypu have just defined it). c) Ray BDbisects angle ABC (given that point D is between A and C) d) Points A, B, and C are collinear...- mamma_mia66
- Thread
- Geometric Line Point Terms
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
N
Crude geometric estimation or am I missing something?
Homework Statement I'm doing a report for a physics lab experiment where we are calculating the radius of the Earth by measuring the time it takes to see the sunset from the base of a cliff looking out into the pacific ocean till when it sets in relation to an observer at the top of the...- neolayman
- Thread
- Estimation Geometric
- Replies: 3
- Forum: Precalculus Mathematics Homework Help
-
M
Organic Chemistry- Geometric and Structural Isomers of C6H12
Homework Statement Draw and name all of the structural isomers of hydrocarbons with the formula C6H12 (cyclohexane). 2. Relevant information This is "only" a grade 11 Chemistry Assignment, therefore I only really need the basics when it comes to isomers- not some of the more complex...- MarquisDM
- Thread
- Chemistry Geometric Isomers Organic Organic chemistry Structural
- Replies: 4
- Forum: Biology and Chemistry Homework Help
-
M
Geometric optics - why pinhole bends rays like lens
We were discussing in an https://www.physicsforums.com/showthread.php?t=284322" that pinholes work like lenses, in that they form inverted real images. The other day, a friend told me, that pinholes even do bend the light rays like a lens do. I can - as being nearsighted - actually use a pinhole...