Intersection Definition and 688 Threads
-
P
Detecting Intersections of Functions: Is There a Foolproof Method?
Does anyone know of an algorithm to detect the intersection of any two functions - both for individual points within a fixed range of x values and determining whether or not total points of intersection are finite or infinite over an infinite range of x values? Also, is this possible to do this... -
S
Points Nearest/Farthest from Origin on Plane-Paraboloid Intersection?
Homework Statement Find the points nearest and furthest from the origin on the intersection of a plane with a paraboloid. Plane: x+y+2z=30 Paraboloid: z=x^{2}+y^{2} Homework Equations The Attempt at a Solution Obviously the first step is to find the equation of the...- skyturnred
- Thread
- Intersection Origin Plane Points
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
U
Finding Intersection of Tangents on a Circle
Homework Statement Two points represented by z_{1}, z_{2} lie on circle |z|=1, the tangents to the circle at these points meet at the point represented by Homework Equations The Attempt at a Solution Let the tangents meet at the point z_{3}. The centre of the given circle is (0,0)...- utkarshakash
- Thread
- Intersection
- Replies: 11
- Forum: Precalculus Mathematics Homework Help
-
P
Finding intersection of line and circle.
Homework Statement I have a line obtained from using a slope of 1 and point (-sqrt(2),sqrt(2)): y - sqrt(2) = 1 (x+sqrt(2)) y = 2*sqrt(2) + x and a circle with radius 5 centered at origin. My thought was to solve this parametrically The line is the tangent line (blue...- ParoXsitiC
- Thread
- Circle Intersection Line
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
5
Confusion with probability models and intersection of events
Homework Statement I will use an example to showcase my confusion: Suppose a person watches show A 2/3 of the time, show B 1/2 of the time, and both show A and show B 1/3 of the time. For a randomly selected day, what is the probability that the person watches only show A? For a randomly...- 5hassay
- Thread
- Confusion Events Intersection Models Probability
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
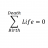
Boundary union and intersection problems
Homework Statement Let A, C \subseteq ℝn with boundaries B(A) and B(C) respectively. Prove or disprove : B(AUC) O B(A)UB(C) and B(A\capC) O B(A)\capB(C) Where O represents each of these symbols : \subseteq, \supseteq, = Homework Equations I know that double inclusion is going to cut the...- STEMucator
- Thread
- Boundary Intersection Union
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-
M
What Is the Torque When the Line of Force Intersects the Center of Rotation?
Homework Statement what is the torque if you know the the line of force intersects the center of the rotation ? Homework Equations The Attempt at a Solution I think the torque will be T= ( f*sin (45) )*d But I'm not sure will there be a torque or not ...the intersection of...- medo_andnino
- Thread
- Intersection Torque
- Replies: 11
- Forum: Introductory Physics Homework Help
-
D
MHB Closed sets intersection of countable open sets
Prove that every closed set in $\mathbb{R}$ is the intersection of a countable collection of open sets. Let $G_n$ be a countable collection of open sets. Then we would have 2 cases either $x\in\bigcap G_n$ which is a point which is closed. Or we could $(a,b)$ in all $G_n$ but how to show that...- Dustinsfl
- Thread
- Closed Intersection Sets
- Replies: 10
- Forum: Topology and Analysis
-
U
Locus of point of intersection of tangents
Homework Statement Locus of the point of intersection of tangents to the parabolas y^{2}=4(x+1) and y^{2}=8(x+2) which are at right angles, is Homework Equations Equation of tangent for first parabola t_{1}y=x+1+at_{1}^{2} Equation of tangent for second parabola t_{2}y=x+2+bt_{2}^{2}...- utkarshakash
- Thread
- Intersection Point
- Replies: 5
- Forum: Precalculus Mathematics Homework Help
-
U
Vectors: Intersection of 2 planes
Homework Statement The question is attached in the picture. The Attempt at a Solution I have found the direction vector of the intersection line, but I have yet to find a point that lies on both planes... I've thought about having \hat{m} and \hat{n} as basis vectors, but i...- unscientific
- Thread
- Intersection Planes Vectors
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-
M
How to Find the Intersection Point of Two Lines in 3D Space
Ive tried finding the intersection point that I labeled I. first try: Because I know the points A and M1 I found |AM1| Then I said |AM1| = |AI| + |IM1| and proceeded to solve and came up with -16 = 2(I1)2 +I2)2 + I3)2) - 10I1 - 8I2 - 3I3 +√(blah blah blah) Second attempt: Law of...- Miike012
- Thread
- Intersection Point
- Replies: 14
- Forum: Calculus and Beyond Homework Help
-
S
Finding the intersection of two functions via linearization
At least I think it's via linearization. Let f(x) = \tan (x^2) - 1 and g(x) = \frac{\ln((x+1)^3)}{3} Find the smallest positive and negative intersection with a relative error of less than 0.001. I don't know. You can linearize one or both, yeah, but you don't have any analytical value to...- srvs
- Thread
- Functions Intersection Linearization
- Replies: 11
- Forum: Calculus and Beyond Homework Help
-
H
Intersection of concave functions
Hi all, I have a question. Suppose f : [ 0, l) \rightarrow ℝ is concave , increasing and continuous where l < ∞ and g : [ 0, l) \rightarrow ℝ is also concave, nondecreasing and continuous on the same interval. Can we claim that f and g intersect finitely many times in this interval (possibly... -
S
Finding line of intersection of two planes
Homework Statement Find parametric equations for the line of intersection of the planes x + y + z = 1 and r = (1, 0, 0) + \lambda(2, 1, 0) + \mu(0, 1, 1) where \lambda, \mu \in R Homework Equations The Attempt at a Solution I attempted to convert the 2nd plane equation to scalar form by...- Spacec0wboy
- Thread
- Intersection Line Planes
- Replies: 25
- Forum: Calculus and Beyond Homework Help
-
S
Find symmetric equations for the line of intersection of the planes
Homework Statement Find symmetric equations for the line of intersection of the planes The planes: 5x - 2y - 2z = 1 4x + y + z = 6 Homework Equations r = r0 + tv x = x0 + at y = y0 + bt z = z0 + ct The Attempt at a Solution I have attempted this in many different manners and would like...- smize
- Thread
- Intersection Line Planes Symmetric
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
L
Intersection of Lines: Solving for Intersection Point using Equations
Homework Statement Show that these lines intersect and what is the intersection point? x=1+t y=2t z=1+3t and x=3s y=2s z=2+s Homework Equations The Attempt at a Solution I don't know how to start, some help please.- Lagrange21
- Thread
- Intersection Lines
- Replies: 5
- Forum: Precalculus Mathematics Homework Help
-
W
Circle-Sphere 3D Intersection Points
I would like to find a way to get the intersection points of a circle and a sphere in 3d. The center of each and their radii are known. This needs to be a general solution so that I can move the center of the sphere in steps and find the intersection at each step. I am curious if this can be...- wb24
- Thread
- 3d Intersection Points
- Replies: 6
- Forum: General Math
-
A
Solving Linear Geometry for a 'projected intersection'
Working on another problem here with varying results. I have three line segments in 3D and am looking to find what would be a projected intersection between two. This projected intersection is defined by a ray that is perpendicular to the axis a and passes through both segments f and s. f...- athuss
- Thread
- Geometry Intersection Linear
- Replies: 1
- Forum: Differential Geometry
-
Y
Tangent Line to Curve of Intersection: Calculating the Normal and Cross Product
Homework Statement Find parametric equations for the tangent line to the curve of intersection of the cone z=√(x2 + 4y2) and the plane 3z = x + 2y + 8 at the point (3,2,5) 2. The attempt at a solution I was trying to make the two Zs equal to each other, and solve for x or y, but I couldn't...- Yitin
- Thread
- Curve Intersection
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
Y
Curve of intersection of a plane and curve
Homework Statement I have to find the slope of the tangent line at (-1,1,5) to the curve of intersection of the surface z = x2 + 4y2 and the plane x = -1 2. The attempt at a solution I really am having trouble figuring out where to start. The question is even numbered, and the only one...- Yitin
- Thread
- Curve Intersection Plane
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
B
Radical of the annihilator is the intersection of associated primes
1. Homework Statement R,M are Noetherian. Prove that the radical of the annihilator of an R-moduleM, Rad(ann(M)) is equal to the intersection of the prime ideals in the set of associated primes of M (that is denoted so regretfully that I am not even allowed to spell it out by the system)...- Barre
- Thread
- Intersection Primes Radical
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
P
Finding the length of an intersection Of 2 planes
Homework Statement Line of intersection between P1: x+y+z=7 and P2:2x-3y-z=-8 crosses the XZ plane at point A and crosses the YZ plane at point B Find the length Of AB Okay so first of all i`m having trouble with understanding crossing the `XZ`plane or `YZ`plane. does this mean that...- Plutonium88
- Thread
- Intersection Length Planes
- Replies: 5
- Forum: Precalculus Mathematics Homework Help
-
A
Union and Intersection of empty class of sets
why intersection of empty class of sets is the whole space while their union is null set? Book writes that an element will fail to be in the intersection if it fails to be in one of the sets of the class but since there is nothing in the empty class so there is nothing in the empty class that...- AAQIB IQBAL
- Thread
- Class Empty Intersection Sets Union
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
W
Sum of Ideals with Empty Intersection
Homework Statement If a ring R contains two ideals B and C with B+C=R and B\capC=0, prove that B and C are rings and R\congB x C. Homework Equations B+C={all b+c|b\inB and c\inC} The Attempt at a Solution So far I've discovered that if the unit of R is in one of the ideals then...- wnorman27
- Thread
- Empty Intersection Sum
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
W
Order of Join and Intersection of Subgroups
Homework Statement If S and T are subgroups of a finite group G, prove that [S:1][T:1] ≤ [S\capT:1][S\veeT:1]Homework Equations Notation: [A:B] is the number of cosets of B in A for some subgroup B of A. note that [A:1] is the order of A. Lagrange's Theorem: For some subgroup S of G...- wnorman27
- Thread
- Intersection
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
O
Question about parameterizing curve of intersection.
I couldn't find any resources in my book or online dedicated to this subject. I honestly don't even know where to begin for this problem. Homework Statement Let f(x,y) = 4 / (1+ x^2 + y^2) and let S be the surface given by the graph of f(x,y) b) Let C2 denote the curve in the xy-plane...- ozone
- Thread
- Curve Intersection
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
B
Parametric Equation intersection and area
Homework Statement Given the curves r=2sin(θ) and r=2sin(2θ), 0 ≤ θ ≤ pi/2, find the area of the region outside the first curve and inside the second curve Homework Equations obviously set up an intersection to see where the two meet, then subtract the circle equation from the rose...- BradyK
- Thread
- Area Intersection Parametric
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

Which equations give nonsense in the intersection of QM and GR?
One of the most frequent questions in this forum is why there is a contradiction between General Relativity and Quantum Mechanics. The most frequent answer is that, in high-energy conditions, some integrals diverge, giving nonsense. I could not find a mention of which integrals one is talking...- nomadreid
- Thread
- Gr Intersection Qm
- Replies: 9
- Forum: Special and General Relativity
-
E
Find cartesian equations of the line of intersection of the planes
Homework Statement Find cartesian equations of the line of intersection of the planes x+3y-6z =2 and 2x+7y-3z=7 The Attempt at a Solution What I did first was I cross product the 2 equation and then I got 33i-9j+k Then I took both of the equation and let y = 0. After that my answer seems...- ezsmith
- Thread
- Cartesian Intersection Line Planes
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
M
How can I get the intersection of these lines
Homework Statement Kindly view my 1st attachment. I need help to get the intersection of the highest line and the line extended by a slope from the horizontal line. Homework Equations y=mx+b y-y1=m(x-x1) The Attempt at a Solution Kindly view my 2nd attachment. By substitution, I...- median27
- Thread
- Intersection Lines
- Replies: 2
- Forum: Engineering and Comp Sci Homework Help
-
T
Linear Algebra- Finding the intersection of two straight lines.
Homework Statement Determine whether the following two lines intersect: (x-2)/2 = (y+3)/1 = (z-4)/-3 ,and (x+3)/4 = (y+4)/1 = (-z+8)/4 Find an intersection point, then find the distance between the lines. Homework Equations Symmetric equations of a...- tcanman
- Thread
- Algebra Intersection Linear Linear algebra Lines straight lines
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
N
The intersection of two varieties, each of which is a complete intersection
Consider f_1,..., f_k, g_1,..., g_l in a polynomial ring C[x_1,...,x_M], where f_i's are homogeneous of degree 2 while g_j's are linear polynomials. Suppose the codim of the variety cut out by S_1 = {f_1,..., f_k} is k while the codim of the variety cut out by S_2 = {g_1,..., g_l} is l...- naturemath
- Thread
- Complete Intersection
- Replies: 2
- Forum: General Math
-
A
Product of gradients at intersection of null clines in 2D system
Hi all, it seems that there is a rule of thumb used by some researchers looking at nonlinear systems whereby they determine the stability of fixed points based on the product of the gradients of the null clines at the point where they intersect. in particular if the product of the gradients...- Appaloosa
- Thread
- 2d Intersection Product System
- Replies: 1
- Forum: General Math
-
C
How to find the intersection of complex roots, Im(z) and Re(z)?
Homework Statement (a) Find the 6th complex roots of √3 + i. (b) Let A={z|z^6 =√3+i} and B={z|Im(z)>0} and C={z|Re(z)>0}. Find A ∩ B ∩ C. Homework Equations z^6=2(cos(π/6)+isin(π/6)) r^6=2, r=2^1/6 6θ=π/6+2kπ, θ=π/36+kπ/3 The Attempt at a Solution I've done part (a): When k=0, z =...- Cottontails
- Thread
- Complex Intersection Roots
- Replies: 4
- Forum: Precalculus Mathematics Homework Help
-

Finding Tangent and Intersection for Parametric Curve
Homework Statement A curve is defined by the parametric equations: x = 2t^3 y = 2t^2 t =/ 0 1)Prove that the equation of the tangent at the point with parameter t is 2x - 3ty + 2t^3 = 0. Proven, and I've no problem with this part. 2.)The tangent at the point t = 2 meets the curve...- Seydlitz
- Thread
- Curve Intersection Parametric Tangent
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
T
Probabillity of an event happening given union and intersection
Hello everyone.. I'm stuck on this and don't really know what equations to apply or how you get the answer. An and Kat go on each Friday to the cinema independently of each other. On any given Friday the probability of both going to the cinema is 1/3. And the probability that at least one of...- thisischris
- Thread
- Intersection Union
- Replies: 4
- Forum: Precalculus Mathematics Homework Help
-
V
Intersection of vector and triangle side
Homework Statement I have a triangle with given vertices ABC. Given a vector that starts from A and intersects side BC, how can I find the point of intersection, p? Thanks Homework Equations The Attempt at a Solution- virusys
- Thread
- Intersection Triangle Vector
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
D
Vectors - Finding a point of intersection
Homework Statement The line L is parallel to the vector 3i - 2j -2k and passes through the point P (1,0,-1/2) find the point of intersection Q of the line L with the plane ∏ x+y+z=2 The Attempt at a Solution I'm completely stumped with this, don't know where to start... I thought...- dimens
- Thread
- Intersection Point Vectors
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
C
How Do You Calculate the Launch Angle for Intersection of Two Moving Objects?
Homework Statement Ok, I need to find the angle at which I will throw an object (O1) so that it intersect with another one (O2) already in motion. I know the speed of each object (constant speed, no acceleration), I know the angle of O2 and its distance from me at time=0 Homework...- cloj63
- Thread
- Intersection
- Replies: 2
- Forum: Introductory Physics Homework Help
-
D
Parametrizing Intersection of Cylinder and Plane
Homework Statement Let C be a cylinder of radius 1. It is cut by the x-y plane from below, and by the plane z-x=1 above. Parametrize all the surfaces of the cylinder. Find a unit normal (pointing outward) for each surface. Homework Equations Equation for a cylinder: x^2+y^2=1 Equation of the...- dbkats
- Thread
- Cylinder Intersection Plane
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
C
Finding the equation of the intersection
Homework Statement Plane 1:2x-3y+8z=7 Plane 2:x-8y+z=14 Plane 3:5x-14y+17z=28 Homework Equations N/A The Attempt at a Solution I took plane 1 and subtracted (plane 2)x2 to get 13y+6z=-21 (I will refer to this as equation 1) Then I took (plane 2)x5 and subtracted plane 3 to get...- cdot9
- Thread
- Intersection
- Replies: 1
- Forum: Precalculus Mathematics Homework Help
-
P
Proof involving functions and intersection
Prove that f(\cap T_\alpha)=\cap f(T_\alpha) for all choices of (T_\alpha) \alpha \in \lambda if and only if f is one-to-one. I've been working on this on and off for a day and have nothing to show for it... Any help pointing me in the right direction would be appreciated. Also, more...- PCSL
- Thread
- Functions Intersection Proof
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
T
Calculating Speed Along Sides of Right Angle at Intersection with Ruler
Homework Statement A right-angle is drawn on a sheet of paper. A ruler , which always remains perpendicular to the bisectrix of this angle moves over the paper with a speed 10cm/sec. The ends of the ruler intersect the sides of the angle. What are the speeds along the sides of the angle of...- teddyayalew
- Thread
- Intersection Points Speed
- Replies: 1
- Forum: Introductory Physics Homework Help
-
S
What is the equation for the circle formed by the intersection of two spheres?
Homework Statement In the space, consider the sphere S1 of radius 3 whose center is the point A (1, -1, 1) and the sphere S2 of radius 2 whose center is the point B(t, 1 - t, 1 + t). a. Find the range of values of t in order the two spheres S1 and S2 have common points b. Find the value of...- songoku
- Thread
- Intersection Spheres
- Replies: 4
- Forum: Precalculus Mathematics Homework Help
-
S
Solving Intersection Curve at (1,1,1): Derivatives & Tangent Line
Homework Statement Given that near (1,1,1) the curve of intersection of the surfaces x^4 + y^2 + z^6 - 3xyz = 0 and xy + yz + zx - 3z^8 = 0 has the parametric equations x = f(t), y = g(t), z = t with f, g differentiable. (a) What are the values of the derivatives f'(1), g'(1)? (b)...- s3a
- Thread
- Curve Derivatives Intersection Line Tangent Tangent line
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
P
Dimension of an intersection between a random subspace and a fixed subspace
I've been struggling with this problem for about two weeks. My supervisor is also stumped - though the problem is easy to state, I don't know the proper approach to tackle it. I'd appreciate any hints or advice. Let V be an random k-dimensional vector subspace of ℝn, chosen uniformly over...- Petawa
- Thread
- Dimension Intersection Random Subspace
- Replies: 4
- Forum: Set Theory, Logic, Probability, Statistics
-
M
Product of two subgroups and intersection with p-subgroup
Let G be a finite group. P is a Sylow p-subgroup of G and K is normal in G also H is a subgroup of G with (|K|,|H|)=1. 1) If p divides |H| then P\capHK is a subgroup of H. 2) Is (1) when K is not normal in G. This is my try of (1); Let y be an element of P\capHK, --> |y| divides...- moont14263
- Thread
- Intersection Product
- Replies: 1
- Forum: Linear and Abstract Algebra
-
I
Intersection of Rationals and (0 to Infinity)?
Homework Statement Let A = [Q\bigcap(0,\infty)] \bigcup {-1} \bigcup(-3, -2] Homework Equations So A = (0,\infty) \bigcup{-1} \bigcup(-3,-2] The Attempt at a Solution I understand that the Rational numbers are cardinally equivalent to (0,\infty), but why isn't...- IntroAnalysis
- Thread
- Infinity Intersection
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
L
Closed set as infinite intersection of open sets
This is not a homework problem, just something I was thinking about. In a general metric space, is it true that every closed set can be expressed as the intersection of an infinite collection of open sets? I don't really know where to begin. Since the finite intersection of open sets is open...- lonewolf5999
- Thread
- Closed Infinite Intersection Set Sets
- Replies: 4
- Forum: Topology and Analysis
-
T
Linear Algebra: intersection of subspaces
Homework Statement I'm working on a problem that involves looking at the dimension of the intersection of two subspaces of a vector space. Homework Equations M \subset V N \subset V dim(M \cap N) [\vec{v}]_{B_M} is the coordinate representation of a vector v with respect to the...- TheTangent
- Thread
- Algebra Intersection Linear Linear algebra Subspaces
- Replies: 2
- Forum: Calculus and Beyond Homework Help