Path integral Definition and 172 Threads
-
O
B How does light have energy to follow infinite paths?
A recent Veritasium video demonstrates via experiment that light from a laser pointer takes every possible.path from source to destination, as promulgated by Richard Feynman. These paths need not be straight lines and thus can wander all of spacetime. That implies light is taking an infinite, or...- oknow
- Thread
- Feynman Path integral Photons
- Replies: 6
- Forum: Quantum Physics
-
Y
A Lagrangian in the Path Integral
Using free scalar field for simplicity. Hi all, I have a question which is pretty simple, we have the path integral in QFT in the presence of a source term: $$ Z[J] = \int \mathcal{D}\phi \, e^{i \int d^4x \left( \frac{1}{2} \phi(x) A \phi(x) + J(x) \phi(x) \right)} $$ So far so good. Now...- YeaNah
- Thread
- Lagrangian Path integral Quantum field theory
- Replies: 13
- Forum: Quantum Physics
-
A
I What do the authors of the paper mean here exactly by path integral?
Hi, I am new here so apologies if i am not using the right subforum. I don't have a physics background so i am not very technical but i do have a little bit of understanding. I was reading this paper by hawking/hertog and came across something that ended up confusing me. Here is it: "Pre-big...- Andrewmiller5432
- Thread
- Cosmology Path integral Quantum cosmology Quantum mechanics Stephen hawking
- Replies: 6
- Forum: Quantum Physics
-

I What maps are considered in the Polyakov path integral?
Recently I've came to some references on mathematical aspects on string theory that deal with the Polyakov euclidean path integral. An example is the book "Quantum Fields and Strings: A Course for Mathematicians. Volume 2", where it is stated roughly that the path integral is $$A =...- GeniVasc
- Thread
- Mapping Path integral Polyakov String theory
- Replies: 0
- Forum: Beyond the Standard Models
-
G
Computing path integral with real and Grassmann variables
The first step seems easy: computation of the $\theta$ and $\overline{\theta}$ integrals give $$Z[w] = \frac{1}{(2\pi)^{n/2}}\int d^n x \: \det(\partial_j w_i(x)) \exp{\left(-\frac{1}{2}w_i(x)w_i(x)\right)}.$$ From here, I tried using that $$\det(\partial_j w_i (x)) = \det\left(\partial_j w_i...- Geigercounter
- Thread
- Computing Grassmann Integral Path Path integral Qft Variables
- Replies: 1
- Forum: Advanced Physics Homework Help
-
A
Is the Result of the Path Integral Positive Due to Negative dx?
In the book it is mentioned that, in path c, the line integral would be: $$\int \vec{F}\cdot \vec{dr} = A \int_{1}^{0}xy dx = A\int_1^0 x dx = -\dfrac{A}{2}$$. but I think that dx is negative in that case, the result would be positive, right?- Ark236
- Thread
- Exercise Integral Path Path integral
- Replies: 10
- Forum: Introductory Physics Homework Help
-
T
A Grassmann number: a more rigorous treatment?
Most textbooks on fermionic path integral only briefly introduce Grassmann numbers. However, I want a more systematic treatment to feel comfortable about this approach. For illustration, I have several examples here. Example 1: Consider a system with only one state, how to calculate ##\langle...- taishizhiqiu
- Thread
- Fermions Grassmann Path integral Rigorous Treatment
- Replies: 11
- Forum: Quantum Physics
-
G
I Can a Path Integral Formulation for Photons Start from a Massless Premise?
I am aware that one usually starts from the Maxwell equations and then derives the masslessness of a photon. But can one do it the other way round? The action of photon would be ##S = \hbar \int \nu (1 - \dot{x}^2) \mbox{d}t##, where ##\nu## is the frequency acting as a Lagrange multiplier...- gerald V
- Thread
- Integral Path Path integral Photon
- Replies: 3
- Forum: Quantum Physics
-
A Orthogonality of variations in Faddev-Popov method for path integral
Hi there, I've been stuck on this issue for two days. I'm hoping someone knowledgeable can explain. I'm working through the construction of the quantum path integral for the free electrodynamic theory. I've been following a text by Fujikawa ("Path Integrals and Quantum Anomalies") and also...- Wizard
- Thread
- Integral Method Orthogonality Path Path integral Path integral formulation Quantum electrodynamics Quantum field theory
- Replies: 1
- Forum: Quantum Physics
-
K
I Feynman path integral and events beyond the speed of light
In Richard Feynman's book "The Strange Theory of Light and Matter", in chapter 2, he explains how to calculate the probability that light from some source will be reflected by a mirror and be detected at some location. He explains how you sum up all of the probability amplitudes (represented...- kurt101
- Thread
- Events Feynman Integral Light Path Path integral Speed Speed of light
- Replies: 57
- Forum: Quantum Physics
-
I Understanding how to derive the Feynman rules out of the path integral
I am studying interacting scalar fields (from Osborn) using the path integral approach. We define the functional integral \begin{equation*} Z[J] := \int d[\phi] e^{iS[\phi] + i\int d^d x J(x) \phi(x)} \tag{1} \end{equation*} The idea is to differentiate ##Z[J]## with respect to ##J## and end...- JD_PM
- Thread
- Derive Feynman Feynman rules Integral Path Path integral Rules
- Replies: 33
- Forum: Quantum Physics
-
M
The propagator of eigenstates of the Total Angular Momentum
To show that when ##[J^2, H]=0 ## the propagator vanishes unless ##j_1 = j_2## , I did (##\hbar =1##) $$ K(j_1, m_1, j_2 m_2; t) = [jm, e^{-iHt}]= e^{iHt} (e^{iHt} jm e^{-iHt}) - e^{-iHt} jm $$ $$ = e^{iHt}[jm_H - jm] $$ So we have $$ \langle j_1 m_1 | [jm, e^{-iHt} ] | j_2 m_2 \rangle $$ $$ =...- mathsisu97
- Thread
- Angular Angular momemtum Angular momentum Eigenstates Feynman propagator Momentum Path integral Propagator Spin total angular momentum
- Replies: 9
- Forum: Advanced Physics Homework Help
-

A Where did this term in the path integral come from?
I'm trying to derive the path integrals, but this step got me confused: Consider the propagator $$K_{q_{j+1},q_j}=\langle q_{j+1}|e^{-iH\delta t}|q_j\rangle $$ Knowing that ##\delta t## is small, we can expand it as $$K_{q_{j+1},q_j}=\langle q_{j+1}|(1-iH\delta t-\frac 1 2 H² \delta...- PORFIRIO I
- Thread
- Integral Path Path integral Term
- Replies: 1
- Forum: Quantum Physics
-

A Derive the Principle of Least Action from the Path Integral?
Several weeks ago I had considered the question as to how one can start from the Schroedinger Equation, and after several transformations, derive F=ma as a limiting case. At some point in my investigations of this derivation, it occurred to me that this is simply too much work. While in...- hyksos
- Thread
- Derive Integral Least action Path Path integral Path integral formulation Principle
- Replies: 5
- Forum: Quantum Physics
-

A Functional Determinant of a system of differential operators?
So in particular, how could the determinant of some general "operator" like $$ \begin{pmatrix} f(x) & \frac{d}{dx} \\ \frac{d}{dx} & g(x) \end{pmatrix} $$ with appropriate boundary conditions (especially fixed BC), be computed? And assuming that it diverges, would it be valid in a stationary...- Yellotherephysics
- Thread
- Determinant Differential Functional Functional analysis Operators Path integral Path integral formulation Path integrals System
- Replies: 2
- Forum: Quantum Physics
-

B What Is the Occurrence Rate of Path Integral in a Photon Double-Slit Experiment?
Hi forgive my very ignorant question. How frequently does 'Path Integral', curved shot and normal shot happen out of say 100 shots with a photon?- HexHammer
- Thread
- Integral Path Path integral
- Replies: 6
- Forum: Quantum Physics
-
S
A Does Feynman's path integral ignore alternative histories?
Summary: Does Richard Feynman's multiple histories ignore alternative histories? Did Richard Feynman's multiple histories (https://en.wikipedia.org/wiki/Multiple_histories) ignore the existence of other alternarive histories or paths? I ask this referring to this comment from this page...- Suekdccia
- Thread
- Feynman Integral Many worlds interpretation Path Path integral Quantum mechanics
- Replies: 1
- Forum: Quantum Interpretations and Foundations
-
E
I About the Feynman Path Integral and Principle of Least Time
I don't entirely get why we usually say that only the shortest path contributes in the path integral. If you calculate the volume of nth fresnel zones which is the locus where the path length is between n-1 and n wavelengths from the shortest path in 3 dimensions, they are the same I believe. So...- EsbMtrx
- Thread
- Feynman Integral Path Path integral Principle Time
- Replies: 1
- Forum: Quantum Physics
-
W
A Path Integral Approach To Derive The KG Propagator
I'm having trouble understanding a specific line in my lecturers notes about the path integral approach to deriving the Klein Gordon propagator. I've attached the notes as an image to this post. In particular my main issue comes with (6.9). I can see that at some point he integrates over x to...- Woolyabyss
- Thread
- Approach Derive Integral Path Path integral Path integral formulation Propagator Quantum field theory
- Replies: 4
- Forum: Quantum Physics
-

I Counterpart of Feynman integral in de Broglie-Bohm theory
I am looking for good references / clarifications on the subject. First of all, my question is concerned only with mathematical formulation of something that sort of plays the role of the Feynman path integral of the "standard" QFT. It is not concerned with the physical or philosophical...- ErikZorkin
- Thread
- Bohmian mechanics Feynman Integral Mathematical Path integral Quantum field theory Theory
- Replies: 22
- Forum: Quantum Interpretations and Foundations
-

A Question about equivalence of Path Integral and Schrodinger
I've seen a proof that the path integral formulation of quantum mechanics is equivalent to solving Schrodinger's equation. However, it appears to me that the proof actually depended on the Hamiltonian having a particular form. I'm wondering how general is the equivalence. Let me sketch a...- stevendaryl
- Thread
- Equivalence Integral Path Path integral Path integral formulation Schrödinger
- Replies: 19
- Forum: Quantum Physics
-
S
I QFT Path Integral: Confusions on Left & Right Most Terms & Vacuum State
Hello! I am reading from Schwarz book on QFT the Path Integral chapter and I am confused about something. I attached a SS of that part. So we have $$<\Phi_{j+1}|e^{-i\delta H(t_j)}|\Phi_{j}>=N exp(i\delta t \int d^3x L[\Phi_j,\partial_t \Phi_j])$$ What happens when we have the left and right...- Silviu
- Thread
- Integral Path Path integral Qft
- Replies: 12
- Forum: High Energy, Nuclear, Particle Physics
-
H
A How to evaluate path integrals numerically?
Since we only know Gaussian integration, could one get Green's function numerically with interacting action. Usual perturbation theory is tedious and limited, could one get high accurate result with PC beyond perturbation?- howl
- Thread
- Integrals Path Path integral Path integrals
- Replies: 12
- Forum: Atomic and Condensed Matter
-

Path Integral Setup for Given Initial and Final Points
Homework Statement The path integral from (0,0,0) to (1,1,1) of $$<x^2,2yz,y^2>$$. I am a little confused about the setup.Homework Equations $$\int_{a}^{b} v.dl$$The Attempt at a Solution Here is how I set it up. $$\int_{0}^{1}x^2 dx + \int_{0}^{1}2yz dy + \int_{0}^{1}y^2 dz$$ Since the...- Safder Aree
- Thread
- Calculus Integral Multivariable calculus Path Path integral Physics
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-

I Is the Action Always a Minimum in the Principle of Least Action?
Hello, When we applying the principle of least action, we require ##\delta S=0##, which corresponding to the action S being an extremum. I am just wondering why do we say that the action is a minimum instead of a maximum for a physical path? Can I use the path integral to explain this problem...- BookWei
- Thread
- Classical mechanics Least action Path integral Principle
- Replies: 3
- Forum: Classical Physics
-

I Proof of Kaku (8.18): Completing the Square and Using Spiegel's Result
In the following there is a proof, for positive values of ##a## only, of (8.18) of Kaku, reference 1, I quote' $$\int_{-\infty}^\infty~\mathrm{d}p~e^{iap^2+ibp}=\sqrt \frac{i\pi}{a}e^{-ib^2/4a}~~~~~~~~~~~~~(8.18)$$ '. Kaku says this result can be proved by completing the square. $$iap^2+ibp =...- rocdoc
- Thread
- Path integral Proof Quantum field theory Quantum theory
- Replies: 12
- Forum: Quantum Physics
-
J
A Path Integral of a Spontaneously Broken Theory
A scalar field theory with potential $$V(\phi)=-\mu^2\phi^2+\lambda \phi^4$$ is spontaneously broken and as a consequence, for the ground state, $$\langle \phi(x) \rangle \neq 0$$. However, the path integral, which should give ground state expectation values, looks to be zero by oddness of the...- JRudolfo
- Thread
- Broken Integral Path Path integral Theory
- Replies: 15
- Forum: Quantum Physics
-

I Feynman Path Integral: Teaching and Questions
I'm reading "Teaching Feynman’s sum-over-paths quantum theory" by Taylor et al. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.374.4480&rep=rep1&type=pdf, I'd like to confirm whether my understanding is correct, so a couple of questions. 1. We need to try and think of all kinds of...- Swamp Thing
- Thread
- Feynman Integral Path Path integral
- Replies: 8
- Forum: Quantum Physics
-
F
I Does the path Integral contain virtual particles?
So Feynman's path integral considers every possible path that a particle could take from start to end. In that process, there would be a path which contains a segment from, say, A to B at time t. But there could also be a path with a segment from B to A at that same time, t. If so, would this...- friend
- Thread
- Integral Particles Path Path integral Virtual Virtual particles
- Replies: 21
- Forum: Quantum Physics
-
Y
I Why isn't path integral of H-field 0?
So for an infinite plane of current, current traveling in the X direction, the magnetic field everywhere above the plane is going clockwise, and the m. field below the plane is going counterclockwise. So the path integral is Integral of H dot dl = Current Enclosed Why, in this video, does the...- yosimba2000
- Thread
- Integral Path Path integral
- Replies: 2
- Forum: Other Physics Topics
-
C
Inelastic collision and the sum of internal forces
Homework Statement Suppose I have a system which contains two bodies m1 and m2 with initial velocities v1 and v2 , respecitvely. they hurl toward each other and make an inelastic collision. such that they are now one body of mass m1 + m2 I know that the difference in momentum is...- CGandC
- Thread
- Collision Energy Forces Inelastic Inelastic collision Internal Internal forces Momentum and energy Path integral Sum Work
- Replies: 6
- Forum: Introductory Physics Homework Help
-

I Checking My Understanding: Lagrangian & Path Integral Formulation
I note the following: \begin{equation} \begin{split} \langle \vec{x}| \hat{U}(t-t_0) | \vec{x}_0 \rangle&=\langle \vec{x}| e^{-2 \pi i \frac{\mathcal{H}}{\hbar} (t-t_0)} | \vec{x}_0 \rangle \\ &=e^{-2 \pi i \frac{\mathcal{H}}{\hbar} (t-t_0)} \delta(\vec{x}-\vec{x}_0)...- redtree
- Thread
- Dirac delta function Hamiltonian Integral Lagrangian Path Path integral Path integral formulation Propagator
- Replies: 6
- Forum: Quantum Physics
-
S
I Path Integral in QM: Resolving Confusion on Causality
Hello! I am reading a derivation of the path formulation of QM and I am a bit confused. They first find a formula for the propagation between 2 points for an infinitesimal time ##\epsilon##. Then, they take a time interval T (not infinitesimal) and define ##\epsilon=\frac{T}{n}##. Then they sum...- Silviu
- Thread
- Integral Path Path integral Qm
- Replies: 1
- Forum: Quantum Physics
-

A Help to understand the derivation of the solution of this equation
Please, help here people. Im reading this article Wave Optics in Gravitational Lensing (T. T. Nakamura, 1999) . In the article start work with \begin{equation} (\nabla ^2 +\omega)\tilde\phi = 4\omega^2U\tilde\phi \end{equation} where $$\tilde\phi = F(\vec r)\tilde\phi_{0}(r)$$. Using...- needved
- Thread
- Derivation General relativity Gravitational waves Path integral Path integral formulation
- Replies: 1
- Forum: Special and General Relativity
-
J
Flux-flux correlation function under Feynman's path integral
This is a chemically inspired problem, but the path is fully quantum mechanics and a bunch of integrals. How does one calculate fully quantum mechanical rate ($\kappa$) in the golden-rule approximation for two linear potential energy surfaces? Attempt: Miller (83) proposes...- junt
- Thread
- Correlation Correlation function Feynman propagator Function Integral Path Path integral Physical chemistry Quantum chemistry Quantum mechaincs Reaction mechanism
- Replies: 2
- Forum: Quantum Physics
-
S
Quantum Where Can I Find Resources on Path Integral Formulation in Quantum Mechanics?
Hello! Can someone suggest me a good reading about path integral formulation of quantum mechanics? I took 2 undergrad courses on QM, so I would like something focusing on path integral (maybe some problems too). I don't necessary want a book, even some online pdf that contains some good...- Silviu
- Thread
- Integral Path Path integral Path integral formulation
- Replies: 2
- Forum: Science and Math Textbooks
-
J
I Difference between statistical and dynamical properties
Hi All, What are the main differences between statistical and dynamics properties in physics? Could you please explain the difference for problems in both classical and quantum mechanics. For instance, path integral molecular dynamics is supposed to give statistical properties of a quantum...- junt
- Thread
- Classical mechanics Difference Molecular dynamics Path integral Properties Quantum mechancis Schrodinger equation Statistical
- Replies: 4
- Forum: Quantum Physics
-
F
A On the equivalence of operator vs path integral in QFT
I have read many textbooks and googled google times for a clear explanation, but I could not find one. How does raising and lowering -annihilation/ creation-(is that energy or particle number?) translate to transition probabilities of path integral.- ftr
- Thread
- Equivalence Integral Operator Path Path integral Qft Quantum field theory
- Replies: 15
- Forum: Quantum Physics
-
A Path integral formula for a state with non-trivial time dependency
Consider a system with a time-dependent Hamiltonian. We know that the evolution of the state of this system, is given by ## \displaystyle |\Psi(t_1)\rangle=T \exp\left( -i \int_{t_0}^{t_1} dt H(t) \right) |\Psi(t_0)\rangle ##. Do you think you can prove that the path integral formula for the...- ShayanJ
- Thread
- Formula Integral Path Path integral State Time
- Replies: 14
- Forum: Quantum Physics
-
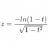
I Path integral implies superluminal motion?
In the path integral formalism, where we treat a photon as if it takes every possible path, aren't the possible paths limited by the speed of light? If we were to perform the double slit experiment, and shield the detector after a specified time frame to limit the time for a photon to make the...- substitute materials
- Thread
- Integral Motion Path Path integral Superluminal
- Replies: 16
- Forum: Quantum Physics
-
A Path integral formula for vacuum to vacuum amplitude
I'm reading the path integral chapter of Schwartz's "Quantum Field theory and the Standard model". Something seems wrong! He starts by putting complete sets of states(field eigenstates) in between the vacuum to vacuum amplitude: ## \displaystyle \langle 0;t_f|0;t_i \rangle=\int D\Phi_1(x)\dots...- ShayanJ
- Thread
- Amplitude Formula Integral Path Path integral Vacuum
- Replies: 1
- Forum: High Energy, Nuclear, Particle Physics
-
A Ground state wave function from Euclidean path integral
From the path integral approach, we know that ## \displaystyle \langle x,t|x_i,0\rangle \propto \int_{\xi(0)=x_i}^{\xi(t_f)=x} D\xi(t) \ e^{iS[\xi]}##. Now, using ## |x,t\rangle=e^{-iHt}|x,0\rangle ##, ## |y\rangle\equiv |y,0\rangle ## and ## \sum_b |\phi_b\rangle\langle \phi_b|=1 ## where ## \{...- ShayanJ
- Thread
- Euclidean Function Ground Ground state Integral Path Path integral State Wave Wave function
- Replies: 12
- Forum: Quantum Physics
-
S
I Vanishing Hamiltonian for quantum path integral
The path integral in quantum mechanics involves a factor ##e^{iS_{N}/\hbar}##, where ##S_{N}\equiv \sum\limits_{n=1}^{N+1}[p_{n}(x_{n}-x_{n-1})-\epsilon H(p_{n},x_{n},t_{n})].## In the limit ##N \rightarrow \infty##, ##S_{N}## becomes the usual action ##S## for a given path.When the...- spaghetti3451
- Thread
- Hamiltonian Integral Path Path integral Quantum
- Replies: 2
- Forum: Quantum Physics
-
A
I Path integral and causally disconnected parts of universe....
One more question: it appears that portions of the universe are expanding away from us faster than the speed of light. Given this, particles in two 'parts' of the universe that are no longer causally connected should not be able to influence each other (due to speed of light constraint). So...- asimov42
- Thread
- Integral parts Path Path integral Universe
- Replies: 6
- Forum: Quantum Physics
-
S
A Path integral computes time-ordered products
In general, ##\displaystyle{\langle q_{f}|e^{-iHt/\hbar}|q_{i}\rangle=\int\mathcal{D}q(t)\ e^{iS[q]/\hbar}}## and ##\displaystyle{\langle q_{f}|\hat{Q}(t)|q_{i}\rangle=\int\mathcal{D}q(t)\ e^{iS[q]/\hbar}}\ q(t).##How can one switch from the above expressions to the following...- spaghetti3451
- Thread
- Integral Path Path integral
- Replies: 1
- Forum: Quantum Physics
-
S
A Utility of path integral formulation of quantum mechanics
How does the path integral formulation of quantum mechanics as given by ##\langle q_{f}|e^{-iHt/\hbar}|q_{i}\rangle = \int \mathcal{D}q(t)\ e^{iS[q]/\hbar}## make manifest aspects of quantum mechanics such as symmetries?- spaghetti3451
- Thread
- Integral Mechanics Path Path integral Path integral formulation Quantum Quantum mechanics Utility
- Replies: 12
- Forum: Quantum Physics
-
A
I Field eigenstates and path integral formulation
Recently I have reviewed by reference books to get a better understanding of the fundamentals of QFT and there is one thing I still do not understand. In the QFT derivation of the path integral formula, it seems that every book and online resource makes the assumption that for the field operator...- Alhaurin
- Thread
- Eigenstates Field Integral Path Path integral Path integral formulation
- Replies: 4
- Forum: Quantum Physics
-
C
A Where to start with path integral Monte Carlo?
Trying to accomplish a monte carlo simulation on the condensed state of 4He, yet I am in my sophomore year and know only a bit of quantum statistical physics. Is there any documentations recommended for beginners to the algorithm applied to 4He? I've found some but they are not friendly to...- common_2012
- Thread
- Helium Integral Monte carlo Monte carlo simulation Path Path integral Simulation Statistical mechanics
- Replies: 1
- Forum: Quantum Physics
-
D
Comparing Path Integral Conventions in QED
Hello. I am doing some reading on QED and am getting a bit confused on the different conventions used. In Matthew Schwartz's book we have the Lagrangian given as: LQED = -¼ FμνFμν + iψ*γμ(∂μ + ieAμ)ψ - V(ψ*ψ) And the path integral factor is exp(iS). In another text, however, I see the QED...- dman12
- Thread
- Integral Path Path integral
- Replies: 3
- Forum: High Energy, Nuclear, Particle Physics
-
T
Why Do Path Integrals Involve Multiple Integrations Instead of Simple Summation?
Source: http://web.mit.edu/dvp/www/Work/8.06/dvp-8.06-paper.pdf Regarding page 5 of 14, I don't understand the multiple integrals thing. Ain't we supposed to sum up all the paths like in this equation (4) but why do they instead multiply and integrate over integration and so on?Also for...- TimeRip496
- Thread
- Integral Path Path integral Path integral formulation
- Replies: 8
- Forum: Quantum Physics