What is Proofs: Definition and 698 Discussions

A mathematical proof is an inferential argument for a mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use other previously established statements, such as theorems; but every proof can, in principle, be constructed using only certain basic or original assumptions known as axioms, along with the accepted rules of inference. Proofs are examples of exhaustive deductive reasoning which establish logical certainty, to be distinguished from empirical arguments or non-exhaustive inductive reasoning which establish "reasonable expectation". Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in all possible cases. An unproven proposition that is believed to be true is known as a conjecture, or a hypothesis if frequently used as an assumption for further mathematical work.Proofs employ logic expressed in mathematical symbols, along with natural language which usually admits some ambiguity. In most mathematical literature, proofs are written in terms of rigorous informal logic. Purely formal proofs, written fully in symbolic language without the involvement of natural language, are considered in proof theory. The distinction between formal and informal proofs has led to much examination of current and historical mathematical practice, quasi-empiricism in mathematics, and so-called folk mathematics, oral traditions in the mainstream mathematical community or in other cultures. The philosophy of mathematics is concerned with the role of language and logic in proofs, and mathematics as a language.

View More On Wikipedia.org
Recent contents Top users
  1. S

    Understanding the Sign Convention for Lens Formula Proofs

    I googled for lens formula's proof on the internet and found one here http://www.tutorvista.com/content/physics/physics-ii/light-refraction/convex-lens-formula.php The problem is that during the course of derivation, it is assumed that image distance is -u following the sign convention...
  2. A

    MHB Proofs on growth rates of functions theorems using definition of a limit

    Hello, I am working through some proofs from the following document: Function Definitions Under Calculation of Big - Oh, some theorems are provided that classify the growth rates of functions in relation to one depending on what the limit is as the input approaches infinity. One proof is...
  3. C

    Two Group homomorphism proofs

    Homework Statement Let ##\theta : G \mapsto H## be a group homomorphism. A) Show that ##\theta## is injective ##\iff## ##\text{Ker}\theta = \left\{e\right\}## B) If ##\theta## is injective, show that ##G \cong I am \theta ≤ H##. The Attempt at a Solution A)The right implication is...
  4. marellasunny

    Analytical proofs in mathematical papers

    I am writing my first paper in applied mathematics.I would like to know how important is it to write a analytical proof for the numerical solutions arrived?I always thought these sort of things were left to the 'pure mathematicians' and one didn't need to bother.As a engineer,I was always used...
  5. H

    Proofs of dimensions and subspaces check

    Hi, I'd be grateful if someone could tell me whether these proofs I've done are correct or not. Thanks in advanced. Let V be an n-dimensional vector space over \mathbb{R} Prove that V contains a subspace of dimension r for each r such that 0 \leq r \leq n Since V is n-dimensional...
  6. Astrum

    Having Trouble With Mathematical Proofs - How Important for Physics?

    I'm having a lot of difficulty with proofs. I can understand them when I read them, but when asked to prove things myself, I usually fall flat on my face. How important are proofs for physics? Do I really need an intimate understand of the mathematics, or would that be irrelevant? I was...
  7. A

    Relativity question involving proofs of beta and gamma

    Homework Statement (a) The ratio v/c is very often denoted by the single symbol β. Show that if β<<1, the following are valid through terms of order β^2 E = mc^2 + (mv^2)/2 = (mc^2)[1+(β^2)/2] K = (mv^2)/2 = (mc^2)[(β^2)/2] pc = mvc = m(c^2)β γ = 1+(β^2)/2 (b) Show that if γ = ε^-1...
  8. H

    Why use stipulations in Epsilon Delta Proofs?

    Homework Statement When constructing an Epsilon Delta proof, why do we need to make a stipulation? For example, in most proofs for limits of quadratic functions, it is stipulated, for example, that δ≤1. Why is this needed anyway? This is my thought process for a quadratic: Prove that lim(x...
  9. A

    How are formulas with inductive proofs discovered?

    There are certain formulas for which only inductive proofs are known. But since we need to know the formula first to prove it using mathematical induction, how do they get the formula in the first place? Here is an example: - Euler's formula in graph theory states that v-e+f=2 for all planar...
  10. S

    MHB Uncovering the Means to Verify Math Proofs

    I feel the question i am going to ask it is one of the most important question ,if not the most important,in Mathematics. And i may add if answered correctly a lot of misunderstanding and useless arguing can be avoided. So here is the question: What are the mathematical means or theories that...
  11. R

    Geometrical (circle) Proofs - Help

    Q1 Two circles intersect at P and Q. Two parallel line segments APC and BQD are drawn to meet one circle at A and C, and the other circle at B and D. PB and PD are diameters of their respective circles. Prove that points B, Q and D are collinear. Q2 AB and CD are two parallel chords of a...
  12. H

    What Are the Proofs for Powers in Normal Subgroups and Orders in Homomorphisms?

    Homework Statement a) Let H be a normal subgroup of G. If the index of H in G is n, show that y^n \in H for all y \in G. b) Let \varphi : G \rightarrow G' be a homomorphism and suppose that x \in G has order n. Prove that the order of \varphi(x) (in the group G') divides n. (Suggestion: Use...
  13. M

    Proficiency in Mathematical Proofs

    Where does one attain the skill/ability (skill vs. ability is a good question in itself) to do proofs? By "do proofs" I mean prove existing theorems. For instance I am really no good with ε-δ proofs. The concept is so easy, but when I have to prove something using ε-δ I either have no idea what...
  14. twoski

    [Proofs] Proof by contraposition

    Homework Statement For n ∈ Z+ prove by contrapositive that if 2n3 + 3n2 + 4n + 5 is odd then n is even. Homework Equations The Attempt at a Solution If n is odd then ( 2n³ + 3n² + 4n + 5 ) is even. By definition, a number n is odd if n = 2k + 1 for some integer k. A number...
  15. twoski

    Proof by Cases: No Solutions for 5x^2 + 4y^3 = 51 | Z+ x, y

    Homework Statement Give a proof by cases to show that the equation 5x^2 + 4y^3 = 51 does not have solutions x, y ∈ Z+ The Attempt at a Solution My wording is very awkward, i am hoping that i can get some advice on it. To prove there are no solutions x, y ∈ Z+ we first...
  16. O

    Multivariable epsilon delta proofs

    Homework Statement lim (x,y) -> (0,0) xy/sqrt(x^2+y^2) = 0 The Attempt at a Solution my understanding of my actual goal here is kind of poor given ε>0 there exist ∂>0 s.t. 0 < sqrt(x^2 + y^2) < ∂ then 0<|f(x,y) - L| < ε | xy/sqrt(x^2 + y^2) - 0 | < ε (xy * sqrt(x^2 + y^2)) /...
  17. B

    Equivalence of Vector Statements: Proofs and Solutions

    Homework Statement Proof that the following statements are all equivalent. First assume that none of the vectors are zero vectors. Then prove it in the degenerate case, where the vectors are zero vectors. 1) u = kv where k is a scalar. 2) u \times v = 0 3) u \cdot v = ||u|| ||v|| 4)...
  18. T

    Is Indirect Proof Easier for Proving Inequality Involving Real Numbers?

    Homework Statement Let x \in ℝ Prove that if 3x^{4}+1≤x^{7}+x^{3}, then x > 0 Homework Equations None The Attempt at a Solution Assume 3x^{4}+1≤x^{7}+x^{3} then 0 ≤ -3x^{4}-1≤x^{7}+x^{3} Then I assumed that each was greater than or equal to 0, which I thought gave the desired...
  19. W

    MHB Can you prove these floor and ceiling equations?

    Hi, i need help with 2 proofs based off of floor and ceiling. 1.)For any real number x, if x is not an integer, then floor(x) + floor(-x) =- 1.2.For all real numbers x, floor(floor(x/2)/2) = floor(x/4). Thanks.
  20. N

    Proofs In Advance Calculus

    I'm a sophomore at Rensselaer Polytechnic Institute and I'm taking MATH 4600 which is Advanced Calculus. I love the class and it is very interesting, we're taking what we learned in Multivariable Calculus, but just at a much higher level. However, my teacher does a lot of proofs behind why...
  21. F

    Sets and functions proofs needed

    Hello there, I am extremely new to mathematical analysis and do not have an idea how to prove the following questions. Could you please give me a hand and show me a way? Let At , t ∈ T, be a family of sets, and let X be a set. Prove the identities...
  22. A

    Proofs for Sets: Expert Help and Tips for Math Homework

    Homework Statement hopefully the writing is readable: http://i.imgur.com/VJ8vN.jpg All three if possible. Homework Equations none The Attempt at a Solution To be completely honest, I missed that whole week of lectures due to personal problems and I've had no chance to talk to an...
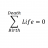
  23. STEMucator

    Proving the Divisibility of Relatively Prime Integers

    Homework Statement I've got two questions out of my textbook. I'll list both of them and my attempts below. (1) Suppose : a, b, c\in Z, a|c \space \wedge \space b|c.\spaceIf a and b are relatively prime, show ab|c. Show by example that if a and b are not relatively prime then ab does not...
  24. A

    Set cardinality, Turing encoding, and inductive proofs

    I'm going to construct an ordered set, and I'd like to ask some questions about it; and in particular consider coding problems about this set and sets in general (Turing tape encoding). Start with: A={ } And, allow a mutable temporary set, initialized with: T={ } and an iterator: set n=0 For...
  25. G

    Doing proofs using the basic properties of numbers, problems

    Homework Statement Prove that if 0 < a < b, then a < √ab < (a + b)/2 < b Homework Equations To prove this use the 12 properties of numbers (commutativity, trichotomy law, associativity, etc...). The Attempt at a Solution The main problem is I don't know if I need to define the...
  26. R

    Cartesian Tensors and some proofs and problems regarding it.

    Homework Statement I am stuck at this point where I have to prove that the kronecker delta is isotropic tensor. Homework Equations δij=δji The Attempt at a Solution I know that to prove this I have to show that under coordinate transfor mation it does not change..but it's a bit...
  27. J

    Can I prove matrix properties using simple steps?

    Homework Statement Homework Equations The Attempt at a Solution -(y, x) = -(YX-XY) = XY-YX Can I do this or would I have to define a matrix X= ( a b c d ) Y= ( e f g h)...
  28. T

    Epsilon delta proofs equaling a constant

    Homework Statement Lim x→a of f(x) = c (Where c is a constant) Homework Equations The Attempt at a Solution I have no idea. I am able to do these if I can manipulate fx-L to equal x-a but I am having trouble with this one. Please help me!
  29. D

    Delta-epsilon proofs (again)

    Homework Statement Prove the following limits using delta-epsilon definition (a)\mathop {\lim }\limits_{x \to 5{}^ - } \sqrt[4]{{5 - x}} = 0 (b)\mathop {\lim }\limits_{x \to 2} ({x^4} - 1) = 15 (c)\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} - 2x}}{{x + 2}} = 3 Homework Equations...
  30. T

    Linear Algebra Proofs: Solving for Scalar and Vector Using Axioms

    Hey all, So I'm just starting a course in linear algebra, but I don't have much experience with proofs. This problem has been giving me some difficulty. So we have a scalar "a" and vector x. V is a linear space, and x is contained in V. I have to show that if ax=0, where 0 is the zero...
  31. D

    Are proofs needed for definitions? Conditional Probability

    My probability class has me wondering about pure math questions now. We started with the axioms and are slowly building up the theory. Everything was fine but then a definition of Conditional Probability P[A|B] = \frac{P[AB]}{P[B]} appeared and it's just not sitting right with me. I know that...
  32. M

    How to correctly format proofs?

    Homework Statement Hi, I'm taking a mathematical proofs class and I'm having trouble formatting my proofs correctly. We haven't done any proofs in class yet, but some simple proofs are due in this week's homework assignment. I've tried using the internet to help me, but all the hits that I get...
  33. N

    Proof Theorems: Learn How to Make Proofs | Beginner's Guide

    Hi everyone! I'm a new user of this forum! I was interested in learning to make proofs of the various theorems. Is there a schematical way to make the proofs ? Where should i start ? And what are the statement for my proofs that are absolutely true so that i can base my proof on ? Is there...
  34. S

    Need help understanding Linear algebra proofs (and linear algebra in general)

    Hey all, I am trying to get a head start on Linear Algebra before i start taking classes in a couple weeks. I am about to go into my second year undergraduate and all i have behind my belt is calculus (single varialbe, multivariable, and vector analysis (curl, divergence, etc)). I am...
  35. X

    Logical proofs: Empirical evidence for constant gravity in the past and future

    Hello everyone. I'm a first time poster, but a long time lurker. I don't have a degree in physics, but I have always held the discipline and all its branches, near to my heart. A little background on the question. I got into an argument with a friend of mine about faith in religion and faith...
  36. C

    MHB SE Maths - Teaching with Proofs: Expert Tips for Secondary Education

    In online maths fora we often see posts like the first post in thttp://www.mathhelpboards.com/f15/book-recommendations-proofs-1649/#post7709 from kanderson. When I was in secondary education and then an undergraduate we were never taught about poofs, rather we saw them and produced our own...
  37. K

    MHB Book Recommendations for Proofs

    I want a good book with an introduction to either graduate or undergraduate mathematics that has excercises and clear explanations.
  38. V

    An Intuitive Understanding Vs. Analytic Proofs

    Hey Physicsforums, This is something I run into quite a bit in my study of mathematics. Proofs are very important - that much is true. However, there are many instances when I don't need a proof to understand a concept; I just understand it. For example, I don't need...
  39. Government$

    Proving Inequalities: Three Exercises from Velleman's How to Prove It"

    I am doing exercises form Velleman's How to Prove It Homework Statement 1. Suppose a and b are real numbers. Prove that if a < b < 0 then a^2 > b^2. 2. Suppose a and b are real numbers. Prove that if 0 < a < b then 1/b < 1/a. 3. Suppose a and b are real numbers. Prove that if a < b...
  40. F

    Proofs in Algebra vs Proofs in Analysis

    Both algebra and analysis are pretty much all about proofs...but a prof told me the proofs in algebra are very different from those of analysis. How are they different? Any input appreciated.
  41. O

    Divisibility Proof: 9^n-5^n is Divisible by 4

    Can anyone help me confirm if I have solved this correctly? Many thanks. Homework Statement Q. 9^n-5^n is divisible by 4, for n\in\mathbb{N}_0 The Attempt at a Solution Step 1: For n=1... 9^1-5^1=4, which can be divided by 4. Therefore, n=1 is true... Step 2: For n=k...
  42. S

    Do I have to know all the euclidean elements proofs?

    Is it necessary to know the proofs of all the propositions in Euclid's elements? Or one can directly jump to euclidean and precollege geometry, of course he/she will have knowledge of propositions( just the statements and all that) but not the proofs. Reply Quickly.
  43. T

    Struggling with Proofs in Calculus/Analysis: Need Advice!

    I need some advice on proofs in my calculus/analysis course. I just wrote a test and it didn't go anywhere near according to plan. My problem keeps on revolving around how to do proofs of certain claims. Now the proofs for these claims on the test at least were proofs for the most part straight...
  44. B

    Books to Buy for Mathematical Maturity in Theory and Proofs

    I hope this is in the right section, otherwise please move it. This might be a long post and I hope someone will give it a shot. It is about books but not really a comparison between them. I will give some background first, so you might skip to the end (- Books * -) if you are only interested in...
  45. J

    Writing Computations Clearly In Proofs

    Here's a quick question concerning writing clearly in proofs. I am revising and refining some of my proofs [this is for a self-study], and I across a problem where I had to prove that f: G->G defined by f(x)=axa-1 is a automorphism. To show it has the homomorphism property, I had to do some...
  46. B

    Prove 1-n^2>0: 3n-2 is Even Integer

    Let nεZ,Prove that 1-n^2>0, then 3n-2 is an even integer. I proved it like this. I think its right but I am not able to word it correctly. Since 1-n^2>0 therefore n=0. Then 3n-6=3(0)-2=-2. Since 0 is an integer, 3n-6 is even. How can I learn to word this correctly because I am having some...
  47. B

    Prove 1-n^2>0, Then 3n-2 is Even | Math Homework Help

    Homework Statement Let nεZ,Prove that 1-n^2>0, then 3n-2 is an even integer. Homework Equations The Attempt at a Solution I proved it like this. I think its right but I am not able to word it correctly. Since 1-n^2>0 therefore n=0. Then 3n-6=3(0)-6=-6. Since 0 is an integer, 3n-6 is even...
  48. J

    Books recommendation for Mathematical proofs

    Hi, I was wondering if you can suggest good books on the techniques for mathematical proofs. I know this is quite a simple matter but I would be glad if you could suggest me with greats books for teaching proofs. More often than not I used the direct method and induction to prove problems in...
  49. B

    Reading Mathematical Theorems And Their Proofs

    Lately, I have been experiencing a sort of anxiety over not understanding some of these proofs in my calculus textbook. I just finished a calculus I course, and we did not spend any time learning them; so, I thought, since it is summer time now, I would go back over and try to learn those...
  50. K

    Algebraic proofs of trigonometric identities

    Hello all, I was wondering if someone has ever found a purely algebraic proof for the addition/subtraction theorems of trigonometry, mainly sin(a+b)=sin(a)cos(b)+sin(b)cos(a). Given a right triangle: Let x be one of the perpendicular legs and let the other leg be composed of two parts, y1...
Back
Top