Schwarzschild Definition and 319 Threads
-
H
Volume of a black hole using the Schwarzschild metric
Hi, I'm wondering if it is possible to calculate the volume of a black hole using the Schwarzschild metric. After computing the volume I get the follow integral: $$V = 4 \pi \int_0^r \frac{1}{\sqrt{ (1- \frac{r_s}{r'})}} r'^2 dr$$ This integral diverges at the upper bound. The only way I...- happyparticle
- Thread
- Black hole General relativity Schwarzschild
- Replies: 34
- Forum: Advanced Physics Homework Help
-
D
I Orbital Period In General Relativity
What is the orbital period in General Relativity using the Schwarzschild metric? In classical mechanics, it is something like T=2pi(GnM/a3). Where a is the semi-major axis, this is for a small body orbiting a larger one. I think I have an idea but I am not 100% sure. I am interested in an...- dsaun777
- Thread
- Metric Orbital Schwarzschild
- Replies: 3
- Forum: Special and General Relativity
-

A Dirac's coordinates ##(\tau, \rho)## for the Schwarzschild metric with ##r \le 2m##
Dirac in his "GTR" (Chap 19, page 34-35) finds a coordinate system ##(\tau, \rho)## which has no coordinate singularity at ##r=2m##. Explicitly, the transformation looks like (after some algebra): $$\tau=t + 4m\sqrt{\frac{r}{2m}} + 2m\log{\frac{\sqrt{r/2m}-1}{\sqrt{r/2m}+1}}$$ $$\rho=t +...- Kostik
- Thread
- Coordinates Dirac Schwarzschild
- Replies: 5
- Forum: Special and General Relativity
-

I What is the proper time of a vertically moving inertial clock?
Hi. I am looking for an equation for the round trip elapsed proper time of a clock that is initially moving vertically straight up with a given initial velocity, reaches apogee and then returns to the starting location under gravity. I would like to use the external Schwarzschild geometry of a...- KDP
- Thread
- Freefall Proper time Schwarzschild
- Replies: 4
- Forum: Special and General Relativity
-
J
I Schwarzschild Geometry: Einstein Tensor & Mass Density
The Einstein tensors for the Schwarzschild Geometry equal zero. Why do they not equal something that has to do with the central mass, given that the Einstein equations are of the form: Curvature Measure = Measure of Energy/Matter Density?- Joe Prendergast
- Thread
- Einstein equation Schwarzschild Schwarzschild geometry Tensor
- Replies: 18
- Forum: Special and General Relativity
-

Solution to Schwarzschild Equation for Constant t,r
In 1916, Karl Schwarzschild was the first person to present a solution to Einstein's field equations. I am using a form of his equation that is presented in Tensors, Relativity and Cosmology by Mirjana Dalarsson and Nils Dalarsson (Chapter 19, p.205). I am approaching what may be the simplest...- kirkr
- Thread
- Constant Integration Schwarzschild
- Replies: 10
- Forum: Advanced Physics Homework Help
-
E
I Circular Orbit in Schwarzschild: Orbital Period
Schutz finds that the orbital period for a circular orbit in Schwarzschild is $$ P = 2 \pi \sqrt {\frac { r^3} {M} }$$ He gets this from $$ \frac {dt} {d\phi} = \frac {dt / d\tau} {d\phi/d\tau} $$ Where previously he had ## \frac {d\phi}{d\tau} = \tilde L / r^2## and ## \frac {dt}{d\tau} =...- epovo
- Thread
- Circular Circular orbit Orbit Orbital Orbital period Period Schwarzschild
- Replies: 5
- Forum: Special and General Relativity
-
I How to obtain other inverse metrics than that of Schwarzschild?
The Schwarzschild solution could simply be expressed as $$ds^2=-(1-2GM/r)dt^2+(1-2GM/r)^-1dr^2+r^2d\omega^2$$. Is it possible that we could obtained a new metric into the form as $$ds^2=-(1-2GM/r)^-1dt^2+(1-2GM/r)dr^2+r^2d\omega^2$$? If possible, what are the steps and procedures that should be...- Bishal Banjara
- Thread
- Inverse Schwarzschild
- Replies: 50
- Forum: Special and General Relativity
-
E
I Schwarzschild in Cartesian: Tricks for Transformation
According to Schutz, the line element for large r in Schwarzschild is $$ ds^2 \approx - ( 1 - \frac {2M} {r}) dt^2 + (1 + \frac {2M} {r}) dr^2 + r^2 d\Omega^2 $$ and one can find coordinates (x, y, z) such that this becomes $$ ds^2 \approx - ( 1 - \frac {2M} {R}) dt^2 + (1 + \frac {2M} {R})...- epovo
- Thread
- Cartesian Schwarzschild
- Replies: 18
- Forum: Special and General Relativity
-

Schwarzschild radius of the Universe
https://www.msn.com/en-us/news/technology/the-astonishing-scientific-theory-that-says-the-universe-might-be-inside-a-black-hole/ar-AA17lxtF?ocid=msedgdhp&pc=U531&cvid=272cb184de9c48fbbd3b321120e37dac Michio Kaku has often joked, "If you want to know what it looks like inside of a black hole...- Ivan Seeking
- Thread
- Radius Schwarzschild Schwarzschild radius Universe
- Replies: 30
- Forum: Cosmology
-

I Karl Schwarzschild: Solving GR on the Eastern Front
Read the bio / fiction chapter on Karl Schwarzschild in Benjamin Labatut’s great Book, and curious on a little color on how he developed the solution - I had thought finding an exact solution in GR was just math chops, but actually any Lorentzian metric is an exact solution, so the difficulty...- BWV
- Thread
- Gr Schwarzschild
- Replies: 4
- Forum: Special and General Relativity
-

A Connectedness of Boundary Points in Schwarzschild Penrose Chart
In the Penrose chart for Schwarzschild spacetime, the boundary "at infinity" appears to be connected all the way around. I want to explore what that means physically and whether particular boundary points that appear to be connected on the chart actually are. I am using the following notes as a...- PeterDonis
- Thread
- Boundary Penrose Points Schwarzschild
- Replies: 7
- Forum: Special and General Relativity
-

A Schwarzschild Geometry: Evaluating Proper Distance
Schwarzschild Geometry-proper distance. From what I have studied when the Schwarzschild line element is evaluated at constant time and at a constant radius , proper distance becomes a Euclidean distance on the surface of a sphere. What I don't understand is how to evaluate the integral...- kirkr
- Thread
- General relativity Geometry Proper distance Schwarzschild Schwarzschild geometry
- Replies: 9
- Forum: Special and General Relativity
-
A
I Schwarzschild Metric & Particle Absorption
The Schwarzschild metric implies a potential different from that of Newtonian gravity. Is there a relationship between it and the process by which particles can be absorbed by other particles? (I haven't studied QFT yet)- accdd
- Thread
- Absorption Metric Particle Schwarzschild Schwarzschild metric
- Replies: 8
- Forum: Special and General Relativity
-
A
I Differences b/w Schwarzschild Radius & Event Horizon
I understood that the event horizon is a null surface and not a place in space, what is the relationship between it and the Schwarzschild radius? Also, what does the Schwarzschild radius physically represent for example for an object such as a star?- accdd
- Thread
- Event horizon Horizon Radius Schwarzschild Schwarzschild radius
- Replies: 11
- Forum: Special and General Relativity
-

I Adapting Schwarzschild Metric for Nonzero Λ
So, there are a fair amount of metrics designed with a zero value for the cosmological constant in mind. I was wondering if there was some method to modify metrics to account for a nonzero cosmological constant. Say, for instance, the Schwarzschild metric due to its relative simplicity. A...- Sciencemaster
- Thread
- Cosmological constant Einstein field equations General relativity Metric Schwarzchild metric Schwarzschild Schwarzschild metric
- Replies: 4
- Forum: Special and General Relativity
-
A
I Schwarzschild Radius vs Event Horizon: Black Hole?
Real quick, are the terms "Schwarzschild Radius" and "Event Horizon" for a black hole interchangeable or is there some subtle difference between the two? Just looking for a ballpark answer here- Albertgauss
- Thread
- Difference Horizon Schwarzschild
- Replies: 30
- Forum: Special and General Relativity
-

I Coord. Time Vector Field: Schwarzschild vs Gullstrand-Painleve
Hi, I was reading this insight schwarzschild-geometry-part-1 about the transformation employed to rescale the Schwarzschild coordinate time ##t## to reflect the proper time ##T## of radially infalling objects (Gullstrand-Painleve coordinate time ##T##). As far as I understand it, the vector...- cianfa72
- Thread
- Coordinate Coordinate chart Field Schwarzschild Schwarzschild geometry Spacetime curvature Spacetime metric Time Vector Vector field
- Replies: 16
- Forum: Special and General Relativity
-
C
Space-like trajectory in Schwarzschild spacetime
I'm not sure how to approach this question. So I start off with the fact the path taken is space-like, $$ds^2>0$$ Input the Schwarzschild metric, $$−(1−\frac{2GM}{r})dt^2+(1−\frac{2GM}{r})^{−1}dr^2>0$$ Where I assume the mass doesn't move in angular direction. How should I continue?- crime9894
- Thread
- Black hole General relativity Schwarzchild metric Schwarzschild Spacetime Trajectory
- Replies: 3
- Forum: Advanced Physics Homework Help
-

Insights Geodesic Congruences in FRW, Schwarzschild and Kerr Spacetimes
Continue reading...- ergospherical
- Thread
- Geodesic Kerr Schwarzschild
- Replies: 8
- Forum: Special and General Relativity
-

I Geodesics in Schwarzschild metric
Hello, there. I am learning the chapter, The Schwarzschild Solution, in Spacetime and geometry by Caroll. I could not grasp the idea of circular orbits. It starts from the equations for ##r##, $$\frac 1 2 (\frac {dr}{d \lambda})^2 +V(r) =\mathcal E$$ where $$V(r)=\frac {L^2}{2r^2}-\frac...- Haorong Wu
- Thread
- Geodesics Metric Schwarzschild Schwarzschild metric
- Replies: 42
- Forum: Special and General Relativity
-

I Schwarzschild Metric Singularity: Why?
Why does the Schwarzschild metric have a singularity at r=0 if it is only valid outside the spherically symmetric static mass?- Charles_Xu
- Thread
- Metric Schwarzschild Schwarzschild metric Singularity
- Replies: 4
- Forum: Special and General Relativity
-

I Gravity at Schwarzschild Radius of a Black Hole
From "standard" formula we have that the gravity acceleration a = GM/r^2 and that the Schwarzschild radius rs = 2 GM / c^2 Is it possible to compute the gravity acceleration at Schwarzschild radius putting r = rs? In this case we will have a = c^4 / (4GM) This mean that a very very...- Roberto Pavani
- Thread
- Black hole Black holes General relativity Hole Schwarzschild Ship Space
- Replies: 17
- Forum: Special and General Relativity
-

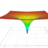
I Discussing Interior Schwarzschild Proper Lengths & Gaussian Curvature
I'd love have a little discussion about the Interior Schwarzschild Solution. Here's a diagram I slapped together to illustrate the key points. (I assume everyone reading this familiar with embedding diagrams, and using an axis to 'project' a value, in this case the spatial z-axis is replaced by...- D.S.Beyer
- Thread
- Curvature Gaussian Interior Schwarzschild Schwarzschild solution Visualization
- Replies: 2
- Forum: Special and General Relativity
-

A Computing Null Geodesics in Schwarzschild Geometry
Computing timelike geodesics in the Schwarzschild geometry is pretty straightforward using conserved quantities. You can treat the problem as a variational problem with an effective Lagrangian of ##\mathcal{L} = \frac{1}{2} (Q \frac{dt}{d\tau}^2 - \frac{1}{Q} \frac{dr}{d\tau}^2 - r^2...- stevendaryl
- Thread
- Computing Geodesics Geometry Null geodesics Schwarzschild Schwarzschild geometry
- Replies: 4
- Forum: Special and General Relativity
-

Python Python Packages to Calculate orbits in Schwarzschild Metric
I am looking for a Python Code/Package to calculate the orbits of the time-like and null-like particles in Schwarzschild metric (in spherical coordinates) Does anyone know such package ? Note: I am mostly looking for packages to calculate the RIGHT side of the given images (i.e the orbits...- Arman777
- Thread
- Metric Orbits Python Schwarzschild Schwarzschild metric
- Replies: 6
- Forum: Programming and Computer Science
-

Wave equation for Schwarzschild metric
I am trying to find the $$\nabla_{\mu}\nabla^{\mu} \Phi$$ for $$ds^2 = (1 - \frac{2M}{r})dt^2 + (1 - \frac{2M}{r})^{-1}dr^2 + r^2d\Omega^2$$ I have did some calculations by using $$\nabla_{\mu}\nabla^{\mu}\Phi = \frac{1}{\sqrt{-g}}\partial_{\mu}(\sqrt{-g}g^{\mu \nu}\partial_{\nu}\Phi)$$...- Arman777
- Thread
- Metric Schwarzschild Schwarzschild metric Wave Wave equation
- Replies: 4
- Forum: Advanced Physics Homework Help
-
V
I Klein-Gordon: Schwarzschild Metric, Physically Acceptable?
Does this give solutions which are physically acceptable?- Vitani1
- Thread
- Klein-gordon Metric Schwarzschild Schwarzschild metric
- Replies: 7
- Forum: Special and General Relativity
-

I Inverting the metric coefficients in the Schwarzschild line element
Assuming the line element ##ds^s=e^{2\alpha}dt^2-e^{2\beta}dr^2-r^2{d\Omega}^2 ##as usual into the form ##ds^s=e^{-2\alpha}dt^2-e^{-2\beta}dr^2-r^2{d\Omega}^2##, I found that the ##G_{tt}## tensor component of first expression do not reconcile with the second one though, it fits for ##G_{rr}...- Bishal Banjara
- Thread
- Coefficients Element Line Line element Metric Schwarzschild
- Replies: 32
- Forum: Special and General Relativity
-

I Interpreting Schwarzschild Metric: Photon Falls Toward Black Hole
As a photon falls radially toward the surface of a Schwarzschild black hole, dr/dt approaches zero. Does this mean that, from the viewpoint of a distant (Schwarzschild) observer, the photon slows down or that the distance covered by successive dr's is getting larger?- snoopies622
- Thread
- Metric Schwarzschild Schwarzschild metric
- Replies: 18
- Forum: Special and General Relativity
-
O
What Are the Values of \(a\) and \(b\) in the Schwarzschild 4-Velocity?
So the line element is given by $$ ds^2 = (1- \frac{R_s}{r})dt^2 - (1- \frac{R_s}{r})^{-1}dr^2 - r^2d\Omega ^2$$ The object is orbiting at constant radius ##r## in the plane ## \theta = \frac{\pi}{2}##. I am supposed to find the values of ##a## and ##b## in the 4-velocity given by: $$U =...- Omikron123
- Thread
- 4-vector Schwarzchild Schwarzchild metric Schwarzschild
- Replies: 10
- Forum: Advanced Physics Homework Help
-

A GR: Is Schwarzschild Spacetime Time-Independent?
I'm a bit confused about GR : what is more significant about the considered spacetime, the metric, which is time-independent, or the embedding (there are already some posts on PF about it), which describes the shape of a manifold, but is time-dependent ?- jk22
- Thread
- Schwarzschild Spacetime Time-independent
- Replies: 3
- Forum: Special and General Relativity
-
D
I The Schwarzschild Radius: Mass vs. Energy
When calculating the Schwarzschild radius are we supposed to be using the rest mass of the object or its total energy?- dsaun777
- Thread
- Radius Schwarzschild Schwarzschild radius
- Replies: 15
- Forum: Special and General Relativity
-
P
I Energy in the Schwarzschild spacetime
I had a thought that I wanted to share in another thread, but it wandered way off track and quite properly was closed. But I thought the separate idea that I had spawned from the old thread was worthy of posting in a new thread. I do not want to re-open the old thread, though! In flat...- pervect
- Thread
- Energy Schwarzschild Spacetime
- Replies: 30
- Forum: Special and General Relativity
-

B What Happens to Time on a Clock at r=r_{s}/2 Inside a Schwarzschild Black Hole?
I notice that in a Schwarzschild black hole, at r=r_{s}/2, the c dt and dr terms are exactly the opposite of what they are in external, normal flat space (Minkowski metric). That is, one gets them by multiplying both terms by negative one. I'm having trouble grasping what this means. An...- snoopies622
- Thread
- Black hole Hole Schwarzschild Time
- Replies: 11
- Forum: Special and General Relativity
-
U
I Calculating Surface Area of Schwarzschild Black Hole w/Weyl Coordinates
Recently, I was tasked to find the surface area of the Schwarzschild Black Hole. I have managed to do so using spherical and prolate spheroidal coordinates. However, my lecturer insists on only using Weyl canonical coordinates to directly calculate the surface area. The apparent problem arises...- user1139
- Thread
- Area Black hole Coordinates Hole Schwarzschild Surface Surface area Weyl
- Replies: 15
- Forum: Special and General Relativity
-
T
A poor man's way to Schwarzschild Geometry
Can anyone help me get started with this problem? What should I use for Gni? I've tried to produce Tni by working out Rni (using methods developed in an earlier chapter) but the results don't lead me anywhere. I'm really stuck for a way forward on this problem so if anyone can help, it...- TerryW
- Thread
- Geometry Schwarzschild Schwarzschild geometry
- Replies: 25
- Forum: Advanced Physics Homework Help
-

I The proper Schwarzschild radial distance between two spherical shells
For the purpose of this thread the metric is ds2 = - (1-rs/r) c2 dt2 + dr2 / (1-rs/r) where rs = 2GM/c2. (I modified the above from https://jila.colorado.edu/~ajsh/bh/schwp.html .) I assume that the two spherical shells are stationary. Therefore dt = 0. The r coordinate for the radii of the...- Buzz Bloom
- Thread
- Radial Schwarzschild Spherical
- Replies: 45
- Forum: Special and General Relativity
-
K
I Study After Schwarzschild Spacetime: What's Next?
For someone who have just finished the study of the (fundamentals) of Schwarzschild spacetime, what would be the next natural topic to study?- kent davidge
- Thread
- Schwarzschild Spacetime Study
- Replies: 14
- Forum: Special and General Relativity
-

I Solving Confusion About Black Holes, Schwarzschild Radius & Time Dilation
According to the theory, every mass has a Schwarzschild radius associated. Any object whose radius is smaller than its Schwarzschild radius is called a black hole. So in principle is possible to create mini-black holes, it is just a fact of matter condensed. Those mini black holes have their...- arkantos
- Thread
- Confusion Dilation Radius Schwarzschild Schwarzschild radius Time Time dilation
- Replies: 3
- Forum: Special and General Relativity
-
G
I Strongest Evidence for Trapping Light in Schwarzschild Radius
The concept of that when a photon's trajectory intersects with the Schwarzschild Radius/event horizon, said photon will never exit the Schwarzschild Radius/event horizon. Or any other object besides a photon for that matter. So far what has been the strongest evidence for this prediction?- greswd
- Thread
- Evidence Light Radius Schwarzschild Schwarzschild radius
- Replies: 6
- Forum: Special and General Relativity
-
S
Schwarzschild coordinate time integral
I have tried integration by parts where, ##c dt = -\frac{1}{\sqrt{r*}} \frac{r^{3/2} dr}{r - r*} = \frac{1}{\sqrt{(r*)^3}} \frac{r^{3/2} dr}{1 - \Big(\sqrt{\frac{r}{r*}} \Big)^2}## ##u = r^{3/2} \quad \quad dv = \frac{dr}{1 - \Big(\sqrt{\frac{r}{r*}} \Big)^2}## ##du = \frac{3}{2} r^{1/2} dr...- shinobi20
- Thread
- Calculus Coordinate General relaivity Integral Schwarzchild metric Schwarzschild Time
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
E
A Schwarzschild Metric Geodesic Eq: Qs & Answers
I have no idea if this is an “A” level question, but I will put that down. From the Schwarzschild metric, and with the help of the Maxima program, one of the geodesic equations is: (I will have to attach a pdf for the equations...) I believe this integrates to the following, with ...- exmarine
- Thread
- Geodesic Metric Schwarzschild Schwarzschild metric
- Replies: 15
- Forum: Special and General Relativity
-

I with an exercise about Energy and Schwarzschild Black Holes
The thing is that this is an exercise that I have to show my teacher but I don´t know how to get the answer.The exercise says: "A body of mass m moving in the Keplerian field V = −M/r (in G = 1 units) has a total conserved energy, Etot = 1 /2( m r˙^2 + r ^2ϕ˙ ^2 )− mM/r. Show that the...- JTorn
- Thread
- Black holes Energy Exercise Holes Schwarzschild
- Replies: 8
- Forum: Advanced Physics Homework Help
-
P
I Active Diffeomorphisms of Schwarzschild Metric
I am trying to understand active diffeomorphism by looking at Schwarzschild metric as an example. Consider the Schwarzschild metric given by the metric $$g(r,t) = (1-\frac{r_s}{r}) dt^2 - \frac{1}{(1-\frac{r_s}{r})} dr^2 - r^2 d\Omega^2 $$ We identify the metric new metric at r with the old...- Prathyush
- Thread
- Diffeomorphisms Metric Schwarzschild Schwarzschild metric
- Replies: 6
- Forum: Special and General Relativity
-

B Schwarzschild radius of an object is smaller than Planck length
I had this idea when some people said that LHC can produce black hole. Based on the calculation of Schwarzschild Radius, any mass than 9.375×10^7 kg have a Schwarzschild radius smaller than the plank length. Particles inside LHC or other particle accelerator have clearly radii smaller than that...- ColdheartedGod
- Thread
- Length Lhc Planck Planck length Radius Schwarzschild Schwarzschild radius
- Replies: 3
- Forum: Other Physics Topics
-
P
I Coordinate time between spatially separated events in Schwarzschild spacetime
Edit: I'm leaving the original post as is, but after discussion I'm not confused over coordinate time having a physical meaning. I was confused over a particular use of a coordinate time difference to solve a problem, in which a particular coordinate time interval for a particular choice of...- physlosopher
- Thread
- Coordinate Events Schwarzschild Spacetime Time
- Replies: 58
- Forum: Special and General Relativity
-
S
I The Singularity and the Schwarzschild radius
A singularity would be: a location in spacetime where the gravitational field of a celestial body is predicted to become infinite by general relativity in a way that does not depend on the coordinate system. (wiki) If the threshold to get a singularity is reached then space-time curvature...- stg213
- Thread
- Radius Schwarzschild Schwarzschild radius Singularity
- Replies: 25
- Forum: Special and General Relativity
-
K
I Radius in Schwarzschild Metric: Definition Explained
Hello! I am a bit confused about the definition of the radius in Schwarzschild metric. In the Schutz book on GR (pg. 264, General rules for integrating the equations) he says: "A tiny sphere of radius ##r = \epsilon## has circumference ##2\pi\epsilon##, and proper radius...- kelly0303
- Thread
- Metric Radius Schwarzschild Schwarzschild metric
- Replies: 7
- Forum: Special and General Relativity
-

I Schwarzschild Geodesics: An Overview
- Goldman clarck
- Thread
- Black hole General relativity Geodesics Schwarzschild
- Replies: 7
- Forum: Special and General Relativity