Second order ode Definition and 91 Threads

In mathematics, a differential equation is an equation that relates one or more functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology.
Mainly the study of differential equations consists of the study of their solutions (the set of functions that satisfy each equation), and of the properties of their solutions. Only the simplest differential equations are solvable by explicit formulas; however, many properties of solutions of a given differential equation may be determined without computing them exactly.
Often when a closed-form expression for the solutions is not available, solutions may be approximated numerically using computers. The theory of dynamical systems puts emphasis on qualitative analysis of systems described by differential equations, while many numerical methods have been developed to determine solutions with a given degree of accuracy.

View More On Wikipedia.org
Recent contents Top users
  1. Safinaz

    How to Approach Solving a Nonlinear Second Order ODE with a Quadratic Term?

    I know how to solve similar ODEs like ## \frac{\partial^2 x}{ \partial t^2} + b \frac{\partial x}{ \partial t} + C x =0 ## Where one can let ## x = e^{rt}##, and the equation becomes ## r^2 + b r + C =0 ## Which can be solved as a quadratic equation. But now the problem is that there is...
  2. G

    [Sturm-Liouville eigenvalues and eigenfunctions problem]

    I have found that w(x) should be e^-x to make L self-adjoint. and insert back get xL''+(x+1)L' +lambda L = 0 now it needs to assume a monic polynomial function, so I assume Ln = x^n+ sum from k=0 to n-1 (a_k*x^k) get the 1st and 2nd order differential and insert back I get lambda_n =...
  3. H

    I Second order non-homogeneous linear ordinary differential equation

    I shall not begin with expressing my annoyance at the perfect equality between the number of people studying ODE and the numbers of ways of solving the Second Order Non-homogeneous Linear Ordinary Differential Equation (I'm a little doubtful about the correct syntactical position of 'linear')...
  4. T

    I Second Order ODE with Exponential Coefficients

    Hi all, I have another second order ODE that I need help with simplifying/solving: ##p''(x) - D\frac{e^{\gamma x}}{A-Ae^{\gamma x}}p'(x) - Fp(x) = 0## where ##\gamma,A,F## can all be assumed to be nonzero real numbers and ##D## is a purely nonzero imaginary number. Any help would be appreciated!
  5. T

    I Converting Second Order ODE to Hypergeometric Function

    I believe it is the case that any linear second order ode with at most 3 regular singular points can be transformed into a hypergeometric function. I am trying to solve the following equation for a(x): where E, m, v, k_{y} are all constants and I believe turning it into hypergeometric form will...
  6. I

    ODE solver for second Order ODE with Stiffness and Mass Matrices

    i am new to MATLAB and and as shown below I have a second order differential equation M*u''+K*u=F(t) where M is the mass matrix and K is the stifness matrix and u is the displacement. and i have to write a code for MATLAB using ODE45 to get a solution for u. there was not so much information on...
  7. jisbon

    Engineering Heun's Method for Second Order ODE (Eng Maths)

    Question: So I got around on doing this example, and I'm pretty sure I messed up somewhere, would appreciate if someone could point out what I did wrongly. 1) For any second ODE, I should let: ##y_{1}= y ## and ##y_{2}= y' ## Hence, ##y_{1}'= y' = y_{2} ## and ##y_{2}'= y'' = xy(x)+x^2-y(x) =...
  8. agnimusayoti

    Another Second Order ODE Problem (ML Boas, Ch 8, Sec 7, Prob 5)

    With the new variable, I got: $$p^2 (p'_y)^{2}=k^2(1+p^2)$$ where ##p'_y## is ##\frac{dp}{dy}##. I modified the equation so the variable p and dp can be separated from dy. Here what I got: $$\frac{p}{\sqrt{p^2+1}} dp=k dy$$ I substitute ##p^2+1=u## so I got $$\sqrt{u}=ky+c_1$$ Back substitution...
  9. chwala

    Understanding the Frobenius Method for Solving Second Order ODEs

    let ##y= \sum_{k=-∞}^\infty a_kz^{k+c}## ##y'=\sum_{k=-∞}^\infty (k+c)a_kz^{k+c-1}## ##y"=\sum_{k=-∞}^\infty (k+c)(k+c-1)a_kz^{k+c-2}## therefore, ##y"+y'\frac {1}{z}+y[\frac {z^2-n^2}{z^2}]=0## =##[\sum_{k=-∞}^\infty [(k+c)^2-n^2)]a_k + a_k-2]z^{k+c} ## it follows that...
  10. T

    I Nonlinear Second Order ODE: Can We Find an Analytical Solution?

    I'm trying to solve the following nonlinear second order ODE where ##a## and ##b## are constants: $$\frac{d^2y}{dx^2}+\frac{1}{x}\frac{dy}{dx}-\frac{y}{ay+b}=0$$ It looks somewhat like the modified Bessel equation, except the third term on the left makes it nonlinear. I've been trying to...
  11. T

    I Solution to a second order differential equation

    I have currently been reading a book called 'Mathematical Methods In Physical Sciences'. Whilest I was looking at the differential section I came across a differential which I have never thought about before, which is of the form...
  12. B

    Variation of Parameters to solve a second order ODE

    Homework Statement The question I am working on is the one in the file attached. Homework Equations y = u1y1 + u2y2 : u1'y1 + u2'y2 = 0 u1'y1' + u2'y2' = g(t) The Attempt at a Solution I think I have got part (i) completed, with y1 = e3it and y2 = e-3it. This gives a general solution to the...
  13. B

    Solving a second order ODE using reduction of order

    Homework Statement Hi there, I have an assignment which involves using reduction of order to solve for a second solution to an ode (the one attached). However this is a method I am new to, and though I have tried several times, I'm somehow getting something wrong because the LHS and RHS are not...
  14. K

    Second order ODE: finding solution.

    Homework Statement d2u/d2x + 1/2Lu = 0 where L is function of x Homework Equations I am try to find solutions y1 and y2 of this equation. The Attempt at a Solution y = [cos √(L/2) x] + [sin √(L/2) x] y' = - [√(L/2) sin √(L/2) x] + [ √(L/2) cos √(L/2) x] y'' = -[(L/2) cos √(L/2) x] -...
  15. F

    I Second order DE with Sine function

    I have this second order differential equation but I'm stumped as to how to solve this since the zeroth order term has a Sine function in it and the variable is embedded. ##\ddot y(t) + 3H (1+Q) \dot y(t) -m^2 f \sin(\frac{y(t)}{f}) = 0## ##H~##, ##~Q~##, ##~m~##, and ##~f~## are just...
  16. B

    Convert second order of diff. equations to first order

    Homework Statement I have this set of equation: My''+Cy'+Ky=0 but C=0 M is a matrix consist of {(-m) (0)/( -1/12mb^2) (-1/12mb^3)} and K is a matrix of {(-K1-K2) (-K2b)/ ((K1b-K2b)/(2)) (-K2b^2/2)} and y is a coordinate system which is (x1,θ) Now i have to convert these...
  17. whatisgoingon

    Second order ODE into a system of first order ODEs

    Homework Statement The harmonic oscillator's equation of motion is: x'' + 2βx' + ω02x = f with the forcing of the form f(t) = f0sin(ωt)The Attempt at a Solution So I got: X1 = x X1' = x' = X2 X2 = x' X2' = x'' ∴ X2' = -2βX2 - ω02X1 + sin(ωt) The function f(t) is making me doubt this answer...
  18. Cocoleia

    Second order non homogeneous ODE, IVP

    Homework Statement I need to solve: x^2y''-4xy'+6y=x^3, x>0, y(1)=3, y'(1)=9 Homework EquationsThe Attempt at a Solution I know that the answer is: y=x^2+2x^3+x^3lnx Where did I go wrong. I was wondering if it's even logical to solve it as an Euler Cauchy and then use variation of parameters...
  19. E

    I Can you check the solution for this second order ODE?

    The second order ODE is, \begin{equation*} \frac{d^2 x}{dt^2} = -\omega^2_g \frac{dx}{dt} \end{equation*} I tried solving this by substitution of the second order derivative into a variable and transforming the equation into a second order polynomial, and I get the solution involving an...
  20. G

    MHB Solving Second Order ODE: True or False?

    I'm supposed determine whether following statements are true or false. However, I can't get past the notation. Question: the second order differential equation $\ddot{x}+\dot{x}+x = 9t$ is: (a) equivalent to $\begin{cases} \dot{x} = y, & \\ \dot{y}=-y-x+9t, &\end{cases}$ (b) solved by...
  21. C

    Non-linear non-constant coefficient second order ODE

    I would like to solve the steady-state one dimensional heat equation for a two piece material system. The thermal conductivity in each segment is a linear function of temperature, where ##\kappa_1=a_1T+b_1## for material 1 and ##\kappa_2=a_2T+b_2## for material 2. ##a_1, a_2, b_1, and \;b_2##...
  22. Mark Brewer

    Finding a Second Linearly Independent Solution Using Reduction of Order

    Homework Statement (Reduction of order) The function y1 = x-1/2cosx is one solution to the differential equation x2y" + xy' + (x2 - 1/4) = 0. Use the method of reduction of order to find another linearly independent solution. The Attempt at a Solution I divided x2 to both sides to get the...
  23. W

    Construct a second order ODE given the solutions?

    Homework Statement I've been stuck on this problem for three days now, and I have no clue how to solve it. Construct a linear differential equation of order 2, for which { y_1(x) = sin(x), y_2(x) = xsin(x)} is a set of fundamental solutions on I = (0,\pi) . Homework Equations Wronskian for...
  24. Remixex

    Hooke's and Newton's law to find Second order ODE

    Homework Statement A weight of 8 pounds extends a spring 2 feet. It's assumed that the damping force that acts on the system is equal (number-wise) to alpha times the speed of the weight. Determine the value of alpha > zero so x(t) is critically damped. Determine x(t) if the weight is liberated...
  25. I

    Laplace Transform of A Second Order ODE

    23.) y'' + 2y' + y = 4e-t; y(0) = 2, y'(0) = -1 Y(s) = [(as + b) y(0) + a y'(0) + F(s)]/(as2 + bs + c) My attempt: a = 1, b = 2, c = 1 F(s) = 4 L{ e-t } = 4/(s+1) (From Laplace Transform Table) Plugging and simplifying: Y(s) = (2s2 + 5s + 7)/[(s + 1)(s2 + 2s + 1) Here is where I get...
  26. manifold

    A numerical solution of a second order ODE

    Hello everyone; i'd like some help in this problem : i want to solve num this differential equation { y"(t)+t*cos(y)=y } by the Taylor method second order expansion. i first have to make this a first order differential equation by taking this vector Z=[y' y] then we have Z'=[y" y'] which equal...
  27. F

    MHB Finding interval where second order ODE has unique solution

    I'm a little stuck getting started on this question. y''+\tan(x)y=e^x with y(0)=1,y'(0)=0. I know the existence and uniqueness theorem for an nth order initial value problem How do I apply the theorem?
  28. S

    General solution of second order ODE

    Homework Statement Find the general solution. Homework Equations y"+y=x2sin2x The Attempt at a Solution Characteristic equation would be: m2 + 1 = 0 So,m2 = -1 Therefore, m = i or m = -i. Complementary function would be : Asinx+Bcosx where,A and B are constants respectively. If I write...
  29. icesalmon

    Second order ODE for RLC circuit

    if I consider a circuit consisting of a capacitor, an inductor and a resistor and using kirchhoffs voltage rule for the circuit i come up with the following L(Q''(t)) + R(Q'(t)) + (Q(t))/C = 0 I solve for the roots using a characteristic equation of the form LM2 +MR +(1/C) = 0 solving this for...
  30. C

    How Can We Solve this Second Order ODE for Electron Behavior?

    Homework Statement I'm taking an online introductory chem course, and while explaing the failure of classical mechanics to describe electron behavior, the teacher brought up the following ode which is based on Newton's second law and coulombs law: -e^2/4(pi)(epsilon-nuaght)r^2=m(d^2r/dt^2)...
  31. C

    Oddly Formatted Second Order ODE

    Homework Statement u'' + w20*u = cos(wt) w refers to omega. Homework EquationsThe Attempt at a Solution I'm not sure where to begin on this. For starters, it's a multiple choice problem, and all the answers are given in terms of y, so I'm not sure if u is supposed to replace y' or something...
  32. _N3WTON_

    Second Order ODE, Complex Roots, Change of Variables

    Homework Statement Solve: \frac{d^{2}y}{dx^{2}} + \omega^{2}y = 0 Show that the general solution can be written in the form: y(x) = A\sin(\omega x + \alpha) Where A and alpha are arbitrary constants Homework EquationsThe Attempt at a Solution I know that I will need to change variables for...
  33. C

    Second Order ODE, With Initial Conditions

    Homework Statement y'' + 4y = t2 + 6et; y(0) = 0; y'(0) = 5 Homework Equations The Attempt at a Solution So, getting the general solution, we have r2 + 4 = 0, so r = +/- 2i So the general solution is yc = sin(2t) + cos(2t) I then used the method of undetermined coefficients to figure that...
  34. MarkFL

    MHB Solve Linear Inhomogeneous 2nd Order ODE - Alvin's Question on Yahoo Answers

    Here is the question: I have posted a link there to this thread so the OP can view my work.
  35. T

    Laplace Transform Solution to Second Order ODE IVP

    Homework Statement y''+6y=f(t), y(0)=0, y'(0)=-2 f(t)= t for 0≤t<1 and 0 for t≥1 Homework Equations The Attempt at a Solution L{y''}+6L{y}=L{t}-L{tμ(t-1)} where μ(t-1) is Unit Step Y(s)=L{y} sY(s)-y(0)=L{y'} and y(0)=0 s2Y(s)-sy(0)-y'(0)+6Y(s) where y(0)=0 and...
  36. F

    Mass on a spring non-homogeneous second order ODE

    Homework Statement A mass of 5kg stretches a spring 10cm. The mass is acted upon by an external force of 10sin(t/2) Newtons and moves in a medium that imparts a viscous force of 2N when the speed of the mass is 4cm/sec. If the mass is set in motion from its equilibrium position with an initial...
  37. T

    Solve second order ode with Green function

    I had made a post in the past about the same problem and unfortunately I wasn't clear enough so I am trying again. I am studying an article and there I found without any proof that the solution of: Let ##g \in \mathbb{C}## and let ##u:(0,\infty)\to \mathbb{C}## $$ -u''+\lambda^2u=f\,\, on...
  38. T

    Solve second order ode with Green's functions

    -u''(z)+α2u(z)=f(z), u(0)=g(z), u(z)=0 as z→∞ -u''(z)+α2u'(z)=f(z), u(0)=g(z), u(z)=0 as z→∞ I am interested to solve these two boundary problems using Green's functions. It is noticed that z is complex variable. Can someone help me to do this?
  39. E

    Can Fourier Series Simplify Solving Nonlinear ODEs with Oscillatory Inputs?

    Hi all, I have a nonlinear ODE in the following form: a x'' + b |x'|x' + c x' + d x = y where x and y are functions of time and a,b,c and d are constants. As far as I can tell the only way to solve this is numerically, something I've managed to do successfully using a Rung-Kutta scheme...
  40. D

    How Do You Solve a Second Order ODE with Specific Boundary Conditions?

    Homework Statement basically solve \frac{d^{2}y}{dx^{2}} + 4\frac{dy}{dx} + 4y = cos2x Boundary conditions are y=0, dy/dx =1 at x=0 Homework Equations The Attempt at a Solution I am having trouble getting the coefficients to the solution. I got the complementary function as...
  41. fluidistic

    Variation of parameters for a second order ODE

    Homework Statement I must solve ##y''+2y'+2y=e^{-t}\sin t##. I know variation of parameters might not be the fastest/better way to solve this problem but I wanted to practice it as I never, ever, could solve a DE with it. (Still can't with this one). Though the method is supposed to work...
  42. fluidistic

    Second order ODE, I think 2 regular points

    Homework Statement Hello guys! I've never dealt with an ODE having 2 singularities at once, I tried to solve it but ran out of ideas. I must solve ##(x-2)y''+3y'+4\frac{y}{x^2}=0##. Homework Equations Not sure. The Attempt at a Solution I rewrote the ODE into the form...
  43. C

    Second order ODE with RHS = product of two functions

    Homework Statement Find the general solution of the ODE $$ y'' + 16y = 64x \cos x.$$ If ## y(0)=1, y'(0) = 0##, what is the particular solution? The Attempt at a Solution I am confident I can tackle this question, I really just want to check that my particular integral form is correct. I...
  44. T

    Nonlinear second order ODE describing a force field

    Not sure if this topic belongs here, but here goes. Homework Statement From the AP physics C 1995 test there is a problem that gives the potential energy curve U(x). With F=-\frac{dU}{dx} in one variable, F(x)=-\frac{a}{b}+\frac{ba}{x^{2}} Where a and b are constants. Now I need to get...
  45. D

    Removing a Singularity for a Second Order ODE

    I was given the following equation to solve: x^2*y'' + x*y' + k^2*x^2*y = 0 B.C. y'(0)=0, y(1)=0 where k is just some constant. I am having a hard time removing the singularity created by the boundary condition at y' and not aware of a method how. Any advice would be greatly appreciated.
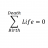
  46. STEMucator

    Proof of Second Order ODE Theorem

    Homework Statement I'm pretty sure this is a typo? http://gyazo.com/802746486cc68852e5384d5a12aed596 Homework Equations See the image ^. The Attempt at a Solution I believe the theorem they're talking about, is that you can write the general solution of a second order ODE : L[y] = y'' +...
  47. M

    Runge Kutta method to solve second order ODE

    Homework Statement Need to solve xy''+y'+xy=0 using Runge Kutta on x[1,3] Couldn't find algorythm to solve second order ODE using this method I know how to do 1st order Homework Equations The Attempt at a Solution I know I have to make this equation into 2 first order ODE...
  48. A

    Help solving a second order ODE with repeated roots,

    Help solving a second order ODE with repeated roots, urgent! I have a differential equaition d2y/dx2 - 6dy/dx + 9y = 0 I have found the general solution to be y = (Ax + B)e3x Now I need to find the solutions to A and B so that... when y = 4, x = 0 when y = 49.e15, x = 5 I...
  49. M

    Question about linear second order ODE solution coefficients

    Hey all, there is something that has always bugged me in linear second order ODEs. We say that the general solution is: y=C_1e^{r_1x}+C_2e^{r_2x} where r_1 and r_2 are the solutions of the characteristic polynomial. The cases where r1, r2 are real are pretty straightforward. If they are...
  50. S

    Solving 2nd Order ODE with x(0)=0, x'(0)=0

    I'm not sure exactly how to solve this ODE. (dx^2)/(dt^2) + (w^2)x = Fsinwt, where x(0) = 0 and X'(0) = 0. What I've got so far is: x'' + w^2x = Fsinwt --> x(homogenous) = Acoswt + Bsinwt I know I have to find a particular solution but I keep getting zero as a result which I know won't...
Back
Top