You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Space Definition and 1000 Threads
-
A
Conservation of Momentum Space Ship Problem
Homework Statement The payload of a spaceship accounts for 20% of its total mass. The ship is traveling in a straight line at 2100km/hr relative to some inertial observer O. When the time is right, the spaceship ejects the payload, which is moving away from the ship at 500km/hr immediately...- AnhTran
- Thread
- Replies: 4
- Forum: Introductory Physics Homework Help
-
D
I A surface integral over infinite space
Hi. If a function f is normalizable ,ie f→0 as | x | → infinity or r→ infinity then I presume the following surface integral f dS over infinite space is zero ? But I thought about this again and it seems like a case of zero x infinity. The function is zero at the infinite surface but the area... -
T
Do vacuum Ironing boards cause negative pressure in my Space
Hey, I'm designing an HVAC system for a laundry building. I have vacuum equipment (Vacuum press and Vacuum Ironing boards ) in the space which have a vacuum outlet the is taken outside the building through individual ducts. When all machines are operational, 877 l/s of hot air and moisture would... -
T
Forces - Space Shuttle Takeoff Calculations
Homework Statement [/B] The total mass of a space shuttle and its launch vehicle is M=2000t. a) What must be the minimum size of the thrust force, to make the rocket move? b) The actual thrust of the rocket is F=30MN. What is its acceleration in the beginning? c) Assume that a mass of a...- Taylan
- Thread
- Replies: 22
- Forum: Introductory Physics Homework Help
-
M
MHB The axioms of a vector space are satisfied
Hey! :o We consider the $\mathbb{F}_2$-vector space $(2^M, +, \cap)$, where $M$ is non-empty set and $+ : 2^M\times 2^M \rightarrow 2^M: (X,Y)\mapsto (X\cup Y)\setminus (X\cap Y)$. I want to show that $(2^M, +, \cap )$ for $\mathbb{K}=\{\emptyset , M\}$ satisfies the axioms of a vector space...- mathmari
- Thread
-
- Tags
- Axioms Space Vector Vector space
- Replies: 10
- Forum: Linear and Abstract Algebra
-
M
MHB Vector space - Prove or disprove
Hey! :o Let $1\leq n\in \mathbb{N}$ and let $U_1, U_2$ be subspaces of the $\mathbb{R}$-vector space $\mathbb{R}^n$. I want to prove or disprove the following: The set $\{f\in \mathbb{R}^{\mathbb{R}} \mid \exists x\in \mathbb{R} : f(x)=0_{\mathbb{R}}\}$ is a subspace of...- mathmari
- Thread
-
- Tags
- Space Vector Vector space
- Replies: 8
- Forum: Linear and Abstract Algebra
-

A Lorentz Invariant Phase Space: Symplectic Geometry
I have an assignment to show that specific intensity over frequency cubed \frac{I}{\nu^3}, is Lorentz invariant and one of the main topics there is to show that the phase space is Lorentz invariant. I did it by following J. Goodman paper, but my professor wants me to show this in another way...- gasar8
- Thread
- Replies: 1
- Forum: Special and General Relativity
-

A Representation of elements of the Grassmannian space
Hi, I am studying some material related to Grassmannians and in particular how to represent k-subspaces of ℝn as "points" in another space. I think understood the general idea behind the Plücker embedding, however, I recently came across another type of embedding (the "Projection embedding")...- mnb96
- Thread
-
- Tags
- Elements Representation Space
- Replies: 1
- Forum: Linear and Abstract Algebra
-

B What does it mean to say that "space" has a temperature?
I was thinking about the fact that space contains all sorts of matter and that these objects have temperatures. But then I read that space itself has a temperature depending on where you are. The cosmic background radiation for example has a temperature of 2.7K. Can someone explain what that...- Graeme M
- Thread
-
- Tags
- Mean Space Temperature
- Replies: 19
- Forum: Astronomy and Astrophysics
-

Question about space suits on Mars - for YA novel
Hi! I have a question about space suits on Mars. I've done a google search and find conflicting information. In my YA novel the protagonist makes a quick stop on Mars (just for a couple of minutes). I wonder if it's possible for a human to visit Mars surface for a couple of minutes with just...- Elon303
- Thread
- Replies: 13
- Forum: Science Fiction and Fantasy Media
-

Does light move, or does space and time move past light?
Could it be possible for light to not move at all but remain still while space and time moves past it? The light would just exists as the continuum of space time moves past light. -
E
Inverted Pendulum on a Cart -- Nonlinear State Space equations
Hi good day. I am trying to find the general Inverted Pendulum on a cart nonlinear state space equations with two degrees of freedom with x, x_dot, theta, theta_dot which represents displacement, velocity, pendulum angle from vertical, angular velocity. However from research, I am seeing...- elecboss
- Thread
- Replies: 1
- Forum: Programming and Computer Science
-
J
I Calculating the number of energy states using momentum space
A question came up about deducing the number of possible energy states within a certain momentum ##p## using momentum space. To make my question easier to understand, I deliberately chose ##p## and not a particular increment ##dp## and I assume a 2 dimensional momentum space with coordinates...- JohnnyGui
- Thread
- Replies: 153
- Forum: Quantum Physics
-
J
A Are quantum fields real objects in space?
I always had a tough time understanding how QFT relates to reality. Are these quantum fields (electron field, ect) physically real? Are they things that exist in space or are they just mathematical abstractions that help use calculate things?- JG11
- Thread
- Replies: 152
- Forum: Quantum Physics
-

Time dilation in a magnetic field
Hi all. I was wondering if time is dilated whilst traveling in a stable magnetic field that is generated by the object travelling, and if so, does this vary if you reduce or intensify the magnetic field? Also, what happens if the object is generating two opposing magnetic fields, would...- Mr C Odd
- Thread
- Replies: 7
- Forum: Special and General Relativity
-

I Space & Time Axes Coinciding: Consequences Explored
Let's consider two inertial frame S and S'. S' moves with speed v w.r.t S along x-axis towards the right. Now we can draw the two co-ordinates system. The t' axes will make an angle arctan(v/c) with t axes rotated towards x-axis and similarly the x' axis will be tilted towards the t axes...- Avi Nandi
- Thread
-
- Tags
- Axes Space Space and time Time
- Replies: 3
- Forum: Special and General Relativity
-
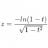
Artificial gravity in a rotating space station
It is often proposed that gravity could be simulated on a space station by rotating around an axis, such that the astronaut experiences the centripetal force of the space station wall, analogously to gravity. It is usually mentioned that the radius of rotation must be very large to avoid...- substitute materials
- Thread
- Replies: 28
- Forum: Mechanics
-
C
Russian style nuclear powered drive for a space ship?
Russia has developed a micronized nuclear powered drive for ballistic misiles and cruize misiles. This is obviously a very aggressive and environment polluting action. However, could such nuclear powered drive be used for space ships, that would start in space and do not touch the atmosphere of... -

B Space Curvature & Potential Energy
So I'm an Software Engineer, not a physicist, nor a mathematician. So I like to work in the qualitative, not the quantitative. Today I hit on a problem. I've been trying to remove the concept of "down" or "inward" from my thinking of gravity and GR. When people show the concept of space/time...- PaulCam
- Thread
- Replies: 5
- Forum: Special and General Relativity
-
Y
State Space Model of an RL Circuit
Homework Statement For the given circuits, identify state variables and derive a state-space model for each. Assume the input is v(t) and the output is vL(t). Homework EquationsThe Attempt at a Solution [/B] So my issue is that I solved this problem using two different methods. First...- YoshiMoshi
- Thread
- Replies: 1
- Forum: Introductory Physics Homework Help
-

I Energy stored in space-time or space?
I was talking to a graduate physics student about the issue of energy conservation in an expanding universe. I paraphrased the argument against energy conservation as follows - Suppose we have a photon in outer space that is very far from earth. The universe is expanding (by this I meant that in...- Euthan
- Thread
- Replies: 7
- Forum: Special and General Relativity
-

Calculate the electric field in all of space for a non conducting sphere
Homework Statement A) Use Gauss's Law to derive the electric field in all space for a non-conducting sphere with volumetric charge distribution ρ=ρ0r3 and radius, R. B) Repeat when there is a concentric spherical cavity within the non conducting sphere with radius, A. Homework Equations...- cookiemnstr510510
- Thread
- Replies: 2
- Forum: Introductory Physics Homework Help
-
D
B Space is Discrete? Argument Explored
I be grateful for any feedback on this argument: - First assume space is continuous - Then there is an actually infinite amount of information in a spatial volume of 10000 cubic units - There is also an actually infinite amount of information in a spatial volume of 1 cubic unit - But this is a...- DannyTr
- Thread
- Replies: 28
- Forum: Astronomy and Astrophysics
-
S
State Space representation of an inverted Pendulum
Homework Statement I am trying to learn how to create state space representations. I am using this link to study. http://www2.ensc.sfu.ca/people/faculty/saif/ctm/examples/pend/invpen.html Could someone explain how to get the matrix A from my equations? Homework EquationsThe Attempt at a...- shreddinglicks
- Thread
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
J
Are space fighters really impossible in realistic Sci Fi?
TL;DR at bottomIt's a somewhat accepted convention that in realistic scifi space fighters should be impossible to use effectively. In general they are regarded as being easy targets that, at interstellar ranges would be unable to survive in a battlefield that employs current plausible scifi...- Jetro
- Thread
-
- Tags
- Impossible Space
- Replies: 112
- Forum: Science Fiction and Fantasy Media
-

I Orthonormal Basis of Wavefunctions in Hilbert Space
Hello, I've a fundamental question that seems to keep myself confused about the mathematics of quantum mechanics. For simplicity sake I'll approach this in the discrete fashion. Consider the countable set of functions of Hilbert space, labeled by i\in \mathbb{N} . This set \left...- Jd_duarte
- Thread
- Replies: 2
- Forum: Quantum Physics
-

MHB 307.8.1 Suppose Y_1 and Y_2 form a basis for a 2-dimensional vector space V
nmh{796} $\textsf{Suppose $Y_1$ and $Y_2$ form a basis for a 2-dimensional vector space $V$ .}\\$ $\textsf{Show that the vectors $Y_1+Y_2$ and $Y_1−Y_2$ are also a basis for $V$.}$ $$Y_1=\begin{bmatrix}a\\b\end{bmatrix} \textit{ and }Y_2=\begin{bmatrix}c\\d\end{bmatrix}$$ $\textit{ then }$...- karush
- Thread
-
- Tags
- Basis Form Space Vector Vector space
- Replies: 8
- Forum: Linear and Abstract Algebra
-
H
B Feasibility of a L1 Gravity Swing Cold Launch?
At an L1 LaGrangian point between two bodies, one could - materials science notwithstanding - pit two of Newton's Laws (LM3,UG) against each other to provide thruster-free stationkeeping. Would it be feasible to use that to launch free from the system ? either spit out like a watermelon seed...- hmmm27
- Thread
- Replies: 18
- Forum: Other Physics Topics
-

B The geometry of the expansion of space
I've been trying to wrap my head around the geometry of the expansion of space, from Science Channel shows I vaguely understand the "every point in space is moving away from every other point in space" and iirc this was uniformly so. Is that correct? If not ignore the rest of this post I suppose...- benorin
- Thread
- Replies: 5
- Forum: Astronomy and Astrophysics
-
T
I Cooling of a hot body in the vacuum of space
In the 19th century Lord Kelvin made the first numerical calculation of the age of the Earth not based on the Bible.From his initial guess that the Earth started as a molten rock and that today the temperature of the interior increases at a certain rate as you approach the center, he got an age... -

I What is it that forces an object down curved space time?
To explain the concept of curved space time, we often use analogy of rubber sheet. If we put a heavy ball at the centre of sheet then it creates a depression and now a smaller ball will fall towards that heavy ball because of depression. But in this analogy smaller ball is falling down the slope... -

I Inner products on a Hilbert space
Hello, I am taking a quantum mechanics course using the Griffiths textbook and encountering some confusion on the definition of inner products on eigenfunctions of hermitian operators. In chapter 3 the definition of inner products is explained as follows: $$ \langle f(x)| g(x) \rangle = \int...- Decimal
- Thread
-
- Tags
- Hilbert Hilbert space Space
- Replies: 2
- Forum: Quantum Physics
-
K
I Proof of 'Any Finite Dimensional Unitary Space is Complete'?
In texts treating Hilbert spaces, it's usually given as an example that "any finite dimensional unitary space is complete", but I've found no proof so far and failed prove it myself.- kent davidge
- Thread
- Replies: 1
- Forum: Linear and Abstract Algebra
-

Describing Electronic orbit in 3D space using A matrix.
I've plotted out the trajectory of an imaginary electron in 3D; next I represent it's points with the matrix A(x1 y1 z1) "throughout it's orbit": ( -1/2 -1 1 ( -2 -1.5 2 (-1/2 2 3...- kenneththo85431
- Thread
- Replies: 5
- Forum: Electromagnetism
-

How many elements can be in an event space with two events?
Homework Statement "Do there exist any event spaces with just six elements?" Homework EquationsThe Attempt at a Solution Suppose ##F_1## is an event space with a non-trivial event ##A##. Then ##F_1=\{∅,A,A^c,Ω\}##. So ##inf(|F_1|) = 4##, since if you remove any of these events, ##F_1## is no...- Eclair_de_XII
- Thread
- Replies: 17
- Forum: Calculus and Beyond Homework Help
-
F
Complex numbers sequences/C is a metric space
Homework Statement If ##\lim_{n \rightarrow \infty} x_n = L## then ##\lim_{n\rightarrow\infty}cx_n = cL## where ##x_n## is a sequence in ##\mathbb{C}## and ##L, c \epsilon \mathbb{C}##. Homework Equations ##\lim_{n\rightarrow\infty} cx_n = cL## iff for all ##\varepsilon > 0##, there exists...- fishturtle1
- Thread
- Replies: 15
- Forum: Calculus and Beyond Homework Help
-

A Difference between configuration space and phase space
Lagrangian Mechanics uses generalized coordinates and generalized velocities in configuration space. Hamiltonian Mechanics uses coordinates and corresponding momenta in phase space. Could anyone please explain the difference between configuration space and phase space. Thank you in advance for...- sams
- Thread
- Replies: 1
- Forum: Classical Physics
-
T
Stargazing Space Station Live Video of the Earth
- Tom.G
- Thread
-
- Tags
- Earth Space Space station Video
- Replies: 6
- Forum: Astronomy and Astrophysics
-
K
I Theories without Fundamental Space and Time
Can string theory be made without time equations? According to Carlo Rovelli in his latest book "The Order of Time" https://www.amazon.com/dp/073521610X/?tag=pfamazon01-20 : "The equations of loop quantum gravity on which I work are a modern version of the theory of Wheeler and DeWitt. There...- kiki_danc
- Thread
- Replies: 50
- Forum: Beyond the Standard Models
-
M
MHB Is $s$ the unique vector that spans the solution space $L(A,0)$?
Hey! :o For a field $K$ and $1<n\in \mathbb{N}$ let $A\in K^{(n-1)\times n}$ aa matrix with rank $n-1$. For a row vector $z\in K^{1\times n}$ let $\left (\frac{A}{z}\right )\in K^{n\times n}$ be the matrix that we get if we add as the $n$-th row of the matrix $A$ the vector $z$. To show that...- mathmari
- Thread
-
- Tags
- Space
- Replies: 3
- Forum: Linear and Abstract Algebra
-
S
I How was the value of the permittivity of free space determined?
The permittivity of free space, ε0, is usually given without any derivation or historical context as to how it was experimentally determined. Could you explain to me how the value of ε0 was first determined experimentally or provide a resource that gives such a derivation? Thanks!- Steven_Scott
- Thread
- Replies: 7
- Forum: Astronomy and Astrophysics
-
W
I Debye model and reciprocal space
Hi everyone, I need a little help understanding how periodic reciprocal space applies to the Debye model for solids. Many thanks in advance! If we start with the general derivation of a dispersion relation for a 1D system, with atoms coupled by springs, one gets the following relation $$\omega...- WWCY
- Thread
- Replies: 5
- Forum: Atomic and Condensed Matter
-
S
I When should I use a plus or minus sign in space and time translations?
Hello! I am a bit confused about the sign in space and time translation operators acting on a state. I found it with both plus and minus sign and I am not sure which one to use when. The equations I am talking about are: $$U(t)=e^{\pm iHt/\hbar}$$ and $$T(x)=e^{\pm ixp/\hbar}$$. Is it a plus or...- Silviu
- Thread
-
- Tags
- Space Space and time Time
- Replies: 2
- Forum: Quantum Physics
-
A
A What volume of interstellar space is needed to form a star?
So, let me preface by saying I’m neither a scientist nor a mathematician, so am requesting some talented help here checking the accuracy of my source information and math. Regarding star formation, I got curious about how much volume of space in the interstellar medium is actually required to... -

If O is an event space, show for a finite number of events--
Homework Statement "If ##A_1,...,A_m\in O## and ##k\in ℕ##, show that the set of points in ##Ω## (the sample space) which belong to exactly ##k## of the ##A_i## belongs to ##O## (the previous exercise is the case when ##m=2## and ##k=1##)." Homework Equations Event space: O ##O\neq ∅##...- Eclair_de_XII
- Thread
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
M
I Will Space Expansion Lead to the Formation of Black Holes and Neutron Stars?
1) space is expanding at an increasing rate, therefore things are getting farther from each other and therefore increasing in velocity. 2) the faster an object moves relative to another, the more mass it has 3) supermassive objects can turn into neutron stars, black holes, etc. Therefore, will...- Meuchedet
- Thread
- Replies: 1
- Forum: Astronomy and Astrophysics
-
M
Dot product and basis vectors in a Euclidean Space
Homework Statement I am asked to write an expression for the length of a vector V in terms of its dot product in an arbitrary system in Euclidean space. Homework EquationsThe Attempt at a Solution The dot product of a vector a with itself can be given by I a I2. Does that expression only apply...- Mathematicsresear
- Thread
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

B What Secrets Does the Color of Space Hold and How Does Space Travel Work?
When we see with open eyes or in visible range of wavelength of e.m. wave we see black space containing some star...but if we see the space in other range of wavelength of the e.m. wave what will we see?? Also why the space is black?? Which matel we find in space mostly? Can we extract those...- nivamani Rajbongshi
- Thread
- Replies: 5
- Forum: Astronomy and Astrophysics
-
G
A Phase Space and Its Use in Monte Carlo Simulations of Radiation Beams
In the field of medical physics, specifically in monte carlo simulation of radiation beams produced by electron accelerators, people call ‘phase space’ to a file that contains the data of a large number of particles when they traverse a reference surface in the machine (usually a plane), i.e...- Gruxg
- Thread
- Replies: 1
- Forum: Astronomy and Astrophysics
-

Functions forming a vector space
Homework Statement 1.1.3 1) Do functions that vanish at the endpoints x=0 and L=0 form a vector space? 2) How about periodic functions? obeying f(0)=f(L) ? 3) How about functions that obey f(0)=4 ? If the functions do not qualify, list what go wrong.Homework Equations The Attempt at a...- Pushoam
- Thread
- Replies: 9
- Forum: Calculus and Beyond Homework Help