Surface integral Definition and 253 Threads
-
U
Not sure if this surface integral is right
Homework Statement The Attempt at a Solution I did the manual integration of part (i) and got an answer of 5/6 instead, I'm not sure which part is wrong.. For the surfaces, I start off with the surface in the x-z plane, then the slanted plane, then the y-z plane, then the top of the prism...- unscientific
- Thread
- Integral Surface Surface integral
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
B
Surface Integral Homework: Compute \iint_S \sin y dS
Homework Statement Compute the integral \iint_S \sin y dS where S is part of the surface x^2 +z^2 = \cos^2(y) lying between the planes y=0 and y=\pi/2. Homework Equations \iint_S f(x,y,z) dS = \iint_D f(x,y, g(x,y)) \sqrt{g_x^2 +g_y^2 +1}dA \iint_S f(x,y,z) dS = \iint_D...- BurningHot
- Thread
- Integral Surface Surface integral
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
M
Surface integral and divergence theorem over a hemisphere
Homework Statement Please evaluate the integral \oint d\vec{A}\cdot\vec{v}, where \vec{v} = 3\vec{r} and S is a hemisphere defined by |\vec{r}| \leqa and z ≥ 0, a) directly by surface integration. b) using the divergence theorem. Homework Equations -Divergence theorem in...- marineric
- Thread
- Divergence Divergence theorem Hemisphere Integral Surface Surface integral Theorem
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
D
Surface Integral - 2 methods give different answer
Thanks for checking this out. Here's the problem: I attempted to do it by using parametrize it into spherical coordinate. r(r,t) = (x= cost, y= sint, z=r) dS=|r_{u} x r_{v}| dA = r\sqrt{2} dA dA = rdrdt \int\intx^{2}z^{2}dS = \int\int\sqrt{2} cos^{2} r^{6} drdt I check my...- destroyer130
- Thread
- Integral Surface Surface integral
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
M
Why is z = rcos(θ) and not z = rsin(θ) in surface integrals?
Look in the paint doc. I was wondering why they said z = rcos(θ) and not z = rsin(θ) and x = rcos(θ)- Miike012
- Thread
- Integral Surface Surface integral
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-

How Is the Surface Area of a Rotated Curve Calculated Using Integrals?
Homework Statement Consider the surface S formed by rotating the graph of y = f(x) around the x-axis between x = a and x = b. Assume that f(x) ≥ 0 for a ≤ x ≤ b. Show that the surface area of S is 2π times integral of f(x)sqrt(1 + f ' (x)^2) dx from a to b. http://i.imgur.com/qFeGP.png...- countzander
- Thread
- Integral Surface Surface integral
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

Surface Integral setup and evaluate
Homework Statement Evaluate the surface integral ∫∫f(x,y,z)dS using an explicit representation of the surface. f(x,y,z) = x^2 + y^2;\mbox{ S is the paraboloid } z= x^2 + y^2\mbox{ for }0\leq z \leq 4 Homework Equations \displaystyle \int \int_{S} f(x,y,z)\ dS = \int \int_{D} f...- MacLaddy
- Thread
- Integral Surface Surface integral
- Replies: 11
- Forum: Calculus and Beyond Homework Help
-

Surface Integral: Find Area of Cone (0 ≤ z ≤ 4)
Homework Statement Find the area of the following surface using an explicit description of a surface. The cone z^2=4x^2+4y^2\mbox{ for } 0 \leq z \leq 4 Homework Equations \iint_s f(x,y,z)dS=\iint_R f(x,y,g(x,y))\sqrt{z^2_x+z^2_y +1} The Attempt at a Solution I have solved the...- MacLaddy
- Thread
- Integral Surface Surface integral
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
S
Surface Integral of a Cylinder
Homework Statement Let S denote the closed cylinder with bottom given by z=0, top given by z=4, and lateral surface given by the equation x^2 + y^2 = 9. Orient S with outward normals. Determine the indicated scalar and vector surface integral to ∫∫ x^2 i dS (I have tried to solve this...- Syrena
- Thread
- Cylinder Integral Surface Surface integral
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
M
MHB Another surface integral: Evaluating a Surface Integral on a Paraboloid
Here is another that I am stuck on. Please doublecheck my work, and let me know if where I am stuck is correct, or if I am on the completely wrong path. Evaluate the surface integral \(\int\int f(x,y,z)dS\) using an explicit representation of the surface. \(f(x,y,z) = x^2 + y^2;\mbox{ S is... -
M
MHB Area of Cone \(z^2 = 4x^2 + 4y^2\) 0-4: Solve & Find Answer
Hello all, I've hit a roadblock on a question regarding Surface Integrals. I seem to be having a problem conceptualizing many of these concepts. Anyway, here goes. Find the area of the following surface using an explicit description of a surface. The cone \(z^2 = 4x^2 + 4y^2\) for \(0\leq... -
Y
Surface Integral over a Cone - Stokes?
Homework Statement Homework Equations I'm guessing Stoke's Theorem? However, I'm not sure how to apply it exactly.. The Attempt at a Solution Looking at Stoke's Theorem, I'm still not sure how to apply it. I'm really just lost as to where to begin; is there even a \grad F to take? I know...- YayMathYay
- Thread
- Cone Integral Stokes Surface Surface integral
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
C
Surface integral (Flux) with cylinder and plane intersections
Homework Statement Evaluate the surface integral \int_{S} \int \vec{F} \cdot \vec{n}\,dSwith the vector field \vec{F⃗}=zx\vec{i}+xy\vec{j}+yz\vec{k} . S is the closed surface composed of a portion of the cylinder x^2 + y^2 = R^2 that lies in the first octant, and portions of the planes...- CAF123
- Thread
- Cylinder Flux Integral Plane Surface Surface integral
- Replies: 38
- Forum: Calculus and Beyond Homework Help
-
T
Parameterizing surface in surface integral problem
Homework Statement Find the area of the surface cut from the paraboloid z=2x2+2y2 by the planes z=2 and z=8.Homework Equations Surface area of S= ∫∫ ||Ts×Tt|| ds dtThe Attempt at a Solution What I am really having trouble doing in this problem (and in general) is parameterizing the surface in...- tasveerk
- Thread
- Integral Surface Surface integral
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
T
How a vol. integral becomes a vol. integral plus surface integral
Hello, Please see this pdf at some universities website: http://physics.ucsc.edu/~peter/110A/helmholtz.pdf In line 14 the author claims using integration by parts...I do not understand who could the integration by parts be used here. I understand the general case where we have... -
O
Divergence Integral doesn't equal surface integral
We were given an electric field defined by Kr^3 , and asked to calculate what the total flux would be given a sphere of a radius R. I had already calculated the divergence of E to be equal to 5kr^2 . So the first integral is calculating what the divergence over the area of the sphere is...- ozone
- Thread
- Divergence Integral Surface Surface integral
- Replies: 2
- Forum: Advanced Physics Homework Help
-
U
Evaluate this surface Integral
Homework Statement The problem is attached in the picture.The Attempt at a Solution The suggested solution went straight into the hardcore integration. I was trying a different approach by changing the variables (x,y) into (u,v) which appear to make the integration much easier... The...- unscientific
- Thread
- Integral Surface Surface integral
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-
R
Evaluate surface integral over surface
Homework Statement Evaluate the surface integral of G over the surface S S is the parabolic cylinder y=2x^2, 0=< x =<5, 0=< z =<5 G(x,y,z)=6x Answer is one of the following: 1. (15/8)*(401sqrt(401)-1) 2. (5/8)*(401sqrt(401)-1) 3. (15/8)*(401sqrt(401)+1) 4. (5/8)*(401sqrt(401)+1)...- ride4life
- Thread
- Integral Surface Surface integral
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
S
Surface Integral finding the limits
Homework Statement I need to evaulate ∫ ∫S dS where S is the surface z = x² + y², 0 ≤ z ≤ 4. Homework Equations dS = √( 1 + ƒ²x + ƒ²y)dxdyThe Attempt at a Solution dS = √( 1 + 4x² + 4y²)dxdy here's the problem what are the limits to the surface integral? no clue.. dx means i should find...- Spout
- Thread
- Integral Limits Surface Surface integral
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
R
Relationship between two surface integral equations
Homework Statement Calculate the surface integral ∫∫S x2z2 dS, where S is the part of the cone z2=x2+y2 between the planes z=1 and z=3 Homework Equations There are two relative equations for calculating surface integrals by transforming them into double integrals, but my question is about...- rrroach
- Thread
- Integral Relationship Surface Surface integral
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
Y
Computing a surface integral with polar coordinates
Homework Statement Show that ##\iint_{S}(x^2 + y^2)d\sigma = \frac{9\pi}{4}## where ##S = \{(x,y,z): x > 0, y > 0, 3 > z > 0, z^2 = 3(x^2 + y^2)\}## Homework Equations ##\iint_{S}f(x,y,z)d\sigma = \iint_{R}f(r(x,y))\sqrt{[r_x(x,y)]^2 + [r_y(x,y)]^2 + 1}## where ##r : R → ℝ^3, R \in ℝ^2##...- Yami
- Thread
- Computing Coordinates Integral Polar Polar coordinates Surface Surface integral
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-

Surface Integral of a helicoid.
Homework Statement Evaluate \int\int_{S}\sqrt{1+x^2+y^2} dS S is the helicoid with vector equation r(u,v) = <u cos(v), u sin(v), v> 0<u<2, 0<v<4pi The Attempt at a Solution If I replace the term under the radical with its vector equation counterpart, and multiply that by the...- ElijahRockers
- Thread
- Integral Surface Surface integral
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
L
Where have I gone wrong with this surface integral problem?
Homework Statement Evaluate the surface integral ∫F.dS where F = xi - yj + zk and where the surface S is of the cylinder defined by x^2+y^2≤4, and 0≤z≤1. Verify your answer using the Divergence Theorem. Homework Equations The Attempt at a Solution I parametrized the surface in...- Lucy Yeats
- Thread
- Integral Surface Surface integral
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
L
Surface Integral, flux. Boundary and orientation
In solving a flux integral over a flat surface, inclined above the xy-plane, does the boundary of the surface influence the flux only through the integral limits? (and not through its normal vector) Let's say that there is an elliptic surface inclined above the xy-plane. The orientation is... -
H
Surface integral problem from H.M. Schey's book
I've been fooling around by myself with the book "div, grad, curl and all that" by H.M. Schey to learn some vector calculus. However, in the second chapter, when he performs the integrals, he skips the part where he finds the limits on x and y. Here's an example: Compute the surface integral... -
K
Surface integral to Lateral integral?
Homework Statement I have some working out my lecture gave me to a problem and I don't think I understand part of it. Hoping you could help me. It's using Gauss' Law to find the capacitance of a cylindrical capacitor of length L but this information shouldn't matter for my question...- KingBigness
- Thread
- Integral Surface Surface integral
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
A
Surface integral or Divergence Theorem confused?
Homework Statement Find the Volume ∫∫ xy DA where R is the region bounded by by the line y=x-1 and the parabola y^2=2x+6. Homework Equations ∫∫ xy dx dy The Attempt at a Solution first i found the intersection of the above equations . which is (5,4) to (-1,-2) . then i...- abrowaqas
- Thread
- Confused Divergence Divergence theorem Integral Surface Surface integral Theorem
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
A
Surface Integral: Calculating Over a Square XY-Plane
Homework Statement Calculate the surface integral of the vector field a=xy i + (x+1) j + xz^2 k over a square in the xy-plane with length 1 and whose unit normal points in the positive direction of the z axis. Homework Equations This is the problem. There are many different types of...- aaaa202
- Thread
- Integral Surface Surface integral
- Replies: 12
- Forum: Calculus and Beyond Homework Help
-

Surface integral use stokes/divergence/whatever is convenient
Homework Statement Consider the closed surface S consisting of the graph z=1-x^2-y^2 with z \ge 0 and also the unit disc in the xy plane. Give this surface an outer normal. Compute: \int \int_s \mathbf{F} \cdot d \mathbf{S} Homework Equations Stokes theorem, divergence theorem...- ArcanaNoir
- Thread
- Integral Surface Surface integral
- Replies: 14
- Forum: Calculus and Beyond Homework Help
-
K
Time-retarded E-field and Gaussian surface integral
If I have an oscillating charge inside of a sphere, will the integral of E(t), where t=proper time of the sphere, over the sphere's surface area result in a value of electric flux equal to the value of the charge?- kmarinas86
- Thread
- E-field Gaussian Gaussian surface Integral Surface Surface integral
- Replies: 14
- Forum: Special and General Relativity
-
H
Surface integral of a cylinder
Homework Statement Evaluate the surface integral ∫A\bullet\hat{n}dS where A = z\hat{x}+x\hat{y}+3y^2z\hat{z} and S is the cylinder x^2+y^2=16 for the range of x\geq0,y\geq0, 0\leqz\leq5 Homework Equations I used this page as an example way to do this. I'm not good with surface integrals...- hover
- Thread
- Cylinder Integral Surface Surface integral
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-

Surface Integral of an Inverted Paraboloid with Radius 2 and Height 4
Homework Statement http://s1.ipicture.ru/uploads/20120118/EHTTIkiQ.jpg The attempt at a solution I've drawn the graph in my copybook. It's an inverted paraboloid with radius 2 on the xy-plane height of 4 on the z-axis, which cuts off at plane z=3. ∇\vec{\phi}=-2x\vec{i}-2y\vec{j}-\vec{k}...- DryRun
- Thread
- Integral Surface Surface integral
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
B
Evaluating a Surface Integral: xze^y i -xze^y j +z k
Homework Statement Evalute the surface integral Homework Equations F(x,y,z)=xze^y i -xze^y j +z k for the surface is partof the plane x+y+2z=2 in the first octant and orientated downwards The Attempt at a Solution \displaystyle \int \int_{\sigma} F dS=\int \int_R (xze^y i -xze^y...- bugatti79
- Thread
- Integral Surface Surface integral
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
B
Evaluating Surface Integral for Hyperboloid in Cylinder
Homework Statement Evaluate the surface integral Homework Equations f(x,y,z)=y where sigma is part of the hyperboloid y=x^2+z^2 that lies inside cylinder x^2+z^2=4 The Attempt at a Solution For \displaystyle S= \int \int_R \sqrt(z_x^2+z_y^2+1) dA I calculate...- bugatti79
- Thread
- Cylinder Integral Surface Surface integral
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
W
Surface integral of a vector field w/o div. theorem
Homework Statement First a thanks for the existence of this site, i find it quite useful but had no need to actually post till now. I am stuck on the following problem in "introduction to physics" We should calculate the \oint \vec{v}.d\vec{A} of a object with the following parameters...- wildefire
- Thread
- Field Integral Surface Surface integral Theorem Vector Vector field
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
B
Evaluating a Surface Integral: A Parallelogram
Homework Statement Evlute the surface integral Homework Equations f(x,y,z)=x+y+z where sigma is the parallelogram with parametric equations x=u+v, y=u-v and z=1+2u+v where 0 <=u<=2 and 0<=v<=1. The Attempt at a Solution I have no idea how to tackle this. Any suggestions?- bugatti79
- Thread
- Integral Parallelogram Surface Surface integral
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
B
Evaluating Surface Integral for f(x,y,z)=(x^2+y^2)zy
Homework Statement Evaluate the surface integral \displaystyle \int \int_\sigma f(x,y,z) dS for f(x,y,z)=(x^2+y^2)zy where σ is the portion of the sphere x^2+y^2+z^2=4 and abov plane z=1 The Attempt at a Solution I realize this can be done by parameterising the surface using θ and ∅...- bugatti79
- Thread
- Integral Surface Surface integral
- Replies: 14
- Forum: Calculus and Beyond Homework Help
-
J
Converting cartesian surface integral to polar
If I have an integral: \int\int_{R} x^{2} + y^{2} dy dx Where the region R is the area enclosed by a circle centered on the origin of any given radius, is it possible to just convert x^2 + y^2 to r^2 and integrate from 0 to r over dr and 0 to 2 pi over d\theta? So it would become... -
I
Surface integral problem - don't need to use Jacobian for polar?
Homework Statement Evaluate the surface integral. ∫∫S x^2*z^2 dS S is the part of the cone z^2 = x^2 + y^2 that lies between the planes z = 1 and z = 3. Homework Equations \int \int _{S}F dS = \int \int _D F(r(u,v))|r_u\times r_v|dA x=rcos(\theta) y=rsin(\theta) The Attempt...- ishanz
- Thread
- Integral Jacobian Polar Surface Surface integral
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-
D
Surface Integral of Vector fields
Homework Statement Use Stokes' Theorem to evaluate ∫C F · dr. C is oriented counterclockwise as viewed from above. F(x, y, z) = (x + y^2) i + (y + z^2) j + (z + x^2) k C is the triangle with vertices (9, 0, 0), (0, 9, 0), and (0, 0, 9). Homework Equations Stokes' Theorem The...- dancingmonkey
- Thread
- Fields Integral Surface Surface integral Vector Vector fields
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
I
Surface Integral of a Cylindrical Surface
Homework Statement What is the integral of the function x^2z taken over the entire surface of a right circular cylinder of height h which stands on the circle x^2 + y^2 = a^2 Homework Equations The Attempt at a Solution My problem is writing the equation in cylindrical form if...- Iamblu
- Thread
- Cylindrical Integral Surface Surface integral
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
X
What is the surface integral of a cone in polar coordinates?
Homework Statement g(x,y,z) = z2; Ʃ is the part of the cone z = \sqrt{x2+y2} between the planes z = 1 and z = 3. Homework Equations Conversion to polar coordinates ∫∫Ʃg(x,y,z)dS = ∫∫Rg(x,y,f(x,y)) \sqrt{fx2 + fy2+1} The Attempt at a Solution If we're talking in terms of r and θ...- XcKyle93
- Thread
- Cone Integral Surface Surface integral
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
H
Surface Integral between planes
Homework Statement ∫∫s x √(y2 + 4) where S: y2 + 4z = 16, and portion cut by planes x=0, x=1, z=0. Homework Equations I attempted to solve using the surface area integral formula, whereby this double integral is transformed to ∫∫f(x,y,g(x,y)) √((∂z/∂x)2 + (∂z/∂y)2 + 1) dA The...- hooshies
- Thread
- Integral Planes Surface Surface integral
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

Surface Integral Calculation for Parabolic Cylinder on Circular Area
How do i calculate the surface integral ∫∫xdS where z=x^{2} is the parabolic cylinder over the area x^{2}+y^{2}=1I do not know how to solve this task because i can't express the surface parametrization in r(x,y). But when i express it as g(x,z)=0 i get the double integral dependet on dxdz...- beyondlight
- Thread
- Integral Surface Surface integral
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
N
Variable conversion in surface integral
Hello helpful fellas, I'm reading an ecological model that involves setting up boundaries conditions. As part of a longer derivation, there is this flux equation (seen in attachment). Since I haven't formally studied vector calculus, please educate me in how it works and preferably with... -
M
Surface Integral: dot product of two unit vectors
Hello. :smile: I understand most of the work involved with these types of questions, but there is one point in an example I'm following that I don't understand. Homework Statement Evaluate: I = \int{(z^2)}dS over the positive quadrant of a sphere, where (x,y > 0). Homework...- Matty R
- Thread
- Dot Dot product Integral Product Surface Surface integral Unit Unit vectors Vectors
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
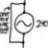
Electric field vector & surface integral
Homework Statement See figure attached. Homework Equations The Attempt at a Solution See figure attached. The solution shows that, \vec{r} = x \hat{i} + y \hat{j} + z \hat{k} How did they obtain this?- jegues
- Thread
- Electric Electric field Field Integral Surface Surface integral Vector
- Replies: 9
- Forum: Introductory Physics Homework Help
-
D
Surface integral of normal vector
Hi. Does anyone know how to prove that \int \int dS \hat \mathbf n = \int \mathbf r \times d\mathbf r i.e., the surface integral of the unit normal vector equals the line integral on the r.h.s. ?- daudaudaudau
- Thread
- Integral Normal Surface Surface integral Vector
- Replies: 6
- Forum: Calculus
-
M
Surface Integral over Half Shell
From Div,Grad, Rot and all that Disclaimer: Sorry, why do the Latex tags not work? Homework Statement "An electrostatic field is given by \vec{E} = \lambda (\hat{\vec{i}}yz + \hat{\vec{j}}xz + \hat{\vec{k}}xy), where \lambda is a constant. Use Gauss' law to find the total charge enclosed by a...- mzh
- Thread
- Integral Shell Surface Surface integral
- Replies: 19
- Forum: Calculus and Beyond Homework Help
-
A
Surface Integral: Solving for Unknown Functions | Homework Help
Homework Statement Homework Equations The Attempt at a Solution How to integrate this function?- athrun200
- Thread
- Integral Surface Surface integral
- Replies: 2
- Forum: Calculus and Beyond Homework Help