Taylor series Definition and 480 Threads
-
A
Taylor Series Expansion for f(z) = −1/z^2 about z = i + 1
Homework Statement Find the Taylor series expansions for f(z) = −1/z^2 about z = i + 1. Homework Equations The Attempt at a Solution I'm just not sure what format I'm supposed to leave it in. Is it meant too look like this: f(z)=f(i+1)+f'(i+1)(x-i-1)... or this Ʃ\frac{1}{n!}f^{(n)}(1+i) *...- Applejacks
- Thread
- Expansion Series Series expansion Taylor Taylor series
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
N
Taylor series and second derivative test: the degenerate case.
Hello! I am wondering if someone could let me know if my understanding is right or wrong. The Taylor series gives the function in the form of a sum of an infinite series. From this an approximation of the change in the function can be derived: f_{a} and f_{a,a} are the first and second... -
A
What is the trick to simplifying the Taylor series of 1/(1 + x^2)?
The equation starts at B and this is my attempt. As you can see it soon complicates and doesn't look like what t should since I already know what the Taylor series of his function should look like. Is there some clever trick to it that I am missing? PS the series is centred around x = 0... -
O
Taylor Series: Show Terms Decay as 1/n^2
Show that, with an appropriate choice of constant c, the taylor series of (1+cx)ln(1+x) has terms which decay as 1/n^2 I know that ln(1+x) decays as 1/n, but I don't know how to show the above. Please help. Thanks in advance- optics101
- Thread
- Series Taylor Taylor series
- Replies: 4
- Forum: General Math
-
D
How can the Taylor series help prove the limit of cosine?
I have to prove that \cos(x) = 1 - \frac{x^2}{2} + O(x^4) (x \to 0) My ugly attempt: \lim_{x \to 0} \frac{\cos(x) - 1 + \frac{x^2}{2}}{x^4} \lim_{x \to 0} \frac{\cos(x) - 1}{x^4} + \frac{1}{2x^2} \lim_{x \to 0} \frac{\sin(x)}{4x^3} + \frac{1}{2x^2} \lim_{x \to 0}...- Damidami
- Thread
- Series Taylor Taylor series
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
J
Finding Taylor Series - different Method
Homework Statement Hello, I'm in the middle of solving for the Taylor series of the function: f(x)=sin(2x)ln(1-x) up to n = 4. The Attempt at a Solution So far, I've been strictly taking its derivatives until I reach the fourth. It's becoming a very long process considering it's...- JaeKyung
- Thread
- Method Series Taylor Taylor series
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
N
Complex analysis, taylor series, radius of convergence
Homework Statement For f(z) = 1/(1+z^2) a) find the taylor series centred at the origin and the radius of convergence. b)find the laurent series for the annulus centred at the origin with inner radius given by the r.o.c. from part a), and an arbitrarily large outer radius. Homework...- nugget
- Thread
- Analysis Complex Complex analysis Convergence Radius Radius of convergence Series Taylor Taylor series
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
R
Taylor series and the forward finite difference method
Given a partial differential equation, how would one go about implementing the forward finite difference method to the Taylor series?- roldy
- Thread
- Difference Finite Finite difference Finite difference method Method Series Taylor Taylor series
- Replies: 2
- Forum: Differential Equations
-
C
Taylor Series : How to determine coefficient
Homework Statement https://skydrive.live.com/?cid=6b041751c72e14ad#!/?cid=6b041751c72e14ad&sc=photos&uc=3&id=6B041751C72E14AD%21149!cid=6B041751C72E14AD&id=6B041751C72E14AD%21154&sc=photos The Attempt at a Solution...- cyt91
- Thread
- Coefficient Series Taylor Taylor series
- Replies: 13
- Forum: Calculus and Beyond Homework Help
-
R
Using Taylor Series for Initial Value Problems
Homework Statement I posted this already but decided to revive this thread since I re-worked the problem. Consider dy/dx=x+y, a function of both x and y subject to initial condition, y(x0)=y0. Use Taylor series to determine y(x0+\Deltax) to 4th order accuracy. Initial condition: x0=0...- roldy
- Thread
- Homework Series Taylor Taylor series
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
T
Expansion of Taylor series for statistical functionals
Hi By some googling it seems like there exist some kind of expansion of the Taylor series for statistical functionals. I can however, not sort out how it is working and what the derivative-equivalent of the functional actually is. My situation is that I have a functional, say \theta which...- Testguy
- Thread
- Expansion Functionals Series Statistical Taylor Taylor series
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
G
Calculus II - Taylor Series Question
Homework Statement Find the power series for f(x) using the definition of taylor series expansion about a=9. f(x)=1/sqrt(x) Homework Equations The Attempt at a Solution Find the power series for f(x) using the definition of taylor series expansion about a=9. f(x)=1/sqrt(x) f(x) =...- GreenPrint
- Thread
- Calculus Calculus ii Series Taylor Taylor series
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
G
How Accurate is the Taylor Polynomial for Approximating Sin Functions?
New Question (Changed Old one) - Taylor Polynomial - Upper Bound for Absolute Error Homework Statement (a) Find the 3-rd degree Taylor polynomial of sin(pix) centered at x=1. (b) Use (a) to approximate sin(1.1*pi) (c) Use the remainder term to find an upper bound for the absolute error in...- GreenPrint
- Thread
- Calculus Calculus ii Series Taylor Taylor series
- Replies: 18
- Forum: Calculus and Beyond Homework Help
-
G
Calculus II - Taylor Series - Error Bounds
Homework Statement Hi, I'm really struggling with trying to come up with the error bound when doing taylor series problems Use the reaminder term to estimate the absolute error in approximating the following quantitites with the nth-order Taylor Polynomial cnetered at 0. Estimates are...- GreenPrint
- Thread
- Bounds Calculus Calculus ii Error Series Taylor Taylor series
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
V
Examining the Taylor Series - Confused?
hello, I'm examinating the theorem of power series, specially taylor series I know a function f(x) can be written as a series of polynomials. but using the taylor series it says that the convergence of that function is about a point a by using the Maclaurinseries a = 0 , so examinating...- vrc
- Thread
- Confused Series Taylor Taylor series
- Replies: 2
- Forum: Linear and Abstract Algebra
-
C
Multi-Variable Second Order Taylor Series Expansion: Ignoring Terms
So I'm computing a second order Taylor series expansion on a function that has multiple variables. So far I have this I(x,y,t)=dI/dx(change in x)+dI/dy(change in y)+dI/dt(change in t)+2nd order terms Would it still be a better approximation than just he first order if I included some...- cvanloon
- Thread
- Expansion Multi-variable Second order Series Series expansion Taylor Taylor series Terms
- Replies: 6
- Forum: Differential Equations
-
N
Help with Taylor Series problem
Now although this is a problem for my EE course, it is more of a calculus question so I figured I would receive the best answers by posting it in this section. I have just started on the problem but could use some input on my thoughts. So here we go (there are two parts): (problem screenshot is...- NHLspl09
- Thread
- Series Taylor Taylor series
- Replies: 20
- Forum: Calculus and Beyond Homework Help
-
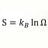
Taylor Series for Any (x) = Function (x) for Any (x) ?
When a Taylor Series is generated from a functions n derivatives at a single point, then is that series for any value of x equal to the original function for any value x ? For example graph the original function (x) from x= 0 to x = 10. Now plug into the Taylor Expansion for x , values...- morrobay
- Thread
- Function Series Taylor Taylor series
- Replies: 2
- Forum: General Math
-
F
Taylor series (very easy but have a problem)
Homework Statement series expansion at c=2 of ln(x^2+x-6) Homework Equations The Attempt at a Solution After substituting y= x -2 we get ln(y^2+5y) = ln(y) + ln(y+5) but I am not kinda sure how to use the taylor series of ln(1+x)...- FermatPell
- Thread
- Series Taylor Taylor series
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
G
Understanding the Derivation of Taylor Series
I read wikipedia article also but I can't find the proof of taylor series and from where it came from??- gursimran
- Thread
- Series Taylor Taylor series
- Replies: 2
- Forum: General Math
-
S
Calculating Remainders for Taylor Series of Sine Function
Usually to do the remainder we take Rn(x) = (f differentiated n+1 times at a ).(x-c)n+1/(n+1)!, but when my function is sin(x) do i take (f differentiated 2n+2 times at a ).(x-c)2n+2/(2n+2)!? Thanks -
S
Taylor Series for Cosine and Accuracy of Calculating Cosine 2
Homework Statement How many terms of the taylor series of the cosine function about c = 0 are needed to calculate cosine 2 to an accuracy of 1 / 10000 The Attempt at a Solution I have said that |Rn(2)| = |cosn+1(a) 2n+1/(n+1)!|<2n+1/(n+1!) Now i can't do it ...- stukbv
- Thread
- Cosine Series Taylor Taylor series
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
S
Continuum Conversion of Lattice Points via Taylor Series Expansion
I consider an array of lattice points and construct a vector at each lattice points. How to convert this discrete system into a continuum one by using the Taylor series expansion by considering the lattice distance say \lambda? thanks in well advance?- saravanan13
- Thread
- Continuum Expansion Lattice lattice points Points Series Series expansion Taylor Taylor series
- Replies: 2
- Forum: Calculus
-
M
What is the correct method for composing Taylor series at a non-zero point?
in general I'm trying to figure out a way to work with taylor series more efficiently. this means i want to be able to write down the taylor series of a complicated function just by knowing the taylor series(es?) of the component functions. I've figured out how to do products and quotients... -
D
Proving extrema using taylor series and Hessian Matrix
How do I use Taylor Series to show f(P) is a local maximum at a stationary point P if the Hessian matrix is negative definite. I understand that some of the coefficients of the terms of the taylor series expansion are the coordinates of the Hessian matrix but for the f_xy term there is no...- dispiriton
- Thread
- Extrema Hessian Hessian matrix Matrix Series Taylor Taylor series
- Replies: 4
- Forum: Linear and Abstract Algebra
-
I
Solve Taylor Series Questions with Expert Guidance | Get Help Now!"
Solved Thanks guys- irunshow
- Thread
- Series Taylor Taylor series
- Replies: 23
- Forum: Calculus and Beyond Homework Help
-
D
Taylor series centered at c = 1
Homework Statement Find the Taylor Series of 1/x centered at c = 1. Homework Equations \sum_{n=0}^{\infty} f^n (c) \frac{(x-c)^n}{n!} The Attempt at a Solution I made a list of the derivatives: f(x) = 1/x f'(x) = -1/x2 f''(x) = 2/x3 f'''(x) = -6/x4 f(1) = 1 f'(1) =...- DrummingAtom
- Thread
- Series Taylor Taylor series
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
R
What is the Taylor series expansion for (1 + x)^.5 and its derivatives?
Homework Statement a. Find the first four nonzero terms in the Taylor series expansion about x = 0 for f(x) = (1+x)^.5 b. Use the results found in part (a) to find the first four nonzero terms in the Taylor series expansion about x= 0 for g(x) = (1 + x^3)^.5 c. Find the first four...- rjs123
- Thread
- Series Taylor Taylor series
- Replies: 12
- Forum: Calculus and Beyond Homework Help
-
L
Finding the Interval of Convergence for the Taylor Series of ln(x) at a=7
Homework Statement The Taylor series of function f(x)=ln(x) at a=7 is given by: f(x)=\sum^{\infty}_{n=0}c_{n}(x-7)^{n} Determine the interval of convergence The Attempt at a Solution I have worked out that the series would be of the form...- lxman
- Thread
- Series Taylor Taylor series
- Replies: 13
- Forum: Calculus and Beyond Homework Help
-
S
Solving the Taylor Series for e^(-x^2): Is it the Same at x=0?
Do you just replace the x's with (x-3)'s? Since e^(-x^2) is defined as the taylor series though, it seems like the answer should be the same as the series about x=0. Thanks! P.S. does anyone know how to resize images? :$- sparkle123
- Thread
- Series Taylor Taylor series
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
L
Coefficients of a Taylor Series
Homework Statement The function f(x)=ln(10-x) is represented as a power series: \sum^{\infty}_{n=0}a_{n}x^{n} Find the first few coefficients in the power series. Hint: First find the power series for the derivative of . The Attempt at a Solution Okay, start seems fairly...- lxman
- Thread
- Coefficients Series Taylor Taylor series
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-

Taylor series for the following
I have a couple of general questions, combined with this one specific question Homework Statement Find the Taylor or MacLauren series centered about the given value for the following function, determine the radius of convergence Homework Equations \mathrm{Ln}\ z, 2 The Attempt at a Solution...- TheFerruccio
- Thread
- Series Taylor Taylor series
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
V
Find the taylor series of ln(1+x)
Homework Statement find the taylor series of ln(1+x) centered at zero Homework Equations from 0 to infinity ∑ cn(x-a)n cn = f(n)(a)/n! The Attempt at a Solution f(x) = ln(1+x) f'(x) = 1/(1+x) f''(x) = -1/(1+x)2 f'''(x) = 2/(1+x)3 f''''(x) = -6/(1+x)4 f(0) = 0...- vande060
- Thread
- Series Taylor Taylor series
- Replies: 5
- Forum: Introductory Physics Homework Help
-
M
Finding Taylor series for x^3 at a = -1
Homework Statement Find the Taylor series for f(x) centered at the given value of a. (Assume that f has a power series expansion. Do not show that Rn(x)--> 0.) f(x) = x^3, a = -1Homework Equations f(x) = f(a)+f'(a)(x-a)+(f''(a)/2!)(x-a)^2+(f'''(a)/3!)(x-a)^3+...+(f(nth...- mcdowellmg
- Thread
- Series Taylor Taylor series
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
E
Calculating Circle of Convergence for f(z) = (3z+1)/(15+2z-z^{2}) at z=1
Homework Statement Expand f(z) = (3z+1)/(15+2z-z^{2}) at z=1 and find the circle of convergence. Homework Equations The Attempt at a Solution I think this is pretty straight forward, but I want to make sure I'm doing everything correctly. I used a power series...- elimenohpee
- Thread
- Complex Series Taylor Taylor series
- Replies: 11
- Forum: Calculus and Beyond Homework Help
-
L
Taylor series analysis question
Homework Statement [PLAIN]http://img822.imageshack.us/img822/427/scangj.jpg Homework Equations The Attempt at a Solution Hi, could anyone help me with part b of this question, part a I have completed, however I seem to be drawing a blank on the second part- LHS
- Thread
- Analysis Series Taylor Taylor series
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
T
Convergence of a Taylor Series
Homework Statement Suppose that: sum [a_n (n-1)^n] is the Talyor series representation of tanh(z) at the point z = 1. What is the largest subset of the complex plane such that this series converges? Note: 'sum' represents the sum from n=0 to infinity Homework Equations tanh(z) =...- tylerc1991
- Thread
- Convergence Series Taylor Taylor series
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
L
Master Taylor Series with Expert Tips | F(E) = E/(KT) + (Ec/E)^1/2
Homework Statement Expand the function f(E) as a Taylor series.Homework Equations f(E)=E/(KT)+(Ec/E)1/2 The Attempt at a Solution E=Eo So it says that F(E)~Ao+A1(E-Eo)+A2(E-Eo)2... I need to find out what Ao A1 and A2 are, but not sure how to do that. It says as a hint that A1=0 becasue f(E)...- leonne
- Thread
- Series Taylor Taylor series
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
F
Taylor series for the general distance integral
Background: I'm trying to transform the gaussian distribution from flat space to curved space. I start with the flat, 1D gaussian distribution in the form \[{\textstyle{1 \over {{{(\pi {\Delta ^2})}^{{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em... -
K
Approximating sin13 with Taylor Series using TI84 (n=150)
Homework Statement approximate sin13 by using the Taylor series using the TI84. Add for n=150 Homework Equations the infinite sums for sinx is ((-1)^n)(x^(2n+1)/(2n+1)!) The Attempt at a Solution I'm new to programming so i don't have any idea on where to start. I was...- kakashi1027
- Thread
- Program Series Taylor Taylor series
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
H
How can Taylor Series help us find a value of h for a specific error tolerance?
how would you use Taylor Series to answer this: Find a value of h such that for |x|<h implies sin(x)=x-x^3/6 +x^5/120 + R where |R|< 10^-4? -
B
Finding the First Three Terms of exp(z sin z) Taylor Series
find the first three non zero terms in the Taylor Series about z=0 of exp(z sin z) i have little idea how to even start on the question because it is exp to the power of z sin z and it just looks too complicated. i hav tried looking thru txtbooks for something similar but no similar question...- blueyellow
- Thread
- Series Sin Taylor Taylor series Terms
- Replies: 1
- Forum: Introductory Physics Homework Help
-
H
I need a method to calculate ln(x) for small x, other than Taylor series method
I'm aiming to calculate ln(x) numerically. I'm using the following procedure for this: 1) If x is greater or equal to 1, use Newton's method. 2) If x is smaller between 0 and 1, use Taylor series expansion. Newton's method works good, but I have problems with Taylor series expansion method...- hkBattousai
- Thread
- Method Series Taylor Taylor series
- Replies: 12
- Forum: General Math
-
First Order Error Analysis (Taylor Series)
Homework Statement The equation for the velocity of a falling parachutist can be computed by, v(t) = \frac{gm}{c}(1-e^{-(\frac{c}{m})t}) Use a first-order error analysis to estimate the error of v at t = 6, if g = 9.8 and m = 9.8, c = 12.5 plus or minus 1.5. Homework Equations...- jegues
- Thread
- Analysis Error Error analysis First order Series Taylor series
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
F
Bounding the Error in Taylor Series Approximations for ln(1+x)
Had a recent homework questions: Find a bound for the error |f(x)-P3(x)| in using P3(x) to approximated f(x) on the interval [-1/2,1/2] where f(x)=ln(1+x) abd P3(x) refers to the third-order Taylor polynomial. I found the Taylor series of f(x) seen below: x- x^2/2!+(2x^3)/3! I know...- francisg3
- Thread
- Bound Error Series Taylor Taylor series
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

Computing true percent relative error (Taylor Series)
Homework Statement See figure attached, Homework Equations The Attempt at a Solution Isn't the Maclaurin series just simply the Taylor series around 0? (\text{i.e. } (x-c), \quad c=0, \quad x ) Also for part B, how do we go about solving for | \epsilon_{t} |? Thanks...- jegues
- Thread
- Computing Error Percent Relative Series Taylor series
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
G
Uses of power series as opposed to taylor series
So we can use the Taylor's theorem to come up with a Taylor series represent certain functions. This series is a power series. So far (I'm in my second year of calc, senior in high school), I've never seen a power series that wasn't a Taylor series. So are all power series taylor series? Whether...- gsingh2011
- Thread
- Power Power series Series Taylor Taylor series
- Replies: 2
- Forum: Calculus
-
S
Taylor Series for 1/(1+x^2) without Substitution
Homework Statement How do we get that the Taylor Series of 1/(1+x^2) around x= 0 is 1 - x^2 + x^4 + ... + (-1)^n x^{2n} + ... for |x|<1, without using a substitution of x=-x^2 into the Taylor series for 1/(1-x)? Homework Equations The Attempt at a Solution- sparkle123
- Thread
- Series Taylor Taylor series
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
W
Taylor series for cartesian circle equation
Hello. For a physics course, I need to often make use of the binomial series and it's corollary, the expansion of: \sqrt{1-x^2} This probably sounds rather stupid, but for some reason, when I do a MacClaurin expansion of this series, I cannot seem to generate the correct series, which I... -
K
Taylor series of this function
I have a homework question like this. "Find the taylor series of the function f(x) = (x2+2x+1)/(x-6)2(x+2) at x=2" I'm trying to simplify this expression so I can take the derivative. I only got this far: (x+1)(x+1)/(x-6)(x-6)(x+2) Can this be simplified more so that I can easily...- Kuzu
- Thread
- Function Series Taylor Taylor series
- Replies: 7
- Forum: Calculus and Beyond Homework Help