Transformation Definition and 1000 Threads
-
P
Do Linear Operators Equate on All Vectors if They Match on a Basis Set?
Suppose that T1: V → V and T2: V → V are linear operators and {v1, . . . , vn} is a basis for V . If T1(vi) = T2(vi ), for each i = 1, 2, . . . , n, show that T1(v) = T2(v) for all v in V . I don't understand this question. They said If T1(vi) = T2(vi ), for each i = 1, 2, . . . , n...- pyroknife
- Thread
- Basis Linear Linear transformation Transformation
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
C
Linear Transformation: Solving Coefficient Matrix and Evaluating T(e1) and T(e2)
I attached the problem. I'm not sure if I'm misinterpreting the question, but this problem seems really easy, which is usually not the case with my class. for part a) isn't that just the coefficient matrix of the right hand side? This makes A: 1 -2 3 1 0 2 for part b) T(e1)=T[1...- Clandry
- Thread
- Linear Linear transformation Transformation
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
A
Canonical transformation for Harmonic oscillator
Find under what conditions the transformation from (x,p) to (Q,P) is canonical when the transformation equations are: Q = ap/x , P=bx2 And apply the transformation to the harmonic oscillator. I did the first part and found a = -1/2b I am unsure about the next part tho: We have the...- aaaa202
- Thread
- Canonical transformation Harmonic Harmonic oscillator Oscillator Transformation
- Replies: 1
- Forum: Advanced Physics Homework Help
-
I
Transformation properties of derivative of a scalar field
Hi all, I'm a part III student and taking the QFT course. The following seems "trivial" but when I went and asked the lecturer, the comment was that they too hate such nitty gritty details! The problem is page 12 of Tong's notes: http://www.damtp.cam.ac.uk/user/tong/qft/one.pdf All...- ianhoolihan
- Thread
- Derivative Field Properties Scalar Scalar field Transformation
- Replies: 40
- Forum: Quantum Physics
-
C
Prove that this is a linear transformation
The problem statement has been attached. To show that T : V →R is a linear function It must satisfy 2 conditions: 1) T(cv) = cT(v) where c is a constant and 2) T(u+v) = T(u)+T(v) For condition 1) T(cv)=∫cvdx from 0 to 1 (I don't know how to put limits into the integral...- charlies1902
- Thread
- Linear Linear transformation Transformation
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
T
A simple application of a liner transformation
Let T: P2(ℝ) --> P2(ℝ) be defined by T(p(x)) = p( x-1) a) Find the matrix of T with respect to the standard basis of P2(ℝ) Question: So I know how to do this for the most part, I'm just having a problem in terms of the constant 1 from the standard basis of {1, x , x2 from P2(ℝ)...- trap101
- Thread
- Application Transformation
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
A
Matrix corresponding to linear transformation is invertible iff it is onto?
Let A be a nxn matrix corresponding to a linear transformation. Is it true that A is invertible iff A is onto? (ie, the image of A is the entire codomain of the transformation) In other words, is it sufficient to show that A is onto so as to show that A is invertible? That was what my...- Aziza
- Thread
- Linear Linear transformation Matrix Transformation
- Replies: 1
- Forum: Linear and Abstract Algebra
-
M
Analyzing a coordinate transformation
In McCauley's book Classical Mchanics: Transformations, Flows, Integrable and Chaotic Dynamics we are analyzing a coordinate transformation in order to arrive at symmetry laws. A coordinate transformation is given by q_i(\alpha) = F_i(q_1,...,q_f, \alpha). Then, to the first order Mccauley...- mjordan2nd
- Thread
- Coordinate Coordinate transformation Transformation
- Replies: 4
- Forum: Classical Physics
-

MHB Linear Algebra: Kernel & Range of Linear Transformation
Why are we interested in looking at the kernel and range (image) of a linear transformation on a linear algebra course?- matqkks
- Thread
- Linear Linear transformation Transformation
- Replies: 1
- Forum: Linear and Abstract Algebra
-
A
Show condition for canonical transformation
Homework Statement Consider the transformation from the variables (q,p) to (Q,P) by virtue of q = q(Q,P), p = p(Q,P) and H(q,p,t) = H(Q,P,t). Show that the equations of motion for Q,P are: \partialH/\partialQ = -JDdP/dt \partialH/\partialP = JDdQ/dt where JD is the Jacobian determinant...- aaaa202
- Thread
- Canonical transformation Condition Transformation
- Replies: 12
- Forum: Advanced Physics Homework Help
-
A
A question about linear algebra (change of basis of a linear transformation)
Homework Statement Let A \in M_n(F) and v \in F^n. Let v, Av, A^2v, ... , A^{k-1}v be a basis, B, of V. Let T:V \rightarrow V be induced by multiplication by A:T(w) = Aw for w in V. Find [T]_B, the matrix of T with respect to B. Thanks in advance Homework Equations...- Artusartos
- Thread
- Algebra Basis Linear Linear algebra Linear transformation Transformation
- Replies: 15
- Forum: Calculus and Beyond Homework Help
-
Z
Coordinate Transformation in Special Relativity with Linear Algebra Part A
Homework Statement In the figure, let S be an inertial frame and let S' be another frame that is boosted with speed v along its x'-axis w.r.t. S, as shown. The frames are pictured at time t = t0 = 0: A) Find the Non-relativistic transformation (Galilean Transformation) between the two...- zellwwf
- Thread
- Algebra Coordinate Coordinate transformation Linear Linear algebra Relativity Special relativity Transformation
- Replies: 14
- Forum: Introductory Physics Homework Help
-
T
How to Transform Dual Vector Fields: Understanding the Notation and Rules
Homework Statement Let va be a dual vector field. Show that the quantity ∂[a vb] transforms as a type (0, 2) tensor under coordinate transformations. Homework Equations wu' = (dxu / dxu') wu The Attempt at a Solution My main problem is that I don't know what the brackets mean...- tourjete
- Thread
- Dual Transformation Vector
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
M
Cumulative distribution transformation
Homework Statement Let F be the cumulative distribution function of a random variable X. Find the cumulative distribution function of Y= {\alpha}X+\beta, where \, \alpha \gt 0 Homework Equations The Attempt at a Solution I think this a fairly easy question, I just want to make...- mrkb80
- Thread
- Distribution Transformation
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
Z
Transformation + root of a quadratic.
Homework Statement 2sqrt (x^2-2), sqrt (4(x^2-2)), x^2. The first 2 formulas are the same thing. However I want to how I would explain the transformation of x^2 to either or of those. I have tried a myriad of things to try get x^2 to any of those other two graphs. A quick answer would be...- zaddyzad
- Thread
- Quadratic Root Transformation
- Replies: 2
- Forum: Precalculus Mathematics Homework Help
-

Lorentz transformation and Pythagoras' theorem
Hello, I was just going through some writings on the web reg.Lorentz transformation. Even considering the derivative factor,d, is anyway Lorentz transformation is some way, linked with Pythagoras' theorem? Correct me if I am wrong? -- Shounak- shounakbhatta
- Thread
- Lorentz Lorentz transformation Pythagoras Theorem Transformation
- Replies: 5
- Forum: Special and General Relativity
-

MHB Linear Transformation in Linear Algebra: Impact & Motivation
How important are linear transformations in linear algebra? In some texts linear transformations are introduced first and then the idea of a matrix. In other books linear transformations are relegated to being an application of matrices. What is the best way of introducing linear transformation...- matqkks
- Thread
- Linear Linear transformation Transformation
- Replies: 2
- Forum: Linear and Abstract Algebra
-

What is the importance of linear transformations in linear algebra?
How important are linear transformations in linear algebra? In some texts linear transformations are introduced first and then the idea of a matrix. In other books linear transformations are relegated to being an application of matrices. What is the best way of introducing linear transformation...- matqkks
- Thread
- Linear Linear transformation Transformation
- Replies: 4
- Forum: Linear and Abstract Algebra
-
S
Lineal Transformation basis change
Find http://imageshack.us/a/img35/1637/lineal2.gif http://imageshack.us/a/img210/1370/lineal1.gif C^3 is the canonical base of ℝ^3, C^2 is the canonical base of ℝ^2 I tried: http://imageshack.us/a/img822/6274/lineal3.gif But I'm not sure if this is right, I made a...- SqueeSpleen
- Thread
- Basis Change Transformation
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
M
Standard Normal Dist Transformation
Homework Statement The question ask to find E[X]; E[X^2]; Var(X) for the standard normal distribution f(x)=1/\sqrt{2\pi}e^{-x^2/2}Homework Equations I found \begin{align} E[X]&=\int_{-\infty}^\infty \! x*1/\sqrt{2\pi}e^{-x^2/2} \, \mathrm{d} x\\ &=1/\sqrt{2\pi} ( \int_{-\infty}^0 \...- mrkb80
- Thread
- Normal Standard Transformation
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-
D
Linear Transformation from R^m to R^n: Mapping Scalars to Vectors
Can we think of a linear transformation from R^m-->R^n as mapping scalars to vectors? Let me say what I mean. Say we have some linear transformation L from R^m to R^n which can be represented by a matrix as follows: L=[ a11x1+a12x2+...+a1mx m a21x1+... . . . anmx1+...+ anmxm...- dumbQuestion
- Thread
- Linear Linear transformation Mapping Scalars Transformation Vectors
- Replies: 3
- Forum: Calculus
-
C
Confused on how to set up my S and S' frames for Lorentz Transformation
1. The question states: "Two lights are placed along the x-axis at positions x1 = 3.00 m and x2 = 5.00 m. The lights flash at times t1 = 1.00 ns and t2 = 9.00 ns. An observer in a rest frame moving to the right sees the lights flash in the same location. Assume that the origins of the two rest...- cubano07
- Thread
- Confused Frames Lorentz Lorentz transformation Set Transformation
- Replies: 2
- Forum: Introductory Physics Homework Help
-
X
Help with coordinate transformation problem
Homework Statement For elliptical cylindrical coordinates: x = a * cosh (u) * cos (v) y = a * sinh (u) * sin (v) z = z Derive the relations analogous to those of Equations (168b-e) for circular cylindrical coordinates. In particular, verify that h_u = h_v = a * sqrt(cosh^2 (u) -...- xiphius75
- Thread
- Coordinate Coordinate transformation Transformation
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
H
Coordinate system transformation
Can someone help me with the conversion of this equation to Cartesian coordinates: [SIZE="4"]2cosθr + sinθθ (Due to formatting limitations, I just made the r_hat and theta_hat components bold-faced) I know the answer ought to be -(3y2)/[(x2+y2)+1] but I've tried every variation of the 3 main... -
T
Norton Equivalent and Source Transformation problem
Homework Statement Basically, I'm having trouble doing the source transformation and subsequently finding the norton equivalent for this circuit and I don't really know where to start. The circuit is attached where: i=3A V=90V Please help!- tjenk48
- Thread
- Equivalent Norton equivalent Source Source transformation Transformation
- Replies: 1
- Forum: Introductory Physics Homework Help
-
S
Lorentz transformation Problem, Confused on setting it up
So this is my first course in upper level physics, and I'm still trying to figure out special relativity. The problem: Two events occur at the same place in a certain inertial frame and are separated by a time interval of 4sec. What is the spatial separation between these two events in an...- sealsix14
- Thread
- Confused Lorentz Lorentz transformation Transformation
- Replies: 3
- Forum: Special and General Relativity
-
D
Example of a linear transformation L which is injective but not surj, or vice versa
Homework Statement Give an example of a linear vector space V and a linear transformation L: V-> V that is 1.injective, but not surjective (or 2. vice versa) Homework Equations -If L:V-> V is a linear transformation of a finitedimensional vector space, then L is surjective, L is...- damabo
- Thread
- Example Injective Linear Linear transformation Transformation
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
P
Transformation of random variable
Hi there, I am currently reading Rohatgi's book "An introduction to probabilty and statistics" (http://books.google.de/books?id=IMbVyKoZRh8C&lpg=PP1&hl=de&pg=PA62#v=onepage&q&f=true). My questions concerns the "technique" of finding the PDF of a transformed random varibale Y by a function...- philipp_w
- Thread
- Random Random variable Transformation Variable
- Replies: 7
- Forum: Set Theory, Logic, Probability, Statistics
-
B
Linear Transformation: find dilating/rotation matrix
Homework Statement The vector A has length 8.5, and makes an angle of 5pi/19 with the x-axis. The vector B has length 6, and makes an angle of 8pi/19 with the x-axis. Find the matrix which rotates and dilates vector into vector . Homework Equations Rotation matrix in...- bcahmel
- Thread
- Linear Linear transformation Matrix Transformation
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
S
Special Relativity - Velocity transformation problem
Homework Statement Two spaceships are moving away from Earth at a speed of 0.8c, with one ship following in the flight path of the other. Their separation along the axis of their motion is maintained at 0.1 light years as measures by the spaceships' instruments. A crew exchange vehicle is...- seasponges
- Thread
- Relativity Special relativity Transformation Velocity Velocity transformation
- Replies: 3
- Forum: Introductory Physics Homework Help
-
D
Open sets preserved in linear transformation that isn't bijective?
Hi, I'm not sure how else to phrase this.Let's say I have a linear transformation from R3 to R2. Let's assume in both spaces, I am using the standard topology with the standard euclidean distance metric. Does this mean that open sets in R3 will be mapped to open sets in R2 under this...- dumbQuestion
- Thread
- Linear Linear transformation Sets Transformation
- Replies: 5
- Forum: Topology and Analysis
-
M
Standard Matrix A for Linear Transformation T: R^3 to R^4
Linear transformation T:\,\mathbb{R}^3\,\to\,\mathbb{R}^4 Find the standard matrix A for T T\left(x_1,x_2,x_3\right)\,=\,\left(x_1 + x_2 + x_3, x_2 + x_3, 3x_1 + x_2, 2x_2 + x_3\right) \mathbf{v}\,=\,\begin{bmatrix} x_1\\ x_2\\ x_3...- mateomy
- Thread
- Linear Linear transformation Transformation
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
N
Vector & Tensor Transformation in Physics
I'm not sure if this belongs in physics or here. Consider the transformation of a vector from one coordinate system to the other. I can write: Vn = (∂yn/∂xm)Vm - contravariant form Vn = (∂xm/∂yn)Vm - covariant form In each case are the partials equivalent to the Jacobean matrices...- nigelscott
- Thread
- Physics Tensor Transformation Vector
- Replies: 2
- Forum: Calculus
-
A
Algorithm for a tensorial Karhunen-Loeve Transformation?
Does anyone happen to know a good algorithm for a numerical Karhunen-Loeve transformation for tensors? Specifically, I'm trying to solve for the eigentensors of a correlation bitensor, along the lines of \int_{-\infty}^{\infty} d^4x' \, C_{abc'd'}(x,x') \phi^{c'd'}(x') = \lambda \phi_{ab}(x)...- Aimless
- Thread
- Algorithm Transformation
- Replies: 3
- Forum: Set Theory, Logic, Probability, Statistics
-
I
Transformation function from ground state -> nth energy state, force applied, HO
Hello Everyone! I have a question regarding a Quantum problem I am trying to solve in L. Brown's Quantum Field Theory book, Chapter 1, Problem 4.f. Homework Statement I have a question which asks me to compute [p][/n], i.e. the probability that the ground state (n=0) is brought to the...- Imanbk
- Thread
- Applied Energy Force Force applied Function Ground Ground state State Transformation
- Replies: 3
- Forum: Advanced Physics Homework Help
-
U
How Do Non-Perpendicular Unit Vectors Affect Coordinate Transformation?
Homework Statement The x-y coordinates are being transformed into the u-v coordinates. Based on the diagram, u lies along x while v makes an angle α with x.The Attempt at a Solution The answer defined u and v weirdly.. Shouldn't x = u and y = v sin α ??- unscientific
- Thread
- Coordinates Transformation
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
W
Quantile function after Jacobian transformation
I am dealing with a random variable which is a transformation of another random variable of the form: Y:=aX^b+c The pdf of the random variable X is known and for the sake of example let it be exponential distribution or any other distribution with known and commonly available quantile...- WantToBeSmart
- Thread
- Function Jacobian Transformation
- Replies: 2
- Forum: Set Theory, Logic, Probability, Statistics
-
F
Finding the matrix for a linear transformation
Homework Statement Let V = Span{(1,1,0), (1,2,3)}. Define a linear transformation L: V => R^3 by L(1,1,0) = (1,0,0) and L(1,2,3) = (0,1,0). For any (x,y,z) element of V find L(x,y,z) Homework Equations The Attempt at a Solution It seems like there should be some straightforward...- Fractal20
- Thread
- Linear Linear transformation Matrix Transformation
- Replies: 26
- Forum: Calculus and Beyond Homework Help
-
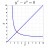
Transformation of variables in definite integral limits
Hello, I am going through Whittaker's treatise on Classical Mechanics. In chapter 3 he derives the equation of motion for a simple pendulum, and I have a question about his method. Starting from the general form for the equation of energy (s is the path): [SIZE="5"]\frac{m}{2}\dot{s}^2...- mfig
- Thread
- Definite integral Integral Limits Transformation Variables
- Replies: 13
- Forum: Classical Physics
-
H
Matrix transformation and inequality
Homework Statement Suppose U and V are unitary matrix, A and B are positive definite, Does: UAU-1 < VBV-1 implies A < B and vice versa?- hayu601
- Thread
- Inequality Matrix Transformation
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
L
Form of Lorentz Transformation Using West-Coast Metric
This is a fairly trivial question I think. I'm only asking it here because after some googling I was unable to find its answer. I was at one point led to believe that the form of the Lorentz-transformation matrix is dependent on the convention used for the Minkowski metric. Specifically it...- LittleSailor
- Thread
- Form Lorentz Lorentz transformation Metric Transformation
- Replies: 3
- Forum: Special and General Relativity
-
A
Lorentz velocity transformation problem
An observer on Earth observes two spacecraft moving in the same direction toward the Earth. Spacecraft A appears to have a speed of 0.50c, and spacecraft B appears to have a speed of 0.80c. What is the speed of spacecraft A measured by an observer in spacecraft B?So if S is the reference...- Aziza
- Thread
- Lorentz Transformation Velocity Velocity transformation
- Replies: 1
- Forum: Introductory Physics Homework Help
-
P
What is Lorentz transformation?
Iv been reading about general and special relativity and then I came across Lorentz transformation but I can't seem to find out what it is could you please help- pigman70
- Thread
- Lorentz Lorentz transformation Transformation
- Replies: 13
- Forum: Special and General Relativity
-
D
Does a Lagrangian preserving transformation obey the equations of motion?
This seems like such a simple question that I fully expect its solution to be embarrassingly easy, but try as I might I can't get the answer. Consider some system which can be described by N generalized coordinates q_1,...,q_N and a Lagrangian L(q_i,\dot{q}_i,t). (I'll just use q_i as a stand... -
J
Linear transformation and Change of Basis
Homework Statement Greetings, I have been stuck with this problem for a while, I thought maybe someone could give me some advice about it. Thanks a lot in advance. If T is a linear transformation that goes from R^2 to R^2 given that T(v1)= -2v2 -v1 and T(v2)=3v2. and B =...- Jimmy84
- Thread
- Basis Change Change of basis Linear Linear transformation Transformation
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
H
Understanding Lorentz Transformation of Spin 4-Vector
I have a problem understanding the Lorentz transformation of the spin. The spin 4-vector is defined in the rest frame of the particle as s^{\mu} = (0, \vec{s}) and then boosted in any other frame according to s'^{\mu} = (\gamma \vec{\beta} \cdot \vec{s}, \vec{s} +...- Heirot
- Thread
- 4-vector Lorentz Lorentz transformation Spin Transformation
- Replies: 17
- Forum: Special and General Relativity
-
P
Use the given transformation to evaluate the integral
∫∫10xy(dA), where R is the region in the first quadrant bounded by the lines y=x/2 and y=2x/3 and by the hyperbolas xy=1/2 and xy=3/2 The transformations given in the problem (these cannot be altered): x=u/v and y=v Relevant equations: The Jacobian - ∂(x,y)/∂(u,v) The attempt at a solution...- ptguard1
- Thread
- Integral Transformation
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
P
Image and kernel of iterated linear transformation intersect trivially
Homework Statement Given a linear transformation f:V -> V on a finite-dimensional vector space V, show that there is a postive integer m such that im(f^m) and ker(f^m) intersect trivially. Homework Equations The Attempt at a Solution Observe that the image and kernel of a linear...- pugnet
- Thread
- Image Kernel Linear Linear transformation Transformation
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
A
Entropy in an isobar transformation
What is the variation of entropy in an isobar transformation?- alialice
- Thread
- Entropy Transformation
- Replies: 2
- Forum: Thermodynamics
-
A
How Does the Bogoliubov Transformation Apply in BCS Theory with MFA?
Hello everybody, I am having some trouble to understand the significance behind the Bogoliubov transformation in the case of the BCS theory in the mean field approximation (MFA). Without going into all the details of the calculation the final result is a Bogoliubov transformation like: (1)...- arojo
- Thread
- Transformation
- Replies: 11
- Forum: Quantum Physics