Triple integrals Definition and 81 Threads

In mathematics (specifically multivariable calculus), a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z). Integrals of a function of two variables over a region in





R


2




{\displaystyle \mathbb {R} ^{2}}
(the real-number plane) are called double integrals, and integrals of a function of three variables over a region in





R


3




{\displaystyle \mathbb {R} ^{3}}
(real-number 3D space) are called triple integrals. For multiple integrals of a single-variable function, see the Cauchy formula for repeated integration.

View More On Wikipedia.org
Recent contents Top users
  1. WMDhamnekar

    Change in the order of integration in triple integrals

    If we solve the L.H.S. of this equation, we get ## \frac{(b-a)^3}{6}## and if we solve R.H.S. of this equation, we get ##-\frac{2b^3-3ba^2 +a^3}{6}## So, how can we say, this equation is valid? By the way, how can we use the hint given by the author here?
  2. A

    Where to use polar (cylindrical coor.) in double and triple integrals

    where the region of integration is the cube [0,1]x[0,1]x[0,1] my question is where can we use the polar coordinate? is it only usable if the region of integration looks like a circle regardless of the function inside the integral? (if yes it means that using this kind of transformation is wrong...
  3. karush

    MHB Triple Integral: $\dfrac{\sqrt{1-x^2}}{2(1+y)}$

    ok this is a snip from stewards v8 15.6 ex hopefully to do all 3 here $\displaystyle\int_0^1\int_{0}^{1}\int_{0}^{\sqrt{1-x^2}}\dfrac{z}{y+1} \,dxdzdy$ so going from the center out but there is no x in the integrand $\displaystyle\int_0^{\sqrt{1 - x^2}} \dfrac{z}{y + 1}dx =\dfrac{ \sqrt{1 -...
  4. karush

    MHB Explaining the Concept of Triple Integrals in Calculus

    15.6.4 Evaluate the iterated integral $$\int_0^1\int_y^{2y}\int_0^{x+y} 6xy\, dy\, dx\, dz$$OK this is an even problem # so no book answer but already ? by the xy
  5. W

    Probability Theory: Order statistics and triple integrals

    Homework Statement Let ##U_1, U_2, U_3## be independent uniform on ##[0,1]##. a) Find the joint density function of ##U_{(1)}, U_{(2)}, U_{(3)}##. b) The locations of three gas stations are independently and randomly placed along a mile of highway. What is the probability that no two gas...
  6. karush

    MHB 15.4.20 volumn via triple integrals

    $\textsf{The region in the first octant bounded by the coordinate planes and the surface }$ $$z=4-x^2-y$$ $\textit{From the given equation we get}$ \begin{align*}\displaystyle &0 \le z \le 4-x^2-y\\ &0 \le y \le 4-x^2\\ &0 \le x \le z \end{align*}...
  7. R

    MHB Spherical coordinates and triple integrals

    Suppose $\displaystyle f = e^{(x^2+y^2+z^2)^{3/2}}$. We want to find the integral of $f$ in the region $R = \left\{x \ge 0, y \ge 0, z \ge 0, x^2+y^2+z^2 \le 1\right\}$. Could someone tell me how we quickly determine that $R$ can be written as: $R = \left\{\theta \in [0, \pi/2], \phi \in [0...
  8. Draconifors

    Triple integral using cylindrical coordinates

    Homework Statement The first part of the question was to describe E the region within the sphere ##x^2 + y^2 + z^2 = 16## and above the paraboloid ##z=\frac{1}{6} (x^2+y^2)## using the three different coordinate systems. For cartesian, I found ##4* \int_{0}^{\sqrt{12}} \int_{0}^{12-x^2}...
  9. Anshul23

    Highschool graduate dealing with a triple integral?

    I recently came across a problem in Irodov which dealt with the gravitational field strength of a sphere. Took some time to get my head around it and figure how to frame a triple integral, but it felt good at the end. Am I going to start seeing triple integrals in the freshman year tho? If so...
  10. harpazo

    MHB Steps for Setting Up Triple Integrals

    I am really struggling setting up triple integrals. I need steps, simple steps normally applied when setting up integrals given a specific region.
  11. toforfiltum

    Integrating triple integral over region W

    Homework Statement $$f(x,y,z)=y$$ ; W is the region bounded by the plane ##x+y+z=2##, the cylinder ##x^2 +z^2=1##, and ##y=0##. Homework EquationsThe Attempt at a Solution Since there is a plane of ##y=0##, I decided that my inner integral will be ##y=0## and ##y=2-x-z##. But after this I have...
  12. TheSodesa

    Upper and lower bounds of a triple integral

    Homework Statement Let ##T \subset R^3## be a set delimited by the coordinate planes and the surfaces ##y = \sqrt{x}## and ##z = 1-y## in the first octant. Write the intgeral \iiint_T f(x,y,z)dV as iterated integrals in at least 3 different ways. Homework Equations \iiint_T f(x,y,z)dV =...
  13. kostoglotov

    Multiple Integral Challenge Question, I just need a hint

    Homework Statement I will just post an image of the problem and here's the link if the above is too small: http://i.imgur.com/JB6FEog.png?1Homework EquationsThe Attempt at a Solution I've been playing with it, but I can't figure out a good way to "grip" this problem. I can see some things...
  14. S

    Are These Triple Integrals Set Up Correctly?

    Are these correct? Thanks in advance! 1.) Set up the triple integral for ##f(x,y,z) = xy + 2xz## on the region ##0 ≤ x ≤4, 0 ≤ y ≤ 2## and ##0 ≤ x ≤ 3xy + 1##. ##\displaystyle \int_0^4 \int_0^2 \int_0^{3xy+1} 2y +2xz\ dz\ dy\ dx## \text{2.) Set up the triple integral in cylindrical...
  15. RJLiberator

    Center of Mass Using Triple Integrals Question

    Homework Statement My question is this: When finding center of mass, can you do so using spherical/cylindrical coordinates, or must you put it in cartesian coordinates? If you can use spherical/cylindrical coordinates, how do you set up the triple integrals ? Thank you. Homework...
  16. T

    Bounded regions and triple integrals

    Homework Statement a) sketch the region in the first octant bounded by the elliptic cylinder 2x^2+y^2=1 and the plane y+z=1. b) find the volume of this solid by triple integration. Homework EquationsThe Attempt at a Solution I have already sketched the elliptic cylinder and the plane. my...
  17. erzagildartz

    How to Integrate Triple Integrals in Different Coordinate Systems?

    how to solve triple integrals in cylindrical, spherical and rectangular coordinates ..easy ways
  18. B

    MHB Triple Integrals in Spherical Coordinates

    Hi all, I'm not sure how to get the boundaries in terms of both the spherical and cylindrical coordinates for this question. Here are the boundaries we were given in the solution. How was \frac{\pi}{4} for φ and \frac{1}{\sqrt{2}} for r obtained? Thanks!
  19. A

    Setting up triple integrals in different coordinates

    Homework Statement Assume that f(x,y,z) is a continuous function. Let U be the region inside the cone z=√x^2+y^2 for 2≤x≤7. Set up the intregal ∫f(x,y,z)dV over U using cartesian, spherical, and cylindrical coordinates. Homework Equations CYLINDRICAL COORDINATES x=rcosθ y=rsinθ z=z...
  20. A

    Does triple integrals have to have a specific interval?

    I hope this makes my question clear... suppose we have a triple integral of dzdydx for [0<x<1 , sqt(x)<y<1 , 0<z<1-y] and from the sketch we can see that 0<y<1 and 0<z<1... my question is this, if we change the integration to dzdxdy we get [0<x<y^2 , 0<y<1 , 0<z<1-y], is that the only way? or...
  21. G

    Volumes with triple integrals, aka I suck at geometry

    Homework Statement Calculate the volume of the body that is bounded by the planes: x+y-z = 0 y-z = 0 y+z = 0 x+y+z = 2 Homework Equations The Attempt at a Solution I made a variable substitution u = y+z v = y-z w = x which gave me the new boundaries u+w = 2...
  22. N

    Calculating Triple Integrals in Mathematica

    Homework Statement Evaluate ∫∫∫\sqrt{x^{2} + y^{2}} dA where R is the region bounded by the paraboloid y=x^2+z^2 and the plane y=4 Homework Equations I believe this is a problem where cylindrical coordinates would be useful 0 ≤ z ≤ \sqrt{4-x^2} 0 ≤ r ≤ 2 ( I think this is wrong). 0 ≤ θ ≤...
  23. M

    Finding Volume by use of Triple Integrals

    Homework Statement Find the Volume of the solid eclose by y=x^{2}+z^{2} and y=8-x^{2}-z^{2} The Attempt at a Solution Well know they're both elliptic paraboloids except one is flipped on the xz-plane and moved up 8 units. Knowing this, i equated the two equations and got...
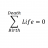
  24. STEMucator

    Setting up some triple integrals

    Homework Statement I want to know if I've gone about setting up these integrals in these questions properly before I evaluate them. (i). Find the mass of the cylinder S: 0 ≤ z ≤ h, x^2 + y^2 ≤ a^2 if the density at the point (x,y,z) is δ = 5z^4 + 6(x^2 - y^2)^2. (ii). Evaluate the...
  25. A

    Triple integrals, changing the order of integration

    Homework Statement Write out the triple integral for the volume of the solid shown in all six possible orders. Evaluate at least 2 of these integrals. Homework Equations I attached a picture of the figure. The front : x/2+z/5=1...
  26. T

    Differential Spherical Shells - Triple Integrals

    Homework Statement Despite the fact that this started as an extended AP Physics C problem, I turned it into a calc problem because I (sort of) can. If it needs to be moved please do so. There is a hollow solid sphere with inner radius b, outer radius a, and mass M. A particle of mass m...
  27. F

    Setting up Triple Integrals over a bounded region

    Homework Statement Set up triple integrals for the integral of f(x,y,z)=6+4y over the region in the first octant that is bounded by the cone z=(x^2+y^2), the cylinder x^2+y^2=1 and the coordinate planes in rectangular, cylindrical, and spherical coordinates. Homework Equations...
  28. N

    Regions of integration; bounds and triple integrals.

    Homework Statement My first problem is with 2ia) and 2ib), I got the correct answer, although not happy with my understanding of it. http://img826.imageshack.us/img826/1038/443pr.jpg The Attempt at a Solution (2ia and 2ib) The region that's of concern is the upper part between y = x^2 and...
  29. T

    Triple Integrals: Spherical Coordinates - Finding the Bounds for ρ

    Homework Statement Find the volume of the solid that lies above the cone z = root(x2 + y2) and below the sphere x2 + y2 + x2 = z. Homework Equations x2 + y2 + x2 = ρ2 The Attempt at a Solution The main issue I have with this question is finding what the boundary of integration is for ρ. I...
  30. T

    Triple Integrals: Finding Mass of a Bounded Solid

    Homework Statement Find the mass of a solid of constant density that is bounded by the parabolic cylinder x=y2 and the planes x=z, z=0, and x=1. The Attempt at a Solution https://dl.dropbox.com/u/64325990/Photobook/Photo%202012-06-07%202%2033%2024%20PM.jpg I first drew some diagrams to...
  31. R

    Measuring volume of spheres using triple integrals

    Homework Statement I'm just interested in knowing where the 4 comes from in front of the integral.
  32. T

    Finding Limits for Triple Integrals: How to Solve for the Intersection of Planes

    Homework Statement Use a triple integral to find the volume of the region. Below x+2y+2z=4, above z=2x, in the first octant. Homework Equations V=∫∫∫dV=∫∫∫dxdydz The Attempt at a Solution I have no clue where to begin as to finding those darn limits to integrate with. I'm sure...
  33. 1

    How to Calculate the Mass of a Pyramid Using Triple Integrals?

    Homework Statement Find the mass m of the pyramid with base in the plane z = 9 and sides formed by the three planes y = 0 and y - x = 5 and 6x + y + z = 28, if the density of the solid is given by δ(x,y,z) = y. Homework Equations The Attempt at a Solution This problem is driving...
  34. K

    Calculating volume using triple integrals

    Homework Statement Find the volume of the solid enclosed between the cylinder x2+y2=9 and planes z=1 and x+z=5Homework Equations V=∫∫∫dz dy dzThe Attempt at a Solution The problem I have here is setting the integration limits. I first tried using: z from 1 to 5-x y from √(9-x2) to -3 x from -3...
  35. M

    Integrating a Solid Enclosed by a Cylinder and Two Planes

    The solid enclosed by the cylinder x^2 + y^2 = 9 and the planes y + z = 5 and z=1. The biggest part for me (usually) is just being able to find my limits of integration for these problems (any suggestions about that would also be greatly appreciated). I think I found the correct limits for...
  36. D

    Triple Integrals with Cylindrical Coordinates

    Homework Statement Evaluate the integral, where E is the solid in the first octant that lies beneath the paraboloid z = 9 - x2 - y2. ∫∫∫(2(x^3+xy^2))dV Homework Equations x=rcosθ y=rsinθ x^2+y^2=r^2 The Attempt at a Solution θ=0 to 2π, r=0 to 3, z=0 to (9-r^2)...
  37. B

    Using Triple integrals to solve torque around a point.

    Homework Statement A cylindrical coffee cup (8 cm in diameter and 10 cm tall) is filled to the brim with coffee. Neglecting the weight of the cup, determine the torque at the handle (2 cm from edge of cup 5 cm up from bottom of cup). The easy way would be to just use the center of mass of the...
  38. M

    Questions about double and triple integrals

    Hey, I was just going through my vector calc textbook for this year and everything was going well until I reached double and triple integrals. My problem is the whole symmetry thing; when does (forgive me, I can't figure out the symbols) the integral from a to b become twice the integral from...
  39. D

    Vector Calc: Find the volume [using triple integrals]

    1. Find the volume, using triple integrals, of the region in the first octant beneath the plane 2x+3y+2z = 6 2. http://tutorial.math.lamar.edu/Classes/CalcIII/TripleIntegrals.aspx SOLUTION: 1. Assume X and Y are 0. Solve for Z: 2(0)+3(0)+2z=6 => z=3 (0,0,3) 2. Assume X...
  40. N

    What is the range for x in a triple integral for a wedge in the first octant?

    Write a triple integral to represent the volume of the solid The wedge in the first octant and from the cylinder y^2 + z^2 <= 1 by the planes y=x, x=0, z=0 First.. i find the range for z..; 0 <=z<= sqrt(1- y^2) then... i find the range for y..; let z =0 0<=y<=1 next, if i...
  41. L

    Another matlab question; triple integrals

    Homework Statement The question is to use MATLAB to evaluate a triple integral in spherical coordinates to find the mass density of the solid inside the cone z = (3x^2 + 3y^2)^.5 and below z = 5 where the mass density at (x,y,z) is equal to the z coordinate of the point. Homework...
  42. P

    How to Calculate Volume Using Triple Integrals for a Sphere and Planes?

    Homework Statement Use a triple integral to calculate the volume of the solid enclosed by the sphere x^2 + y^2 + z^2=4a^2 and the planes z=0 and z=a Homework Equations Transform to spherical coordinates (including the Jacobian) The Attempt at a Solution I'm stuck, as the radius...
  43. S

    Triple Integrals: Solving \int\int\int^{}_{B} ye^(-xy) dV

    Homework Statement \int\int\int^{}_{B} ye^(-xy) dV where B is the box determined by 0 \leq x \leq 4, 0 \leq y \leq 1, 0 \leq z \leq 5.Homework Equations The Attempt at a Solution \int^{4}_{0}\int^{1}_{0}\int^{5}_{0} ye^(-xy) dzdydx Integrating the first time I get zye-xy Plugging in 5 and 0 I...
  44. T

    Find centroid of region - triple integrals, please

    Homework Statement Find the centroid x,y,z of the region R cut out of the region 0<=z<=5sqrt(x2+y2) by the cylinder x2+y2=2x. Homework Equations x2+y2 = r2 x= rcosθ y= rsinθ The Attempt at a Solution Centroid x being Mx/m I'm guessing I've been working on this problem...
  45. S

    Change of variable in triple integrals

    Homework Statement Solve for the volume above the xy-plane and below the paraboloid z=1-x2/a2-y2/b2 I have gotten an answer that is close to the correct one, but I can't figure out where I am wrong. Homework Equations Solution: Volume is = ab\pi/2 The Attempt at a Solution...
  46. K

    Triple Integral: Volume Between Y=1-X & Y=Z^2-1

    Homework Statement Volume between Y=1-X and Y = Z^2 -1 The Attempt at a Solution http://img254.imageshack.us/img254/1743/42932830.jpg Uploaded with ImageShack.us Sorry, not a good drawer. 0 < y < 1 0< x < SqRoot: 1-y -1 < y < 0 0 < Z < Sqroot: 1 + y I'm not even sure...
  47. M

    Proving the shell method using triple integrals

    Homework Statement The volume of a solid of revolution using the shell method is \int_{a}^{b} 2\pi x f(x) dx. Prove that finding volumes by using triple integrals gives the same result. (Use cylindrical coordinates with the roles of y and z changed). Homework Equations dV = r dr d\theta...
  48. E

    Rewriting Triple Integrals: How to Split Up Limits for Cylindrical Surfaces?

    Homework Statement Rewrite this integral the other five ways \int_{x=0}^{1}\int_{z=0}^{1-x^2}\int_{y= 0}^{1-x} dydzdx Homework Equations Must be in rectangular coordinates The Attempt at a Solution 1.)\int_{z=0}^{1}\int_{x=0}^{\sqrt{1-z}}\int_{y= 0}^{1-x} dydxdz...
  49. D

    Moment of inertia with triple integrals

    so i have to find the moment of inertia of a solid cone given by the equations z = ar and z = b by using a triple integral. The density of the cone is assumed to be 1. so the integral looks like ∫ ∫ ∫ r^2 dV. so first i did it with dV = rdrdθdz with limits r (from 0 to z/a), θ (from 0 to 2pi)...
  50. R

    Triple Integrals: Finding Limits Without Sketching

    Homework Statement Here is a solved problem: [PLAIN]http://img3.imageshack.us/img3/6948/97765276.gif In part (e), they formulated the triple integral using the limits of integration they found by sketching the region. Is there a way we can find the limits of integration without...
Back
Top