You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Wave function Definition and 878 Threads
-
C
If you measure the energy of a system how does wave function collapse
Hey. Given that if you measure the energy of a wave function, the wave function must collapse to the eigenstate corresponding to the eigenvalue measured. Does that mean when you measure the energy of a wave function it must collapse the wave function into one of these stationary states...- cooev769
- Thread
- Replies: 12
- Forum: Quantum Physics
-
M
Wave function of two different fermions
Hi! According to quantum field theory, must the wave function of two different fermions be antisymmetric? If I have a state of two equal fermions: b^\dagger(p_1)b^\dagger(p_2)|0> I can construct the general state of two fermions: \int d^3p_1 d^3p_2f(p_1,p_2)b^\dagger(p_1)b^\dagger(p_2)|0>...- Marchigno
- Thread
- Replies: 1
- Forum: Quantum Physics
-
E
Normalizing a wave function and finding probability density
Homework Statement A state of a particle bounded by infinite potential walls at x=0 and x=L is described by a wave function \psi = 1\phi_1 + 2\phi_2 where \phi_i are the stationary states. a) Normalize the wave function. b) What is the probability to find the particle between x=L/4 and...- Emspak
- Thread
- Replies: 2
- Forum: Introductory Physics Homework Help
-

Time Dependent Wave Function for Particle in Infinite Square Well
Homework Statement A particle is in a bound state of the infinite square well. It is in a state represented by the following wavefunction, written here at t=0: ψ(x)= -√(2/3)√(2/L) * sin (3πx/L) + i*√(1/3)√(2/L) * sin (2πx/L) (a)Write the full time-dependent wavefunction for this state...- LunaFly
- Thread
- Replies: 2
- Forum: Advanced Physics Homework Help
-
C
Permenance of Collapsed Wave Function Spin State
Hello Everyone, General curiosity question. We start with a particle who is in superposition. We observe it and collapse its wave function. This is how the particle's spin is determined. Two states can exist, spin up or spin down. My question is, once we observe the spin state, is...- ChiralWaltz
- Thread
-
- Tags
- Function Spin State Wave Wave function
- Replies: 6
- Forum: Quantum Physics
-
S
Wave function in infinite square well, with potential step
Homework Statement A Particle energy A trapped in infinite square well. U(x)=0 for 0<x<L and U(x)=U0 for L<x<2L. find the wave function of the particle when A) E>U0 B) E<U0 C) E=U0. Homework Equations 1-D time independent Schrodinger equation. The Attempt at a Solution I have...- slasakai
- Thread
- Replies: 1
- Forum: Introductory Physics Homework Help
-
E
Normalizing a wave function and calculating probability of position
Forgive me if this goes in elementary physics, but I think since it's an upper level undergrad class Homework Statement A state of a particle bounded by infinite potential walls at x=0 and x=L is described by a wave function \psi = 1\phi_1 + 2\phi_2 where \phi_i are the stationary states. a)...- Emspak
- Thread
- Replies: 2
- Forum: Advanced Physics Homework Help
-
R
Determine the wave function of the particle
Homework Statement A particle coming from +∞ with energy E colides with a potential of the form: V = ∞ , x<0 (III) V = -V0 , 0<x<a (II) V = 0, x>a (I) a) Determine the wave function of the particle considering that the amplitude of the incident wave is A. Writting the amplitude of the...- rmfw
- Thread
- Replies: 4
- Forum: Advanced Physics Homework Help
-

Wave Function Terminology - Are these synonyms?
Are the quantum mechanical terms "probability amplitude" and "probability density" used interchangeably?- shanepitts
- Thread
- Replies: 4
- Forum: Quantum Physics
-
A
Wave function (schrodinger equation)
Homework Statement Sketch the wave function ψ(x) corresponding to a particle with energy E in the potential well shown below. Show correctly relative values of amplitude and wavelength in different regions. Homework Equations none? The Attempt at a Solution I guess I was a bit...- asdf12312
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
L
Is it possible for a wave function to have a discontinuous first derivative?
Wave function and its first derivative must be continuous becaus wave function is solution of Schroedinger equation: Let's examine one dimensional case. ## \frac{d^2 \psi(x)}{dx^2}+V(x)\psi(x)=E\psi(x) ## David J. Griffiths gives a problem in his quantum mechanics book...- LagrangeEuler
- Thread
- Replies: 14
- Forum: Quantum Physics
-
L
Phonons: For oscillator wave function
For oscillator wave function ##\frac{1}{\sqrt 2}(y-\frac{d}{dy})\psi_n(y)=\sqrt{n+1}\psi_{n+1}(y)## ##\frac{1}{\sqrt 2}(y+\frac{d}{dy})\psi_n(y)=\sqrt{n}\psi_{n-1}(y)## and I interpretate ##n## as number of phonons. Of course ##\psi_n(y)=C_ne^{-\frac{y^2}{2}}H_n(y)##. And ##C_n=f(n)##...- LagrangeEuler
- Thread
- Replies: 12
- Forum: Quantum Physics
-
I
Changing the Hamiltonian without affecting the wave function
How many ways can we change the Hamiltonian without affecting the wave functions (eigenvectors) of it. Like multiply all the elements in the matrix by a constant. I'm facing a very difficult Hamiltonian,:cry: I want to simplify it, so the wave function will be much easier to derive. Thanks in...- Isaac.Wang88
- Thread
- Replies: 1
- Forum: Quantum Physics
-
R
Wave Function for 1000 Particles in a Box
Homework Statement At the instant t=0, there's a system with 1000 particles in a box of length a. It is known that 100 have energy 4E1 and 900 have energy 225E1, where E1 is the energy of the fundamental state. i) Build a wave function that can represent the state of a particle ii) How many...- rmfw
- Thread
- Replies: 6
- Forum: Advanced Physics Homework Help
-
N
How can the normalization of a wave function be achieved?
Homework Statement A quantum mechanical wavefunction for a particle of mass m moving in one dimension where α and A are constants. Normalize the function - that is find a value of A for which \int^{\infty}_{-\infty}|ψ|^2dx=1 Homework Equations ψ(x,t)= |Ae^{-α(x^2 + it\hbar/m)}|^2...- Numnum
- Thread
-
- Tags
- Function Wave Wave function
- Replies: 6
- Forum: Advanced Physics Homework Help
-
I
Time independent wave function vs the initial wave function
I thought there was a difference, but I'm being told now that the time independent wave function is the wave function at t=0- iScience
- Thread
- Replies: 1
- Forum: Quantum Physics
-
S
Wave function simplification in relativistic coordinates?
My textbook says ψ(x,t)=exp(i(p_{0}x^{0} + p^{→}\cdotx^{→})/h)=exp(i*p\cdotx/h) (note that by h I mean 'h-bar'...couldn't find the symbol). I don't recognize (like my text implies I should) how the first equation equals the second. Where did the p_{0}x^{0} go? Sorry for my stupidity here. Any...- sciencegem
- Thread
- Replies: 4
- Forum: Quantum Physics
-

Asymptotic properties of Hydrogen atom wave function
I am working through an explanation of the wave function of the Hydrogen atom. I have got as far as deriving the version of Schrodinger's equation for the one-dimensional problem in which only the radial coordinate can vary: ##[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial^2...- andrewkirk
- Thread
- Replies: 3
- Forum: Quantum Physics
-
W
Why People Rarely Discuss the Wave Function of Anyons - Explained
it seems that people never talk about the wave function of a few anyons why? i guess the reason is that if they consider the wave function, then they will only get bosons or fermions they cannot get anyons from a wave function In other words, there is no such thing like a wave...- wdlang
- Thread
-
- Tags
- Function Wave Wave function
- Replies: 2
- Forum: Quantum Physics
-
F
Question about wave function and 1 dimensional well
Homework Statement Present is a wavefunction of a particle in a 1-dimensional well. Choose the correct potential that could result in this wave function: Homework Equations See belowThe Attempt at a Solution I want to make sure I am analyzing this correctly. I think the correct answer here...- fredrogers3
- Thread
-
- Tags
- Function Wave Wave function
- Replies: 1
- Forum: Advanced Physics Homework Help
-
A
Wave Function Sketch for Particle at Rest with Given Potential and Energy
Homework Statement Given the potential, and energy of a particle at rest, Sketch the wave function Homework Equations The time invariant schroedinger equation The Attempt at a Solution I don't really know how to do this question Basically, I am given the potential...- allenh98
- Thread
- Replies: 1
- Forum: Introductory Physics Homework Help
-
L
Wave function in Infinite/Finite Potential Wells
Homework Statement What is the functional form of the wave function in the ground state in the five regions x<0, 0<x<a, a<x<b, b<x<L, and x>L? I've attached the picture of the potential well as well here: Homework Equations Schrodinger time independent equation The Attempt at a...- lee_sarah76
- Thread
- Replies: 10
- Forum: Advanced Physics Homework Help
-
A
Wave function orthogonal components
1. The photon wave function, an EM wave, has orthogonal electric and magnetic components. I have gathered the impression that the electron wave function has only one. Is this correct? 2. By analogy with EM waves, can the electron's spin rate be identified with the frequency of its wave...- Alfred Cann
- Thread
- Replies: 7
- Forum: Quantum Physics
-
S
Position variables in the wave function
I would like some clarification as to the mathematical and physical definitions of the position variables in the wave function. I often see that it is treated as a variable independent of time; this is utilized in the separation of variables technique. However, the Schrodinger equation implies...- SheikYerbouti
- Thread
- Replies: 1
- Forum: Quantum Physics
-
Z
Express wave function in spherical harmonics
1. Problem: I have a wave function ψ(r) = (x + y + z)*f(r) and want to find the expectation values of L2 and Lz. It is suggested that I first change the wave function to spherical coordinates, then put that in terms of spherical harmonics of the form Yl,m. 2. Homework Equations ...- z2394
- Thread
- Replies: 4
- Forum: Advanced Physics Homework Help
-
H
Vertex Function & Wave Function of Mesons: Exploring Their Relation
I need to know the relation of wave function and vertex function of mesons. Any one give me an explanation of them. Are they same? in some journals their expressions are the same and in other papers the wave function expresses as a function of the vertex function of meson. Which one is the...- Hluf
- Thread
- Replies: 3
- Forum: High Energy, Nuclear, Particle Physics
-
W
Problem with normalization wave function position/momentum space
Homework Statement We start with a pure state at t=0 of an electron is C e^{- a^2 x^2} \left(\begin{array}{c} 1\\ i \end{array}\right) Probability density of measuring momentun p_0 and third component of spin - \frac{\hbar}{2} And probability of measuring a state with momentum...- WarDieS
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
L
Integration help with normalizing wave function
Homework Statement ψ(x,t) = Ae-λxe-iwt Normalize this and solve for AHomework Equations [tex]\int_{-∞}^{∞}|ψ|2dx = 1The Attempt at a Solution I got to A2\int_{-∞}^{∞}e^{-2λx}dx The solution manual multiplies it by 2 and only goes from 0 to ∞ instead of from -∞ to ∞. I'm trying to do it from...- leroyjenkens
- Thread
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
C
Linear combination of wave function of a Hydrogen Atom
Homework Statement I am given a linear combination of wave function of HYDROGEN ATOM Ψ=1/2(Ψ200 +Ψ310+Ψ311+Ψ31-1), where the subscripts are n, l, m respectively. I was asked to find all the possible outcomes when measuring Lx and their corresponding probabilities. Homework Equations...- czng71
- Thread
- Replies: 6
- Forum: Advanced Physics Homework Help
-
A
How to find the wave function using WKB?
I would like to understand how to find wave functions using WKB. Homework Statement Given an electron, say, in the nuclear potential $$U(r)=\begin{cases} & -U_{0} \;\;\;\;\;\;\text{ if } r < r_{0} \\ & k/r \;\;\;\;\;\;\;\;\text{ if } r > r_{0} \end{cases}$$ With the barrier region given...- a1111
- Thread
-
- Tags
- Function Wave Wave function Wkb
- Replies: 1
- Forum: Advanced Physics Homework Help
-
N
Does position operator have eigen wave function?
I am learning quantum mechics. The hypothesis is: In the quantum mechanics, all operators representing observables are Hermitian, and their eigen functions constitute complete systems. For a system in a state described by wave function ψ(x,t), a measurement of observable F is certain to...- nosafeway
- Thread
- Replies: 5
- Forum: Quantum Physics
-
C
The Wave Function Of The Universe
This may be a bizarre question, but if the entire universe has a wave function, and wave function collapse for real (unlike in Bohmian mechanics or the Many Worlds interpretation), then what caused the collapse of the wave function of the universe? It must have been collapsed before we came...- Crazy4Physics
- Thread
- Replies: 31
- Forum: Quantum Physics
-
R
How to show a wave function satisfies the shrodinger eqn
Homework Statement If a state is a linear combination of two energy eigenstates, does its wavefunction satisfy the time independent shrodinger equation? I guess in general, how would I show if the wavefunctions of a state does or does not satisfy the time-independent schrodinger equation...- richyw
- Thread
-
- Tags
- Function Wave Wave function
- Replies: 19
- Forum: Introductory Physics Homework Help
-
S
Hydrogen wave function in terms of m_z after m_y measurement
Homework Statement Given the following wave function for hydrogen: psi(r, t=0) = (1/sqrt(10))*(2*psi_100 - psi_210 + sqrt(2)*psi_211 + sqrt(3)*psi_21(-1)) where the subscripts show n, l, m_z, respectively, and the psi_nlm_z are already normalized. - At t=0, we measure and find l = 1...- sapphire_glow
- Thread
- Replies: 1
- Forum: Advanced Physics Homework Help
-
F
Does the environment cause wave function collapse
I came across this statement by bhobba in another thread and it got me to thinking, if the "environment" itself is capable of collapsing the wave function, then how is it possible to produce an interference pattern in a double slit experiment? After all, the particle isn't traveling through a...- Fiziqs
- Thread
- Replies: 94
- Forum: Quantum Physics
-
T
Why does the wave function have to collapse upon measurement?
How does the Copenhagen interpretation motivate its claim that the wave function of a quantum system collapses when a property of the system is being measured? I mean, was there some problem they were trying to solve by introducing the notion of wave function collapse? What would happen if the...- TriKri
- Thread
- Replies: 6
- Forum: Quantum Physics
-

What is the v(p) polynomial in radial wave function
I think the solution to the radial schrodinger equation includes a form of the Laguerre polynomials, the polynomial v(ρ). Does anyone know what this v(ρ) polynomial is called? The only information my book gives is: "The polynomial v(ρ) is a function well known to applied mathematicians."...- lonewolf219
- Thread
- Replies: 2
- Forum: Quantum Physics
-
J
The angular momentum operator acting on a wave function
Hi guys, I need help on interpreting this solution. Let me have two wave functions: \phi_1 = N_1(r) (x+iy) \phi_2 = N_2(r) (x-iy) If the angular momentum acts on both of them, the result will be: L_z \phi_1 = \hbar \phi_1 L_z \phi_2 = -\hbar \phi_2 My concern is, \phi_1 and \phi_2...- Jerrynap
- Thread
- Replies: 4
- Forum: Quantum Physics
-

Vaxjo Interpretation of Wave Function
For those interested in this stuff, what is your opinion of this less well-known Vaxjo interpretation: Vaxjo Interpretation of Wave Function: 2012 http://arxiv.org/pdf/1210.2390.pdf "Einsteins Dream”-Quantum Mechanics as Theory of Classical Random Fields http://arxiv.org/pdf/1204.5172.pdf...- bohm2
- Thread
- Replies: 1
- Forum: Quantum Interpretations and Foundations
-
M
Is the wave function real or abstract statistics?
Is the wave function describing reality or does it describe the observers uncertainty about the system? I say that it's real but I would like to hear any comments or evidence that suggest the wave function isn't a description that has a one to one correspondence with a underlying reality. It's...- matrixrising
- Thread
- Replies: 118
- Forum: Quantum Physics
-

Quantum mechanics: Find the wave function given the conditions
Homework Statement Consider a 1-dimensional linear harmonic oscilator. Any measurement of it's energy can either return the value of ħw/2 or 3ħw/2, with equal probability. The mean value of the momentum <P> at the instant t=0 is <P> = (mħw/2)1/2 Find the wave function ψ(x,0) for this...- Jalo
- Thread
- Replies: 7
- Forum: Advanced Physics Homework Help
-
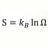
Has Wave Function Collapse Been Verified Experimentally ?
In QM theory entangled particles or photons are in superposition for spin (spin up or spin down) or for polarization angles. When one of the space like separated pair is measured for a spin or polarization observable, the wave function collapses and the other particle is then in a...- morrobay
- Thread
- Replies: 1
- Forum: Quantum Physics
-
H
How do I normalize the wave function Are^{-r/\alpha} from r=0 to r=\infty?
Homework Statement Normalize the wave function Are^{-r/\alpha} from r=0 to r=\infty where A and \alpha are constants. The Attempt at a Solution Beware, this is my first actual normalization problem! This thread could turn out to be pointless! I started by integrating the function...- Hertz
- Thread
-
- Tags
- Function Wave Wave function
- Replies: 12
- Forum: Advanced Physics Homework Help
-
S
Find the wave function of a Gaussian wave packet
In particular, i am solving part b. I pulled off a couple of formulas from a textbook, but I'm quite sure they are incorrect to apply here. Can anyone guide me? Below is my attempt.- serverxeon
- Thread
- Replies: 4
- Forum: Advanced Physics Homework Help
-
M
Need a refresher on finding probabilities of a wave function.
After a few months off (yay summer/internships), I'm 'back in the saddle' and I'm trying to catch up with my Q-mech. I have a wave function which is given as a particle sliding freely on a circular wire: \Psi = A(1 + 4cos\phi) I need to find the corresponding probabilities. So I know that I...- mateomy
- Thread
- Replies: 4
- Forum: Advanced Physics Homework Help
-
S
How Do You Determine the Correct Wave Function in a Quantum Square Well?
Homework Statement Assume a free particle, V=0, in a infinite potential square well between -L/2 and L/2 solve for the wave function for this particle. Homework Equations Time independent schrodinger equationThe Attempt at a Solution After arriving at the second order differential equation...- serverxeon
- Thread
-
- Tags
- Function Wave Wave function
- Replies: 5
- Forum: Advanced Physics Homework Help
-
L
Wave function and infinite square well potential
Homework Statement An electron in a one-dimensional infinite square well potential of length L is in a quantum superposition given by ψ = aψ1+bψ2, where ψ1 corresponds to the n = 1 state, ψ2 corresponds to the n = 2 state, and a and b are constants. (a) If a = 1/3, use the normalization...- leroyjenkens
- Thread
- Replies: 9
- Forum: Introductory Physics Homework Help
-
F
Normalising a wave function to dirac's delta
Hi guys! There is something I fail to understand in normalising wave functions to dirac's delta. Let's take the free particle solution as an example. Please note that my question is not about using the solution as much as about undestanding the concept. ----- The situation The general...- ffia
- Thread
-
- Tags
- Delta Function Wave Wave function
- Replies: 1
- Forum: Advanced Physics Homework Help
-
C
Why Does the 3s Hydrogen Wave Function Use the Polynomial (27-18σ+2σ²)?
Hi, I am wondering why the associated Laguerre Polynomial for the 3s hydrogen wave function is (27-18σ+2σ2). My physical chemistry book tells me that the complete hydrogen wave function is given by: \Psi(r,\theta,\phi)= RnlY^{m}_{l}(\theta,\phi) and Rnl(r) uses the Laguerre polynomial...- chrisa88
- Thread
- Replies: 7
- Forum: Quantum Physics
-
H
Full reflection of wave function for E = V0
I have seen discussions which suggests that there is no solution for the interval after the step in a step potential where E = V0. The set up is a potential step where E = V0, with an interval 1 defined as x < 0 before the step and an interval 2 as x > 0 after the step. Is the following...- hnicholls
- Thread
- Replies: 1
- Forum: Quantum Physics