A glitch in Jorrie’s Cosmo-Calculator?

[JimJCW]

TL;DR Summary

Recently I noticed that when calculating Dnow and Dthen using Jorrie’s calculator, the result is slightly inconsistent with those obtained from Gnedin’s or Wright’s calculator. Could there be a glitch in Jorrie’s calculator?

Jorrie’s LightCone7-2017-02-08 Cosmo-Calculator can be very useful and handy when making calculations based on the ΛCDM model. Recently I noticed that when calculating D_now and D_then using Jorrie’s calculator, the result is slightly, but persistently, inconsistent with those obtained from Gnedin’s or Wright’s calculator. An example is shown below:

The inconsistency becomes more obvious for small z values. For example,

Based on the observation that the results from Gnedin’s and Wright’s calculators are consistent with each other, and that Jorrie’s result shown in the above figure is peculiar for small z values, one may wonder whether there is a glitch in Jorrie’s calculator. You can help by doing the following:

(1) Verify that there is such a peculiar result in Jorrie’s program and​

(2) Contact @Jorrie about it if you know how.​

​

 

[Vanadium 50]

This is why relying on other people's calculations if you can't do them yourself is a bad idea.

 

[JimJCW]

This is why relying on other people's calculations if you can't do them yourself is a bad idea.

How would you fix the glitch, assuming there is one in Jorrie’s calculator?

 

[jim mcnamara]

Hmm. @Jorrie would probably like to look at this problem.

 

[Vanadium 50]

How would you fix the glitch

First I'd have to find it.

 

[kimbyd]

Knowing how these calculations are done, chances are it's an issue with the numerical integration. It would make sense if Jorrie used a less-good approximation for that integral, causing this result. The behavior at low-z suggests, to me, that using a fixed delta-z for the integral might be the culprit.

 

[robphy]

By looking at the sources of the webpages
(and, in some cases, the list of .js files called as scripts),
one can find the underlying calculations of these three resources.

As @Vanadium 50 suggests, it probably would be good to be able to obtain the results from one's own calculation. I think it makes it easier to order to understand what others have done... and possibly identify different approaches that may lead to the discrepancies that you note.

 

[Jorrie]

Hmm. @Jorrie would probably like to look at this problem.

Hmm, yes will do. Perhaps good to note that this calculator was more of an educational tool than an attempt at a quasi-professional tool.

 

[Jorrie]

Hmm, yes will do. Perhaps good to note that this calculator was more of an educational tool than an attempt at a quasi-professional tool.

It seems that in the process of evolving the calculator so that the 'future', i.e. "negative redshifts" could be visible, the distance parameters got out of step with the redshift parameter by a small amount. I will have to investigate deeper to fix.

 

[JimJCW]

It seems that in the process of evolving the calculator so that the 'future', i.e. "negative redshifts" could be visible, the distance parameters got out of step with the redshift parameter by a small amount. I will have to investigate deeper to fix.
View attachment 301053

Using the 2021 version of the calculator, I get a different result:

Note that D_then is in Gly.

 

[Jorrie]

Using the 2021 version of the calculator, I get a different result:
Note that D_then is in Gly.

Apart from the anomalous shift to the right, taking into account the Gly/Gpc distance scaling, it is only the single data point at the origin that is different between the two graphs. The latter is an easily fixable error. The shift to the right is more troublesome, due to the way that the algorithm was implemented, requiring somewhat of a reprogramming. Will hopefully get around to it soon.

I think these anomalies were not noticed before, because for larger redshifts they disappear in the noise. Cool that you have spotted them. :-))

 

[robphy]

Summary:: Recently I noticed that when calculating Dnow and Dthen using Jorrie’s calculator, the result is slightly inconsistent with those obtained from Gnedin’s or Wright’s calculator. Could there be a glitch in Jorrie’s calculator?

Jorrie’s LightCone7-2017-02-08 Cosmo-Calculator

...actually links to the 2021 version:
http://jorrie.epizy.com/Lightcone7-2021-03-12/LightCone_Ho7.html .
Here is the 2017 version
http://jorrie.epizy.com/LightCone7-2017-02-08/LightCone_Ho7.html .

 

[robphy]

(I'm not actively working in this...
I was just curious about the question
and was poking around...)

From a diff (using https://www.diffchecker.com/diff )
of the two calculation files, there are two differences.

One in Calculate()
if (s > 0.9999999 && s < 1.0000001) { z = 0; // the 'now' line, force z to zero } else { z = s - 1; // redshift } s=z + 1 // ensure they are in step H = s * qa * Ho;
The "s=z+1" (line 236) is new in the 2021 version.

The other in ScaleResults().
Line 357 has a revised value
var ConversionHo = 978
which was 973.1 in the 2017 version.

(My remarks in #7 still apply.)

 

[JimJCW]

...actually links to the 2021 version:
http://jorrie.epizy.com/Lightcone7-2021-03-12/LightCone_Ho7.html .
Here is the 2017 version
http://jorrie.epizy.com/LightCone7-2017-02-08/LightCone_Ho7.html .

You are right; Jorrie’s LightCone7-2017-02-08 Cosmo-Calculator ...actually links to the 2021 version: http://jorrie.epizy.com/Lightcone7-2021-03-12/LightCone_Ho7.html. That was my mistake; I meant to say, “Jorrie’s LightCone7-2021-03-12 Cosmo-Calculator”.

Jorrie changed the 2017 version to the 2021 version to fix the discrepancy in the Hubble parameter calculation. See the thread, Discrepancy in Jorrie’s LightCone7-2017-02-08 Cosmo-Calculator.

 

[JimJCW]

Apart from the anomalous shift to the right, taking into account the Gly/Gpc distance scaling, it is only the single data point at the origin that is different between the two graphs. The latter is an easily fixable error. The shift to the right is more troublesome, due to the way that the algorithm was implemented, requiring somewhat of a reprogramming. Will hopefully get around to it soon.

I did some experiments with the calculator and noticed the following:

If we change the ‘number of fine grain steps’ and ‘fine grain steps’ in the Calculation.js file from

N = 10000000​

sf = 0.00001​

to

N = 1000000000​

sf = 0.000001​

We can get the following result:

While this reduces the effect of the glitch, the glitch is not completely eliminated (see the following result for smaller z):

Does this suggest anything?

 

[Jorrie]

... While this reduces the effect of the glitch, the glitch is not completely eliminated (see the following result for smaller z):
Does this suggest anything?

Yup, tightening the integration loops always helps, but it slows things down quite a bit. It was more of a problem when the calculator was first prototyped (around 2009), so I guess one can now insert your values for the faster computers of today.
However, the factor 100 tightening of the loops just reduces the error for the very low z by a factor 100, so it does not fix the real problem in the implementation. I'm still looking at that.

The problem with 'funnel' shape around the origin is easy to fix, at least temporarily, by taking out the statements in lines 241-245,
if (Math.abs(a-1) < 0.0001)
{
Dnow = 0;
Dthen = 0;
}
which forces Dnow and Dthen to zero for a very close to 1 (i.e, 'now').
The issue should disappear when the 'asymmetry problem' is fixed.

 

[JimJCW]

The problem with 'funnel' shape around the origin is easy to fix, at least temporarily, by taking out the statements in lines 241-245,
if (Math.abs(a-1) < 0.0001)
{
Dnow = 0;
Dthen = 0;
}
which forces Dnow and Dthen to zero for a very close to 1 (i.e, 'now').

You are right; if I do the following:

if (Math.abs(a-1) < 0.000001)​

// if (Math.abs(a-1) < 0.0001)​

{​

Dnow = 0;​

Dthen = 0;​

}​

I get this:

 

[Jorrie]

Cool!
A little bit of background on the (convoluted path of the) development of Lightcone7. It really started all the way back in 2007, after a thread: https://www.physicsforums.com/threads/cosmo-calculator-recession-speed-tutorial.163996/ by the late and much appreciated Marcus.

Later in the thread, member hellfire confirmed a link to his own super-efficient, single pass calculator (post #18). With his permission, I started to use it in efforts of my own. Unfortunately @hellfire has not been seen around since 2010 and AFIAK, his original calculator is no longer accessible.

That "humble calculator" (@hellfire's words) has since grown to a multi-pass, much more generalized tool, but that efficient single pass code/module, although not very easy to read, is still used multiple times in Lightcone7. Marcus played a huge role in guiding the development, as a sort-off community project. Other members also played significant roles and to some extent, it became a 'camel', a "horse designed by a committee"! In a way, this community project is still continuing...

Since personal (and other) websites come and go, maybe we should find a more permanent place for it to reside?

 

[Jorrie]

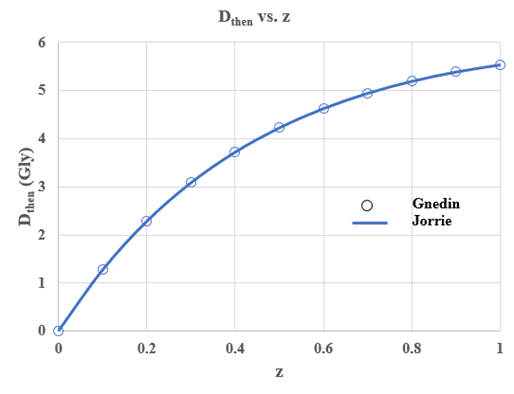
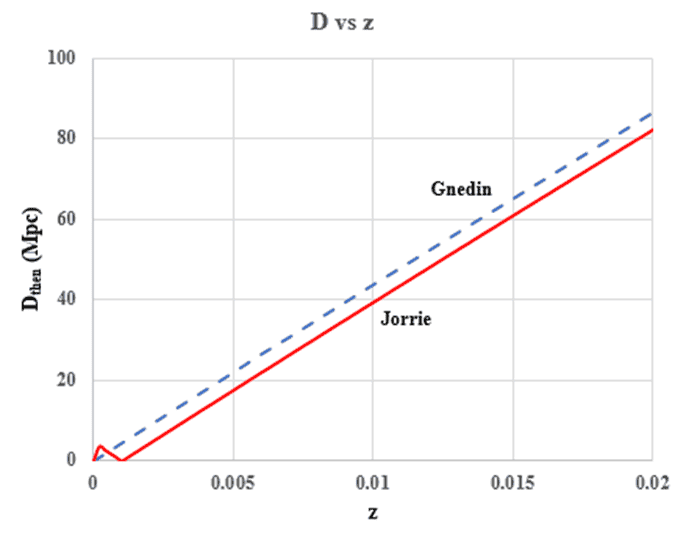
While I got nostalgic, I looked around on a backup and I found @hellfire's 2009 Calculate Function that I later incorporated into Lightcone7. For what it's worth, here it is:

function Calculate(OmegaM, OmegaR, OmegaL, HubbleP, zo, Omegat)
{
// >>>>>> Latest update 12-05-2009
// >>>>>> Original: http://www.geocities.com/alschairn/cc_e.htm

// >>>>>> input

var Ol = OmegaL * 1; // Lambda density par
var Or = OmegaR * 1; // Radiation density par
var Om = OmegaM * 1; // matter density par
var Ok = 1 - Om - Or - Ol; //curvature densioty par
var H = HubbleP * 1; // Hubble const now
var zt = zo * 1; // redshift of object
var at = (1 / (1 + zt)); // requested redshift value

// >>>>>> output
var T = 0; // time
var Dc = 0; // comoving distance
var Dp = 0; // proper distance
var Da = 0; // angular diameter distance
var Dl = 0; // luminosity distance
var Hp = 0; // time variable Hubble constant
var Omt = 0;
var Olt = 0;
var Ort = 0;

// >>>>>> auxiliary
var N = 100000;
var a = 0;
var a_ic = 0;
var qa = 0;
var pa = 1 / N; // Incremental a
var Eset = 0;
var Dtc = 0;
var Dtp = 0;

// >>>>>> conversion 1/H to Myr
var Tyr = 978000;

// >>>>>> Loop from a = 0 to a = 1, stop to get at values
while (a_ic < 1)
{
a = a_ic + (pa / 2); // expansion factor as incremented
qa = Math.sqrt((Om / a) + Ok + (Or / (a * a)) + (Ol * a * a)); // time variable density function (Or input 10000 times hi)
T = T + (pa / qa); // time (age)
Dc = Dc + ((1 / (a * qa)) * pa); // proper distance now
Dp = Dp + ((1 / qa) * pa); // proper distance then
a_ic = a_ic + pa; // new a
if ((a > at) && (Eset == 0))
{
window.document.cc_e.Epoch.value = Math.round((T * (Tyr / H)) * 10000) / 10000;
Dtc = Dc;
Dtp = Dp;
Dtl = Dl;
Dta = Da;
Eset = 1;
};
}

// >>>>>> auxiliary
Okc = Ok;

// >>>>>> Angular diameter distance -- D. Hogg, astro-ph/9905116
if ((Math.abs(Okc)) < 0.05)
{
Da = at * (Dc - Dtc);
}
else if (Okc > 0)
{
Da = at * (1/Math.sqrt(Okc)) * 0.5 * (Math.exp(Math.sqrt(Okc) * (Dc - Dtc)) - Math.exp(- Math.sqrt(Okc) * (Dc - Dtc)));
}
else
{
Okc = - Okc;
Da = at * (1/Math.sqrt(Okc)) * Math.sin(Math.sqrt(Okc) * (Dc - Dtc));
}

if (Da < 0)
{
Da = - Da;
}

// >>>>>> Luminosity distance
Dl = Da / (at * at);

// >>>>>> Conversion
T = T * (Tyr / H);
Dc = Dc * (Tyr / H);
Dtc = Dtc * (Tyr / H);
Dp = Dp * (Tyr / H);
Dtp = Dtp * (Tyr / H);
Da = Da * (Tyr / H);
Dl = Dl * (Tyr / H);

// >>>>>> Output "now"
window.document.cc_e.Age.value = Math.round(T * 10000) / 10000;
window.document.cc_e.Size.value = Math.round(Dc * 10000) / 10000;
window.document.cc_e.Dcomoving.value = Math.round((Dc - Dtc) * 10000) / 10000;
window.document.cc_e.Dproper.value = Math.round((Dp - Dtp) * 10000) / 10000;
window.document.cc_e.Dluminosity.value = Math.round(Dl * 10) / 10;
window.document.cc_e.Dangular.value = Math.round(Da * 10000) / 10000;
//window.document.cc_e.Vrec.value = Math.round((1-at*at) / (1+at*at)*10000)/10000; //temp Vrec calc using normal Doppler
window.document.cc_e.Vrec.value = Math.round(((((Dc - Dtc) / 3.26) * H) / 300000) * 10000) / 10000;

// >>>>>> Hubble parameter then, at a = at
Hp = (1/at) * H * Math.sqrt((Om * (1/at)) + (Or * (1/(at * at))) + (Ok) + (Ol * at * at));

// >>>>>> Omegas
Omt = (Om * (H * H) / (Hp * Hp * at * at * at));
Olt = (Ol * (H * H) / (Hp * Hp));
Ort = (Or * (H * H) / (Hp * Hp * at * at * at * at));
// >>>Ot = (Omt + Olt + Ort);
Ot = 0.0001878754 * Hp * Hp;
//Ot = Ot + ""
//Ot = Ot.substring(0,4)
//parseFloat(Ot)

// >>>>>> auxiliary
Okc = 1 - Omt - Olt - Ort;

// >>>>>> Output "then"
window.document.cc_e.Hthen.value = Math.round(Hp * 10000) / 10000;
window.document.cc_e.Dthen.value = Math.round((Dc - Dtc) * at * 10000) / 10000;
window.document.cc_e.Vrecthen.value = Math.round(((((Dc - Dtc) * at / 3.26) * Hp) / 300000) * 10000) / 10000;
window.document.cc_e.Sizethen.value = Math.round(Dtc * 10000) / 10000;
window.document.cc_e.OmegaMt.value = Math.round(Omt * 10000000) / 10000000;
window.document.cc_e.OmegaLt.value = Math.round(Olt * 10000000) / 10000000;
window.document.cc_e.OmegaRt.value = Math.round(Ort * 10000000) / 10000000;
window.document.cc_e.Omegat.value = Math.round(Ot * 10000000) / 10000000;
// window.document.cc_e.Omegat.value = Ot;
}

 

[Ibix]

Since personal (and other) websites come and go, maybe we should find a more permanent place for it to reside?

You could put the code to github? I expect github won't last forever (nothing does), but it has a huge amount of inertia. Your code wouldn't run there, but it would always be available for someone to host should your version disappear.

 

[robphy]

While I got nostalgic, I looked around on a backup and I found @hellfire's 2009 Calculate Function that I later incorporated into Lightcone7. For what it's worth, here it is:

Great.
Here is the archived webpage
http://web.archive.org/web/2008*/http://www.geocities.com/alschairn/cc_e.htm

While the snapshots have form-interface, the .js script (presumably what you posted above) wasn't archived.
Here's one snapshot
http://web.archive.org/web/20080813234529/http://www.geocities.com/alschairn/cc_e.htm

For posterity, someone could piece it together.

If the code were text on a webpage (as opposed to just being a script), archive.org might have archived it.

This thread was captured a few days ago.
If it captures it again, then it will capture the code you posted as text.
https://web.archive.org/web/2022050...a-glitch-in-jorries-cosmo-calculator.1014779/

 

[Jorrie]

Thanks robphy, I will look into the github option.

 

[robphy]

Thanks robphy, I will look into the github option.

Just to clarify:
The github idea was due to @Ibix .
I just found the webpage [without its working script] on archive.org.

 

[Jorrie]

Thanks to you both, and also to JimJCW for the heads up.
If any of you are interested in participating in modifying, testing and ironing out of bugs in Lightcone7, it will be great.

I'm still pondering the solution to the proper-distance/redhift offset problem encountered, which is suppressed by tightening of the integration loops, but not completely removed.

Perhaps a community project can take it to the next level of "amateur professionalism".

 

[Ibix]

If any of you are interested in participating in modifying, testing and ironing out of bugs in Lightcone7, it will be great.

Sounds interesting - happy to help.

 

[Jorrie]

Thanks! Will let you know when I pick up the ropes again - still puzzling about a better way to economically implement the standard model's equations, in order to eliminate irritating offsets, like the one this thread is about.

 

[JimJCW]

- still puzzling about a better way to economically implement the standard model's equations, in order to eliminate irritating offsets, like the one this thread is about.

I have been playing with Line 248 of the Calculation.js file:

Dnow = Math.abs(Dtc-Dc);​

Here is my result:

I don’t understand what is going on, but hope you can see something interesting here.

 

[Jorrie]

One should not need to put correcting offsets into that subtraction The problem arises because both De and Dtc are the result of a massive integration loops and at z=0, they do not agree (they should be equal and they are not). I think it is differences in round-off errors in the two loops that causes it.

Essentially, Lightcone's z can run from near "positive infinite" to near "negative infinite". I think it will be better to start at zero and work towards the two extremes,, but this may case other issues.

I'm slowly working towards such a solution, and I may ask you guys to help with testing.

 

[JimJCW]

One should not need to put correcting offsets into that subtraction The problem arises because both De and Dtc are the result of a massive integration loops and at z=0, they do not agree (they should be equal and they are not). I think it is differences in round-off errors in the two loops that causes it.

Essentially, Lightcone's z can run from near "positive infinite" to near "negative infinite". I think it will be better to start at zero and work towards the two extremes,, but this may case other issues.

I'm slowly working towards such a solution, and I may ask you guys to help with testing.

I think that makes sense. I can help with testing.

 

[Jorrie]

Here is a patched version of Lightcone7, dated 2002-05-14, which numerically corrects for the offset in the low-z regime.
When testing in that regime, remember to set z_lower and z_upper in the input boxes to a range compatible with the z-regime of interest. When simply run over the default range of z, it produces too course an output for proper testing.

There are still anomalies around z=0, but it is good to remember that the homogeneity condition required by LCDM does not hold for z < 0.025 or so, roughly the value for the Como cluster.

I leave the old link in my signature for now, in-case you want to compare. Still pondering an overhaul of the legacy-ridden calculation.js module.

 

[JimJCW]

Here is a patched version of Lightcone7, dated 2002-05-14, which numerically corrects for the offset in the low-z regime.
When testing in that regime, remember to set z_lower and z_upper in the input boxes to a range compatible with the z-regime of interest. When simply run over the default range of z, it produces too course an output for proper testing.

There are still anomalies around z=0, but it is good to remember that the homogeneity condition required by LCDM does not hold for z < 0.025 or so, roughly the value for the Como cluster.

I leave the old link in my signature for now, in-case you want to compare. Still pondering an overhaul of the legacy-ridden calculation.js module.

I will look at it tonight. I noticed the following:

When specifying the following:

I got this:

The ranges of z values seem not consistent.

 

[Ibix]

Hi @Jorrie. I've spent a peaceful afternoon reading your Insights on how this works and looking through the Javascript before implementing it in python using one of its canned integration routines to do the hard work. I've uncovered a couple of possible issues that you might want to look at.

First I looked at your Lightcone7 Tutorial Part III to try to understand the maths you were implementing. I noticed a minor bug in that article - it defines $\Omega_r=\Omega_r/S_{eq}$, which I think ought to be $\Omega_m/S_{eq}$, or possibly even $\Omega_mS/S_{eq}$.

But between that page and the Javascript I was able to write a python program to replicate the outputs. There's no UI - "inputs" are just variables and you need to specify all the $z$ values manually and the result comes out as a file. The code is below and should just work as long as you have the scipy.integrate package installed, which is what does the numerical work. It's partially commented - see the Insight linked above and Lightcone7 itself for details of what's actually being calculated.

import math, scipy.integrate

##########################################################################
# Various constants
rhoConst = 1.7885e+9  # 3 / (8 pi G)
secInGy = 3.1536e+16  # s / Gyr
tempNow = 2.725       # CMB temperature now
Hconv = 1 / 978       # Convert km/s/Mpc -> Gyr^-1
infty = float("inf")  # Infinity - used as a limit in integrator

##########################################################################
# Inputs (Planck 2015, copied from Jorrie's calculator
H0 = 67.74                # H0 control
OmegaL = 0.691            # OmegaL control
Omega = 1                 # Omega control
z_eq = 3370               # z_eq control
zvals = [ 1089.999,       # The z values copied from Lightcone7's table
          339.0316542,
          104.9771906,
          32.02928913,
          9.293570928,
          2.207515378,
          0,
          -0.6893293728,
          -0.8690917659,
          -0.9451725312,
          -0.9773721629,
          -0.991 ]

##########################################################################
# Constants derived from inputs
H0 *= Hconv                                    # H0 in Gyr^-1
rhocritNow = rhoConst * (H0 / secInGy)**2      # Critical density now
s_eq = 1 + z_eq                                # Stretch when OmegaM=OmegaR
OmegaM = (Omega - OmegaL) * s_eq / (s_eq + 1)  # Energy density of matter
OmegaR = OmegaM / s_eq                         # Energy density of radiation
OmegaK = 1 - OmegaM - OmegaR - OmegaL          # Curvature energy density

##########################################################################
# Functions
def H(s):
    """Hubble constant as a function of stretch, s = 1/a, where a is the
    usual FLRW scale factor"""
    return H0 * math.sqrt(OmegaL
                            + OmegaK * s**2
                            + OmegaM * s**3
                            + OmegaR * s**4)
def TH(s):
    return 1 / H(s)
def THs(s):
    return TH(s) / s
def formatted(vals):
    """Convenience function to apply standard formatting to a bunch of
    numbers"""
    return ",".join(("%7.2e" % v) for v in vals)

##########################################################################
# For each specified z, calculate all the things Jorrie's calculator does
# and output them as CSV for easy pasting into a spreadsheet
with open("planck.csv","w") as op:
    op.write("z,Scale (a),S,Tnow Gyr,R Gly,Dnow Gly,Dthen Gly," \
                +"DHor Gly,Dpar Gly,Vgen/c,Vnow/c,Vthen/c,H(z)," \
                +"Temp (K),rho kg/m3,OmegaM,OmegaL,OmegaR,OmegaT\n")
    for z in zvals:
        s = 1 + z
        #s = 1.001 + z  # Uncomment to replicate a systematic bug in Lightcone7
        a = 1 / s
        Tnow = scipy.integrate.quad(THs, s, infty)[0]
        R = 1 / H(s)
        Dnow = abs(scipy.integrate.quad(TH, 1, s)[0])
        Dthen = Dnow / s
        Dhor = scipy.integrate.quad(TH, 0, s)[0] / s
        Dpar = scipy.integrate.quad(TH, s, infty)[0] / s
        Vgen = H(s) / (H0 * s)
        Vnow = Dnow * H0
        Vthen = Dthen * H(s)
        Temp = tempNow * s
        rhocrit = rhoConst * (H(s) / secInGy)**2
        OmegaMT = (Omega-OmegaL) * s**3 * (H0 / H(s))**2
        OmegaLT = (H0 / H(s))**2 * OmegaL
        OmegaRT = OmegaMT * s / s_eq
        OmegaTT = OmegaMT + OmegaLT + OmegaRT
        op.write(formatted([z, a, s, Tnow, R,
                            Dnow, Dthen, Dhor, Dpar,
                            Vgen, Vnow, Vthen,
                            H(s) / Hconv,
                            Temp, rhocrit,
                            OmegaMT, OmegaLT, OmegaRT, OmegaTT])+"\n")

If you run this it should produce a table of data in a CSV file called Planck.csv that should open in a spreadsheet package. It produces all of the columns Lightcone7 does in the same order and to Lightcone7's default precision, to make it easy to compare with the Javascript results. I uncovered two issues by doing this, working with your 2022-05-14 version.

I think the first issue is what's causing the bug that @JimJCW is seeing. Your $S$ actually appears to be $1.001+z$ across the board. Since everything calculates from $S$ the only practical effect of this is that the $z$ being used in the calculation is off by 0.001 compared to the results, which looks to be about right for where the graphs posted on page 1 are hitting the horizontal axis.

There's a line commented out in the loop at the end of my code that switches to defining $S=1.001+z$ and almost all of the (fairly slight) differences between python and Javascript results go away if you uncomment that. The remainder are, I think, rounding disagreements.

The second issue is that I can't get my Dpar and Dhor values to match yours. According to your Insight, $$\begin{eqnarray*}
D_{par}&=&\frac 1S\int_{s=S}^\infty T_Hds\\
D_{hor}&=&\frac 1S\int_{s=0}^S T_Hds
\end{eqnarray*}$$and that's fairly simple to implement, so I don't think I've made a mistake there. Given those definitions, I'd expect $(D_{par}+D_{hor})S=\int_0^\infty T_Hds=\mathrm{const}$, and that's true of my results but is not true in the Lightcone7. So I think there might be something wrong either in those calculations or the definition in the Insight. I haven't investigated further - not even going and looking up those formulae in a textbook.

I have had a quick look at the Javascript backing this, and I would say it could probably be simplified quite a lot. It looks like it's been through quite a few re-writes but could probably do with another one focussed on cleaning it up a bit. Happy to help with that if you like - I have some ideas, but I don't want to trample on your toes.

 

[Jorrie]

Hi @Jorrie. ...

I have had a quick look at the Javascript backing this, and I would say it could probably be simplified quite a lot. It looks like it's been through quite a few re-writes but could probably do with another one focussed on cleaning it up a bit. Happy to help with that if you like - I have some ideas, but I don't want to trample on your toes.

Hi Ibix, thanks a ton! Yes, part of that Js code dates back to 2010 and comes from @Hellfire's original. Didn't want to fix what was working, but it has been added to so many times that it is quite a mess by now. I tried to get too much mileage out of that old engine...
I think both the distance and horizon anamolies originate there.

I would prefer to leave the overall Input/Output structure the same, but the calculation module to be completely redesigned and cleared up to produce the required outputs. I would be grateful if you want to assist - and it looks like you already have a working algorithm!

And yes, it should be $\Omega_r=\Omega_m/S_{eq}$. Will fix that, if I can figure out how to edit that old tutorial...

 

[Jorrie]

Hi @Jorrie.
...
The second issue is that I can't get my Dpar and Dhor values to match yours. According to your Insight, $$\begin{eqnarray*}
D_{par}&=&\frac 1S\int_{s=S}^\infty T_Hds\\
D_{hor}&=&\frac 1S\int_{s=0}^S T_Hds
\end{eqnarray*}$$and that's fairly simple to implement, so I don't think I've made a mistake there. Given those definitions, I'd expect $(D_{par}+D_{hor})S=\int_0^\infty T_Hds=\mathrm{const}$, and that's true of my results but is not true in the Lightcone7. So I think there might be something wrong either in those calculations or the definition in the Insight. I haven't investigated further - not even going and looking up those formulae in a textbook.

I have used Tamara Davis' "Fundamental Aspects of the Expansion of the The universe and Cosmic Horizons" equations in the Tutorial, but the implementation in Lightcone7 was a bit different and quite possibly inaccurate.

Note that $(D_{par}+D_{hor})S=\int_0^\infty T_Hds=\mathrm{const}$ only holds for comoving distances and not for the proper distances used in Lightcone7, where $D_{par}$ tends to infinity and $D_{hor}$ tends to a finite constant value. This is clear from the Davis Three-panel Cosmological Expansion graphs in my sig.

 

[JimJCW]

I think the first issue is what's causing the bug that @JimJCW is seeing. Your $S$ actually appears to be $1.001+z$ across the board. Since everything calculates from $S$ the only practical effect of this is that the $z$ being used in the calculation is off by 0.001 compared to the results, which looks to be about right for where the graphs posted on page 1 are hitting the horizontal axis.

Please let me know the line number and file name concerning the '1.001 + z' problem.