- #106
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
A perfectly stiff wheel cannot roll on a stiff floor?
- I
- Thread starter andrewkirk
- Start date
-
- Tags
- Roll Rolling motion Stiffness Wheel
- Featured
In summary, the conversation discusses the concept of rolling motion, specifically the commencement of rolling motion. It is mentioned that a wheel's axis of rotation is through the instantaneous point of contact with the ground, not through its axle. It is then proposed that a necessary condition for the commencement of rolling is either that the wheel is not a perfect circle or that the ground deforms under the weight of the wheel. The problem is solved by replacing the circular wheel with a regular polygon, allowing the wheel to pivot around the grounded vertex closest to the forward direction of the applied force. It is also suggested that a wheel's shape can be a circle with a portion of the bottom part chopped off, creating a flat contact region that allows rolling. The conversation also
Physics news on Phys.org
- #107
DaveC426913
Gold Member
- 22,989
- 6,664
Cool.
No, they will not roll.
The thread, the radii and the two touch-points of the wheels together form a trapezoid.
The first thing that rolling would theoretically result in is the lengthening of the longest side (the line between the two touch-points).
That trapezoid cannot be deformed and still maintain symmetry.
Not so sure now.
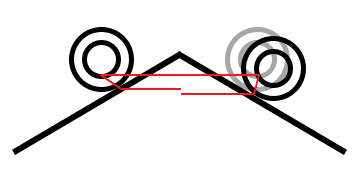
The thread, the radii and the two touch-points of the wheels together form a trapezoid.
The first thing that rolling would theoretically result in is the lengthening of the longest side (the line between the two touch-points).
That trapezoid cannot be deformed and still maintain symmetry.
Not so sure now.
Attachments
Last edited:
- #108
- 42,084
- 10,187
Well, it does depend on the relationship between the ratio of the radii and the angle of the slope. What if the slope increases to 60 degrees?DaveC426913 said:Cool.
No, they will not roll.
The thread, the radii and the two touch-points of the wheels together form a trapezoid.
The first thing that rolling would theoretically result in is the lengthening of the longest side (the line between the two touch-points).
That trapezoid cannot be deformed and still maintain symmetry.
- #109
- 15,078
- 8,437
To elaborate, static equilibrium is maintained when the torque due to gravity and the torque due to the tension in the string are in opposite directions. The former is non-zero as long as ##\theta < 90^o##. The latter becomes zero when the radius of the inner wheel is large enough so that the position vector from the contact point to the point of application of the tension is horizontal. This happens when ##r/R=\cos\theta##. For ##r/R>\cos\theta## the two torques are in the same direction and there can be no equilibrium. Note: Torques are calculated using the point of contact of the wheel with the incline as origin.haruspex said:Well, it does depend on the relationship between the ratio of the radii and the angle of the slope. What if the slope increases to 60 degrees?
- #110
Baluncore
Science Advisor
2023 Award
- 15,556
- 9,307
The distance between circle centres is the length of tight string.
It is not the change in height, Sin(30°), but the change in horizontal separation, Cos(30°) that is important.
They will not roll because R/2R = 0.5 string released, is less than Cos(30°) = 0.886 string required between centres.
Roll becomes possible when Cos(slope) = R/2R = 0.5 which will be when the slope becomes > 60°.
It is not the change in height, Sin(30°), but the change in horizontal separation, Cos(30°) that is important.
They will not roll because R/2R = 0.5 string released, is less than Cos(30°) = 0.886 string required between centres.
Roll becomes possible when Cos(slope) = R/2R = 0.5 which will be when the slope becomes > 60°.
- #111
A.T.
Science Advisor
- 12,554
- 3,687
DaveC426913 said:Cool.
No, they will not roll.
The thread, the radii and the two touch-points of the wheels together form a trapezoid.
The first thing that rolling would theoretically result in is the lengthening of the longest side (the line between the two touch-points).
That trapezoid cannot be deformed and still maintain symmetry.
Not so sure now.
View attachment 223687
It boils down to whether to string goes above or below the contact points.
- #112
A.T.
Science Advisor
- 12,554
- 3,687
DaveC426913 said:Cool.
Can this spool roll down the incline without slipping, as the problem statement suggests?
Found here:
http://www.chegg.com/homework-help/questions-and-answers/spool-move-spool-rests-top-incline-made-two-uniform-disks-radius-r-mass-m-connected-horizo-q24458961
Attachments
- #113
Baluncore
Science Advisor
2023 Award
- 15,556
- 9,307
No. But that is not a genuine solvable problem. It is an advertisement for “advanced physics tutors”. It is designed to disempower and confuse students to the point where they subscribe to a study program. Now being advertised on PF.A.T. said:Can this spool roll down the incline without slipping, as the problem statement suggests?
- #114
jmolmo
- 6
- 2
But, if I pull the string upwards...? Will it roll?A.T. said:Can this spool roll down the incline without slipping, as the problem statement suggests?
View attachment 223703
Found here:
http://www.chegg.com/homework-help/questions-and-answers/spool-move-spool-rests-top-incline-made-two-uniform-disks-radius-r-mass-m-connected-horizo-q24458961
- #115
jmolmo
- 6
- 2
You're right ... In a rigid body, you can't consider 2 simultaneous "centers of rotation" at the same time (so, a point from which all the other body points motion can be described as circles around that "point")... such body would be no rigid.andrewkirk said:I promised some pictures earlier, and I've finally made them. Here are three pictures, showing a wheel rotating around a point of contact with the ground. The first is a perfectly circular wheel, the second is a wheel with the bottom flattened (eg a tyre compressing under the weight of the load) and the third is a polygon.
We see that, if the wheel rotates around the foremost point of contact in the direction of travel (marked) through a non-zero angle, it all works OK for the polygon and the flattened wheel, but not for the perfect circle, which has to go below the floor.
The answer arrived at in the thread above is that there is no rotation through any angle about that point. Rather, the statement that the wheel is rotating about that point is just a description of the instantaneous relative velocities of points on the wheel.
View attachment 215189 View attachment 215190 View attachment 215191
The only way you can describe the movement of the points of a wheel if the geometrical lowest point of the wheel is moving along a line, is as the composition of one translation movement that follows that "line", and one rotational movement around the center of the wheel. So, or that "center of rotation" is constantly flipping between the center of the wheel and the geometrical contact point (but never both at the same time), or there's no point in saying that the contact point has been the center of rotation at any time, even if an infinitesimal time is considered.
Last edited:
- #116
Baluncore
Science Advisor
2023 Award
- 15,556
- 9,307
Define upwards, and what you mean by pull. Consuming string at the fixed anchor point will move the spool up the ramp. Feeding string out from the fixed anchor point will allow the spool to roll. Raising the anchor point to change the angle between the string and the slope will make a big difference at some point.jmolmo said:But, if I pull the string upwards...? Will it roll?
- #117
jmolmo
- 6
- 2
If it's an string, I think it's clear what I mean by pull. If you mean how much pull, then image you do very, very little at first (0.01N) ... and then more and more.Baluncore said:Define upwards, and what you mean by pull. Consuming string at the fixed anchor point will move the spool up the ramp. Feeding string out from the fixed anchor point will allow the spool to roll. Raising the anchor point to change the angle between the string and the slope will make a big difference at some point.
Similar threads
- Replies
- 7
- Views
- 493
- Replies
- 4
- Views
- 793
- Replies
- 7
- Views
- 3K
- Replies
- 8
- Views
- 2K
- Replies
- 22
- Views
- 2K
- Replies
- 16
- Views
- 8K
- Replies
- 3
- Views
- 2K
- Replies
- 20
- Views
- 1K
- Replies
- 10
- Views
- 4K
- Replies
- 10
- Views
- 2K
Share:

