A popular explanation of Bell's inequalities

[Spathi]

TL;DR Summary

In one book on quantum mechanics, I found a very simple analogy to Bell's inequalities; I liked this analogy, but I am not sure it is correct in general.

In one book on quantum mechanics, I found a very simple analogy to Bell's inequalities, which explains their essence without delving into the details of the physical experiment. I liked this analogy, but it seems the authors got it a little confused, so I ask for clarification if it is correct in general.

I suppose the authors described the CHSH inequalities, but the explanation in Wikipedia is too short to understand. Here is the description of the mentioned analogy from the book:

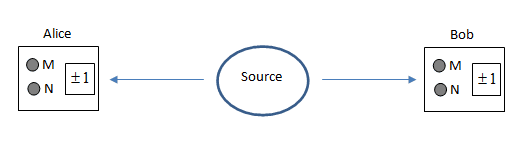
Each of the two remote observers - Alice and Bob - uses a device that has two buttons, labeled M and N, and a screen that can show either +1 or -1. During the experiment, Alice and Bob are unable to communicate with each other.

The source located roughly halfway between Alice and Bob sends them a couple of particles of some kind. Alice and Bob receive these particles and each insert them into their device. Then they select a random button on the device and press it at the same time. Each device displays a value of +1 or -1, possibly related to the state of the generated particle. The entire operation described is called an event.

Both observers keep a record of the buttons they pressed and the numbers displayed. After receiving data on a large array of numbers, both parties meet and perform a correlation analysis of their records. Specifically, they estimate the value

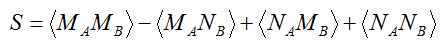
Here, Ma, Mb, Na, Nb are the numbers that Alice and Bob receive after pressing the corresponding buttons. Each event only contributes to one of the values MaMb, MaNb, NaMb, NaNb. The book says that if | S | is greater than 2, then Bell's inequalities are violated.

This is how, if I understand it correctly, a typical experiment looks like:

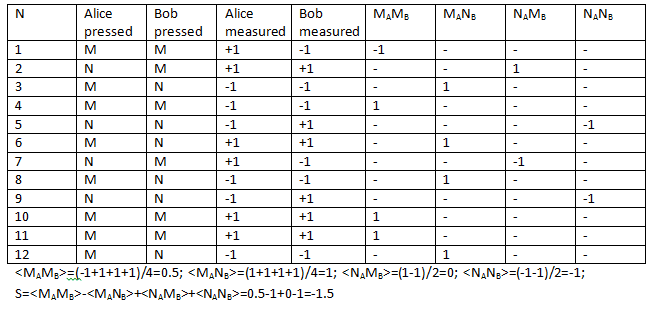
I wrote a program that counts S for different algorithms of generating measurements of Alice and Bob. The following conclusions were obtained. Suppose Alice and Bob's buttons are completely random; Alice's measurement is also completely random, and Bob's measurement depends on Alice's measurement, but does not depend on the button that Alice and Bob pressed. Then S can take values from -2 to 2 (after averaging a large number of events).

Now suppose Alice's measurement is random, and Bob's measurement is defined as follows: if Alice pressed M and Bob pressed N, Bob's measurement is opposite to Alice's, otherwise Bob's measurement is the same as Alice's. Then S equals 4 - this is a violation of Bell's inequalities.

This leads to very interesting conclusions, but only under the condition that this whole analogy is correct. For the latter algorithm (for which S = 4) Bob's measurement indirectly depends on Alice's button, but does not correlate with it; therefore, Alice cannot convey information to Bob by pressing the button for a reason. This is consistent with what I have read in various sources about quantum entanglement - it does not allow information to be transmitted, but at the same time it cannot be called a complete absence of any interaction. Einstein called it “spooky action at distance”, and this characteristic is understandable, since particles located at different times can be entangled, so “spooky action through time” is an equivalent formulation.

Please comment on whether this analogy is correct in general. Another question: if we switch from this analogy to a real experiment with photon polarizabilities, what will Alice's button, Bob's button, Alice's measurement, Bob's measurement correspond to? Is that correct that pressing the buttons by Alice or Bob corresponds to the process of the measurement, and the values of Alice or Bob to the result of that measurement?

 

[Killtech]

Now suppose Alice's measurement is random, and Bob's measurement is defined as follows: if Alice pressed M and Bob pressed N, Bob's measurement is opposite to Alice's, otherwise Bob's measurement is the same as Alice's. Then S equals 4 - this is a violation of Bell's inequalities.

There is nothing particularly special about a S=4 result if one allows Bob to have a dependence on Alice. Bell's inequalities are build on the premise that there is no such dependence.

 

[Spathi]

There is nothing particularly special about a S=4 result if one allows Bob to have a dependence on Alice. Bell's inequalities are build on the premise that there is no such dependence.

In the case of the described model, if Bob's measurement does not depend in any way on Alice's button, |S| will be no more than two.
Doesn't quantum entanglement imply the mutual dependence of two particles? This is what Einstein called “spooky action at distance”.

 

[StevieTNZ]

In one book on quantum mechanics,

It is probably helpful if you give us the title and author(s) of the book from which this comes.

 

[PeroK]

In the case of the described model, if Bob's measurement does not depend in any way on Alice's button, |S| will be no more than two.
Doesn't quantum entanglement imply the mutual dependence of two particles? This is what Einstein called “spooky action at distance”.

I'll tell you what else is "spooky action": that the ghost of Einstein still haunts modern QM.

In terms of what you posted, I don't immediately see the analogy with quantum entanglement.

 

[Spathi]

It is probably helpful if you give us the title and author(s) of the book from which this comes.

This was a Russian version of the book "Quantum physics: an introduction based on photons" by A. Lvovsky.

 

[DrChinese]

Doesn't quantum entanglement imply the mutual dependence of two particles? This is what Einstein called “spooky action at distance”.

The two entangled particles form a system of two quantum particles with spatio-temporal extent. Their evolution cannot be considered as being separate and independent. This is called "quantum nonlocality", which is a more modern and common term for "spooky action at a distance". However, it is not clear that there is actually "nonlocal" action, as there are viable quantum interpretations that lack that feature.

In your example, it matters what the M and N measurements are. Some settings will not lead to a violation of a Bell inequality. Clearly, when Alice and Bob measure the same thing, there will be a perfect correlation. That's not an issue in the Bell scenario, as EPR-type local realistic theories predict the same. It's when there are certain differences in the settings that Bell is relevant.

 

[Spathi]

I'll tell you what else is "spooky action": that the ghost of Einstein still haunts modern QM.

Richard Feynman said that nobody understands the quantum mechanics. You think he was wrong?

In terms of what you posted, I don't immediately see the analogy with quantum entanglement.

On two other forums, some people wrote me that this analogy is correct. You claim that they are wrong?

 

[vanhees71]

This quote by Feynman in my opinion refers only to philosophical matters. From a physical point of view QT is the most comprehensive theory we have. It encompasses all of physics except the quantum theory of the gravitational interaction. Thus from a physical point of view that's the only thing that is not understood.

 

[PeroK]

On two other forums, some people wrote me that this analogy is correct. You claim that they are wrong?

Analogy is in the eye of the beholder!

 

[DrChinese]

On two other forums, some people wrote me that this analogy is correct. You claim that they are wrong?

As mentioned, it matters what angles M and N are set at. You then plug in the quantum expectation statistics:

Matches=sin^2 (Alice's angle - Bob's angle) [for entangled photons, per your example]

When Alice=60 degrees and Bob=0 degrees, the expectation is .75 matches.
When Alice=60 degrees and Bob=30 degrees, the expectation is .25 matches.
When Alice=60 degrees and Bob=60 degrees, the expectation is 0 matches.
Etc.

Proceed from there to get the total quantum prediction (using your 4 permutations). You haven't done that, so your example is incomplete. Your S value won't be meaningful of anything otherwise. You also need to understand the reason why 2 is the local realistic upper limit, and why it conflicts with the quantum prediction. That has a maximum value of about 2.82 on best case setup, although experiments usually show 2.3 or so.

The CHSH inequality is relatively more advanced than other analogies. Trying to model it without an understanding of everything involved is inevitably going to confuse your simulation. I would recommend looking at Mermin's:

https://csiflabs.cs.ucdavis.edu/~gusfield/mermin_moon_Bell's_inequalities.pdf

Or even at my own example:

http://drchinese.com/David/Bell_Theorem_Easy_Math.htm

 

[gentzen]

Richard Feynman said that nobody understands the quantum mechanics. You think he was wrong?

That quote is from Feynman's 1964 Cornell Messenger lectures. Bell's inequality first appeared in Bell's groundbreaking 1964 paper, "On the Einstein Podolsky Rosen paradox". The much cited paper "Proposed experiment to test local hidden-variable theories" by Clauser, Horne, Shimony, and Holt appeared in 1969. It seems fair to say that you should not claim to understand quantum mechanics if you have not yet learned the lessons of those papers.

 

[Spathi]

That quote is from Feynman's 1964 Cornell Messenger lectures. Bell's inequality first appeared in Bell's groundbreaking 1964 paper, "On the Einstein Podolsky Rosen paradox". The much cited paper "Proposed experiment to test local hidden-variable theories" by Clauser, Horne, Shimony, and Holt appeared in 1969. It seems fair to say that you should not claim to understand quantum mechanics if you have not yet learned the lessons of those papers.

You mean that if Feynman knew the Bell's theorem, he wouldn't say this quote? But Bell only improved the EPR paradox, the "spooky action at distance" was understood by Einstein before Feynman.

 

[PeroK]

You mean that if Feynman knew the Bell's theorem, he wouldn't say this quote? But Bell only improved the EPR paradox, the "spooky action at distance" was understood by Einstein before Feynman.

Science isn't dependent on the words of the great men (and women) taken as gospel. In fact, in one of his Messenger lectures, Feynman says:

"... it doesn't matter how clever you are and it doesn't matter what your name is ..."

To analyse the words of Einstein or Feynman in search of the ultimate nature of reality is to succumb to the human longing for an infallible prophet or messiah who produces irrevocable gospel.

What Feynman may or may not have meant by "no one understands QM" - whether it was just a joke, or whether he meant something deeper - is hardly relevant. QM does not stand or fall because of what Eisntein or Feynman once said about it.

 

[gentzen]

You mean that if Feynman knew the Bell's theorem, he wouldn't say this quote?

Since Feynman later learned the lessons of those papers, it should be possible to try to answer your question empirically: When was the last time that he publicly or privately repeated a similar statement? Did he encourage activities to deepen the understanding brought about by the perspective on quantum mechanics of those papers?

A good place to look for an answer to the first question is his book QED from 1985:

The theory of gravitation, on the other hand, was not understandable from the laws of motion, and even today it stands isolated from the other theories. Gravitation is, so far, not understandable in terms of other phenomena.
...
...
... Why are you going to sit here all this time, when you won’t be able to understand what I am going to say? It is my task to convince you not to turn away because you don’t understand it. You see, my physics students don’t understand it either. That is because I don’t understand it. Nobody does.
I’d like to talk a little bit about understanding. When we have a lecture, there are many reasons why you might not understand the speaker. One is, his language is bad - he doesn’t say what he means to say, or he says it upside down - and it’s hard to understand. ...
...
The next reason that you might think you do not understand what I am telling you is, while I am describing to you how Nature works, you won’t understand why Nature works that way. But you see, nobody understands that. I can’t explain why Nature behaves in this peculiar way.

It may sound similar to his statement from 1964. But it is significantly different, because also his previous statement made the comparison with gravitation. In 1964, he suggested that some people understand gravity, but nobody understands quantum mechanics. In 1985, he puts both gravitation and quantum electrodynamics on a similar level, and reduces "not understand" to "you won’t understand why Nature works that way."

For the second question, notice that:

In May 1981, Feynman spoke at a conference on the topic “Simulating physics with computers.” There he proposed the idea of using quantum computers to simulate quantum systems that are too hard to simulate using conventional classical digital computers. Feynman’s talk, later published as a lightly edited transcript [1], is justly remembered for its role in launching quantum computing as a field of study.
[1] Richard P Feynman. Simulating physics with computers, 1981. International Journal of Theoretical Physics, 21(6/7).

Understanding of this perspective on quantum mechanics also deepened because:

In 1981, Herbert proposed FLASH, a scheme for sending signals faster than the speed of light using quantum entanglement. Of this proposal, quantum computing pioneer Asher Peres wrote, "I was the referee who approved the publication of Nick Herbert’s FLASH paper, knowing perfectly well that it was wrong. I explain why my decision was the correct one, and I briefly review the progress to which it led." Chief among the results that Peres claimed stemmed from a refutation of Herbert's proposal was the no-cloning theorem, proved by Wootters, Zurek, and Dieks.

A proof of the no-cloning theorem was already delivered by James Park in 1970, but had no impact at that time.

But Bell only improved the EPR paradox, the "spooky action at distance" was understood by Einstein before Feynman.

Bell's inequality is not a paradox. It was motivated by Bohmian mechanics and the EPR paradox, but that doesn't mean that it proves Bohmian mechanics true, or even resolves the EPR paradox. Bob Doyle in "My God, He Plays Dice! How Albert Einstein Invented Most Of Quantum Mechanics" (2019) wrote:

There may be no “hidden variables,” local or nonlocal. But there are “hidden constants.” Hidden in plain sight, they are the “constants of the motion,” conserved quantities like energy, momentum, angular momentum, and spin, both electron and photon. Created indeterministically when the particles are initially entangled, they then move locally with the now apparently separating particles.

This conservation still is paradoxical for me. In my experience, you should better enforce it exactly in individual scattering events. But it rubs a bit with general relativity. Wolfgang Pauli severely criticised Niels Bohr for being willing to give-up exact conservation, and proposed the neutrino instead (1930). Pauli received the Nobel Price in 1954, the neutrino was discovered experimentally in 1956, and Pauli died in 1958.

 

[vanhees71]

I think what Bell did was much more profound: He translated EPR's pretty vague hypothesis about the existence of a "local realistic theory" into a empirically decidable quantitative alternative by deriving an inequality about certain spin-correlation functions of entangled two-spin systems from the assumption of any local realistic theory that contradicts the prediction of quantum theory about the same correlation function.

The empirical decision is very clear: Quantum theory gives the correct description of the correlation function, and local realistic theories are thus empirically refuted.

 

[gentzen]

Wolfgang Pauli severely criticised Niels Bohr for being willing to give-up exact conservation, and proposed the neutrino instead (1930). Pauli received the Nobel Price in 1954, the neutrino was discovered experimentally in 1956, and Pauli died in 1958.

Sorry, Pauli received the Nobel Prize in 1945, it was Max Born who received it in 1954.

(Also in 1930, Pauli proved that Dirac's holes must have the same mass as the electron, and hence cannot be protons. And in 1934, Pauli and Weisskopf proved that Bosons also have anti-particles. That was intended as a blow against Dirac's hole theory, because it can only make sense for Fermions. Pauli was surprisingly prolific in involuntarily predicting the existence of new particles.)