A proof that magnetic forces do no work?

[Adesh]

The proof of magnetic forces do no work is given in Introduction to Electrodynamics by David J. Griffiths like this

Consider a charged particle $q$ moving with velocity $\mathbf{v}$ in a magnetic field $\mathbf{B}$ then the force on it is $\mathbf{F}= q(\mathbf{v}\times {B})$ and if $q$ moves an amount $d\mathbf{l}=\mathbf{v}dt$, the work done is $$ dW= \mathbf{F} \cdot d\mathbf{l} = q(\mathbf{v}\times \mathbf{B}) \cdot \mathbf{v}dt =0$$ hence, magnetic forces do no work.

My problem is why he has replaced $d\mathbf{l}$ with $\mathbf{v}dt$? This substitution implies that the charged particle was moving with $\mathbf{v}$ only and no force acted on it because when that magnetic force will act on it will cause displacement in a direction perpendicular to $\mathbf{v}$ and force is also in the same direction there the expression for work should not become zero. When he made that substitution he didn't take into account that the direction of velocity will get changed as soon as force comes into the action.

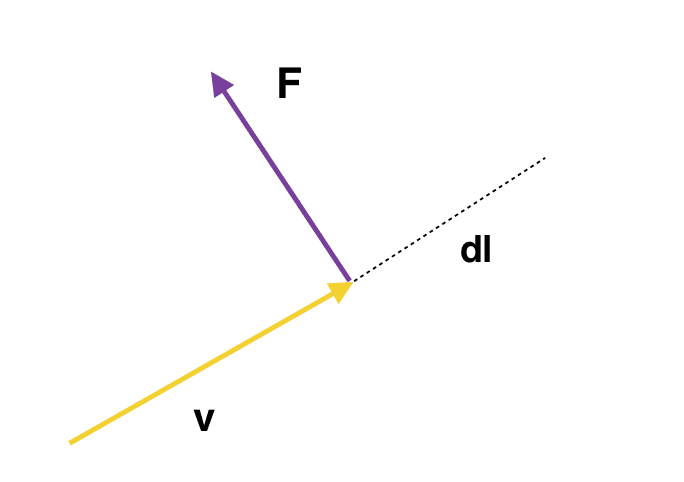I think that particle should move in the direction of the force and we should take $dl$ in the direction of the force and not in the direction of the previous velocity. My main problem is that substitution, $d\mathbf{l} = \mathbf{v}dt$, beaucse what I think is that as force is applied the direction of velocity will get changed and the new velocity $\mathbf{v'}$ will have some direction in the direction of $\mathbf{F}$ and $d\mathbf{l}= \mathbf{v'}dt$. If we assume that $v' = v$ isn't the same thing that we want to prove? However, v' and v and can't have the same direction, the magnetic force would at least change the direction of the velocity.
The definition of work says Force times the displacement in the direction of force and my thinking urges me to believe that the magnetic force would cause a displacement in it’s direction (because particle changes it’s path when magnetic field does work on it).

Thank you.

 

[Vanadium 50]

I think that particle should move in the direction of the force

No. The particle accelerates in the direction of the force. It moves in the direction of the velocity.

 

[Adesh]

No. The particle accelerates in the direction of the force. It moves in the direction of the velocity.

What does it mean to accelerate? Won't it's velocity going to have some component in the direction of acceleration ?

 

[Dale]

What does it mean to accelerate? Won't it's velocity going to have some component in the direction of acceleration ?

Not necessarily. Consider a ball thrown in a typical game of catch. At the beginning of the throw it is moving diagonally forward and up. At the end of the throw it is moving diagonally forward and down. The force is always directly downward, so the ball never moves in the direction of the force. Furthermore, during the first half of the throw there is no component of the velocity in the direction of the force, the component of the velocity is opposite the direction of the force.

The derivation in the OP is correct.

 

[Adesh]

Not necessarily. Consider a ball thrown in a typical game of catch. At the beginning of the throw it is moving diagonally forward and up. At the end of the throw it is moving diagonally forward and down. The force is always directly downward, so the ball never moves in the direction of the force.

The derivation in the OP is correct.

But it does have a component of it's velocity in the direction of force eventually (hence the displacement in the direction of force). Am I right?

 

[Dale]

eventually

Eventually perhaps. For a central force that is never true, but for the ball it is eventually true. However the proof above applies at every instant, not merely eventually.

 

[Adesh]

For a central force that is never true

Can you please explain this?

 

[Dale]

Can you please explain this?

The force is always radial and the velocity is always tangential for a circular orbit. Think of an orbiting satellite.

 

[Adesh]

The force is always radial and the velocity is always tangential for a circular orbit. Think of an orbiting satellite.

Let's consider this picture

When $\mathbf{ F_{B}}$ we see that particle moves inward (that's why it's moving in circle, it responds to the centripetal force). So, what I'm saying why don't we take the displacement that $\mathbf{F_{B}}$ has caused, that little infinitesimal displacement inwards?

 

[Dale]

When $\mathbf{ F_{B}}$ we see that particle moves inward (that's why it's moving in circle, it responds to the centripetal force).

It does not move inwards at any time. At all times the displacement is tangential, not inwards.

In fact, look at the picture you posted. What component of $F_B$ is in the direction of $v$? None. There is no component of the velocity in the direction of the acceleration at any time.

 

[Dale]

This substitution implies that the charged particle was moving with v only and no force acted on it because when that magnetic force will act on it will cause displacement in a direction perpendicular to v and force is also in the same direction there the expression for work should not become zero. When he made that substitution he didn't take into account that the direction of velocity will get changed as soon as force comes into the action.

There is no assumption of any counterfactual $v$ involved. The integral is over the actual velocity resulting from all of the forces and constraints involved. Everything has been accounted for and $v$ is the final resulting velocity for all effects combined.

For calculating the actual work only the actual force and the actual displacement matter. No hypothetical velocities that would have occurred without some force are relevant.

 

[Adesh]

It does not move inwards at any time. At all times the displacement is tangential, not inwards.

In fact, look at the picture you posted. What component of $F_B$ is in the direction of $v$? None. There is no component of the velocity in the direction of the acceleration at any time.

In this picture, I have drawn the violet arrow which represents the velocity after a time $\Delta t$ from where the $+$ sign has been made. I have drawn the components of violet velocity, the components are in yellow color and there you see we have a component inwards. What has caused this inward component of velocity? I think it is $\mathbf{F_{B}}$ which acted at $+$ sign has caused this, correct me if I'm wrong.

 

[Vanadium 50]

You've drawn a force component that doesn't point to the center. Is that what you want?

 

[Dale]

In this picture, I have drawn the violet arrow which represents the velocity after a time Δt from where the + sign has been made.

And at that time what direction is the force? It is perpendicular to the velocity.

I have drawn the components of violet velocity, the components are in yellow color and there you see we have a component inwards.

You have incorrectly drawn the components of the violet velocity. You have drawn the velocity of the particle at $t+\Delta t$ at the location of the particle at $t$ and together with the force on the particle at $t$. It makes no sense whatsoever to draw this. You are placing a future velocity vector on a past location and force. That is nonsense.

There is simply no inward component of velocity at any time. Please see my post 11, which I think you missed.

 

[Nugatory]

I have drawn the violet arrow which represents the velocity after a time $\Delta t$ from where the ++ + sign has been made.

You have... But you should also show the position of the particle after the time $\Delta t$ and the direction of the force when the particle is at that new position. The force will still be perpendicular to the velocity.

How familiar are you with differential calculus? To see this problem clearly, it helps to be comfortable with the limiting procedure used to define the derivative of a function.

 

[Adesh]

You are placing a future velocity vector on a past location and force. That is nonsense.

I didn't get this. How that location is of past?

 

[Adesh]

You've drawn a force component that doesn't point to the center. Is that what you want?

I have drawn the velocity component. Yes I can see that yellow component doesn't point to the center but it is parallel to the $\mathbf{F_{B}}$.

 

[Adesh]

How familiar are you with differential calculus? To see this problem clearly, it helps to be comfortable with the limiting procedure used to define the derivative of a function.

I have attended the Calculus I last year.

You have... But you should also show the position of the particle after the time ΔtΔt\Delta t and the direction of the force when the particle is at that new position. The force will still be perpendicular to the velocity.

My point is that new velocity (that violet arrow at time $t+ \Delta t$ ) was caused by the force that acted on the particle when it was at $+$ sign position.

 

[Nugatory]

I have attended the Calculus I last year.

Good... then you know to drop all terms in $\Delta\theta^2$ (where $\Delta\theta$ is the change in the particle’s tangential position) and higher when you calculate the distance over which the force acts as the particle moves from one position to another, and then take the limit as $\Delta t$ and $\Delta\theta$ both approach zero. It’s worth going through the math for yourself... if you don’t come up with the work done being zero, post your work and we may be able to spot the error.

 

[Dale]

I didn't get this. How that location is of past?

The time $t$ is in the past of the time $t+\Delta t$. You are drawing the velocity at time $t+\Delta t$ at the location at time $t$. A future velocity at a past location. It is complete nonsense.

Again, please see my post 11 which you again appear to have missed.

 

[Vanadium 50]

There are lines and vectors drawn all higgledy-piggledy. We need to step back.

I have a particle moving up with velocity v, and being accelerated to the right with acceleration a. At that moment, what is the velocity magnitude and direction?

 

[Adesh]

There are lines and vectors drawn all higgledy-piggledy. We need to step back.

I have a particle moving up with velocity v, and being accelerated to the right with acceleration a. At that moment, what is the velocity magnitude and direction?

At that moment the velocity is upwards and with a magnitude of $v$.

 

[Vanadium 50]

Good.
Now, why do you draw them differently?

 

[Adesh]

Now, why do you draw them differently?

My violet velocity was caused due to $\mathbf{F_{B}}$, if there were no force then the particle would have continue to travel in same direction, am I right?

 

[Dale]

My violet velocity was caused due to $\mathbf{F_{B}}$, if there were no force then the particle would have continue to travel in same direction, am I right?

Certainly. The question is not about whether the force affects the velocity at all. It is about whether or not the force has a component in the direction of the velocity. It does not. It is perpendicular at all times.

Also, please see post 11

 

[Adesh]

Certainly. The question is not about whether the force affects the velocity at all. It is about whether or not the force has a component in the direction of the velocity. It does not. It is perpendicular at all times.

Also, please see post 11

For calculating the actual work only the actual force and the actual displacement matter

Which displacement? displacement that it has caused (as in the above picture the angular displacement) or the displacement that happened simultaneously to that force (the displacement which was occurring and the force was getting applied ?

 

[Dale]

Which displacement?

There is only one displacement. The actual displacement.

 

[PeroK]

Which displacement? displacement that it has caused (as in the above picture the angular displacement) or the displacement that happened simultaneously to that force (the displacement which was occurring and the force was getting applied ?

If the force by definition is perpendicular to the velocity, then it is always perpendicular to the velocity. As the velocity changes direction the force changes direction to remain perpendicular.

The work done is, therefore, always zero.

 

[Adesh]

There is only one displacement. The actual displacement.

What is actual displacement? That $\Delta \theta$ ?

 

[A.T.]

Which displacement? displacement that it has caused...

Causation doesn't enter the definition of work.

 

[Dale]

What is actual displacement? That $\Delta \theta$ ?

It is the actual path that the object travels. It is a vector, so no, it is not $\Delta \theta$. It is the vector $\Delta \vec r$ which can be written as $\Delta \vec r = \Delta x \hat x + \Delta y \hat y = (\Delta x, \Delta y)$ in Cartesian coordinates or as $\Delta \vec r = \Delta r \hat r + \Delta \theta \hat \theta = (\Delta r, \Delta \theta)$ in polar coordinates. So in polar coordinates you can write it $(0,\Delta \theta)$ and as $\Delta t \to 0$ we get $(0,\Delta \theta/\Delta t) \to (0,d\theta/dt)=(0,v_{\theta})$ which is always perpendicular to the force $(F_B,0)$ and therefore the work is always 0.

 

[Adesh]

Causation doesn't enter the definition of work.

Please explain me a little further, I really want to learn it.

 

[Adesh]

It is the actual path that the object travels. It is a vector, so no, it is not $\Delta \theta$. It is the vector $\Delta \vec r$ which can be written as $\Delta \vec r = \Delta x \hat x + \Delta y \hat y = (\Delta x, \Delta y)$ in Cartesian coordinates or as $\Delta \vec r = \Delta r \hat r + \Delta \theta \hat \theta = (\Delta r, \Delta \theta)$ in polar coordinates. So in polar coordinates you can write it $(0,\Delta \theta)$ and as $\Delta t \to 0$ we get $(0,\Delta \theta/\Delta t) \to (0,d\theta/dt)=(0,v_{\theta})$ which is always perpendicular to the force $(F_B,0)$ and therefore the work is always 0.

But we want to prove that the displacement is perpendicular to the force not the velocity.

 

[Dale]

But we want to prove that the displacement is perpendicular to the force not the velocity.

The velocity is the instantaneous displacement. You have studied calculus.

 

[dsanz]

Please explain me a little further, I really want to learn it.

Forget about what causes what. To calculate work done by a particular force on a given object, you only need to know what that force is and what the displacement of the object is. It doesn't matter whether "only part of the displacement was caused by the force" or anything of that sort. You look at the force and take the dot product with displacement (both at the same instant).