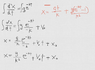- #1
blintaro
- 37
- 1
This is question 1.4 of Chapter 8 of Mary L. Boas's Mathematical Methods in the Physical Sciences, Edition 2. I'm using it as a substitute for my ordinary differential equations class since my textbook has apparently been lost somewhere in the mail.
Find the distance which an object moves in time t if it starts from rest and has an acceleration d^2/dt^2 = ge^(-kt). Show that for a small t the result is approximately (x = 1/2(gt^2)) and for very large t, the velocity dx/dt is approximately constant. (This problem corresponds roughly to the motion of a parachutist.)
The solution manual gives the solution as: x=k^(-1)gt + k^(-2)g(e^(-kt)-1)
I integrated both sides of d^2/dt^2 = ge^(-kt) twice with respect to t, ending up with x = k^(-2)ge^(-kt) + v_0(t) + x_0.
However substituting t=0 into the equation gives x = g/(k^2) + x_0, not (1/2)gt^2, so, obviously on the wrong track.
I put the process in an attached image below since it might be easier to read that than my terrible equation formatting. Thanks!
Homework Statement
Find the distance which an object moves in time t if it starts from rest and has an acceleration d^2/dt^2 = ge^(-kt). Show that for a small t the result is approximately (x = 1/2(gt^2)) and for very large t, the velocity dx/dt is approximately constant. (This problem corresponds roughly to the motion of a parachutist.)
Homework Equations
The solution manual gives the solution as: x=k^(-1)gt + k^(-2)g(e^(-kt)-1)
The Attempt at a Solution
I integrated both sides of d^2/dt^2 = ge^(-kt) twice with respect to t, ending up with x = k^(-2)ge^(-kt) + v_0(t) + x_0.
However substituting t=0 into the equation gives x = g/(k^2) + x_0, not (1/2)gt^2, so, obviously on the wrong track.
I put the process in an attached image below since it might be easier to read that than my terrible equation formatting. Thanks!