Novus
- 19
- 1
- TL;DR Summary
- Recently I've become interested in the bottom and side case exceptions to Archimedes' Principle for which a limited number of interesting scientific papers can be found on-line.
First post on this forum, hopefully in the correct category and conforming to forum rules.
Will the object in below scenario move upwards, downwards or will it remain stationary?
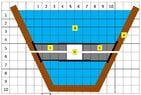
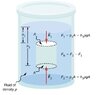
An object is submersed in a container 'A' which contains a fluid 'B' (e.g. water)
The trapezium shaped object consists of two seperate parts which enclose each other in such a way that no water can seep in and, as a a result, can expand in a horizontal plane.
The submersed object consists of solid area's 'C' with the same density as water and a volume of air 'D' which can expand or compress in a horizontal plane. The volume of air 'D' is connected to the air outside of the container via air tubes.
It is given that, without going in further detail that "The sides of the object are 'embedded' water tight on a 'sliding system' inside the container wall" The object can move up or down whereby, as a result, the volume of air will either increase or decrease.
Each square in the picture is 1 cm2. The object has a width of 1 cm. The width of the container is > 1 cm.
The top of the object is at a dept of 4 cm and the bottom at a dept of 6 cm. The area of the top of the object is 10 cm2 and the area of the bottom of the object is 8 cm2.
The hydrostatic pressure on the bottom of the object will, as a result, exceed the hydrostatic pressure at the top of the object?
Will the object in below scenario move upwards, downwards or will it remain stationary?
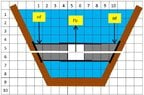
An object is submersed in a container 'A' which contains a fluid 'B' (e.g. water)
The trapezium shaped object consists of two seperate parts which enclose each other in such a way that no water can seep in and, as a a result, can expand in a horizontal plane.
The submersed object consists of solid area's 'C' with the same density as water and a volume of air 'D' which can expand or compress in a horizontal plane. The volume of air 'D' is connected to the air outside of the container via air tubes.
It is given that, without going in further detail that "The sides of the object are 'embedded' water tight on a 'sliding system' inside the container wall" The object can move up or down whereby, as a result, the volume of air will either increase or decrease.
Each square in the picture is 1 cm2. The object has a width of 1 cm. The width of the container is > 1 cm.
The top of the object is at a dept of 4 cm and the bottom at a dept of 6 cm. The area of the top of the object is 10 cm2 and the area of the bottom of the object is 8 cm2.
The hydrostatic pressure on the bottom of the object will, as a result, exceed the hydrostatic pressure at the top of the object?