A wheel of radius r rolls along a curve

[annamal]

Homework Statement

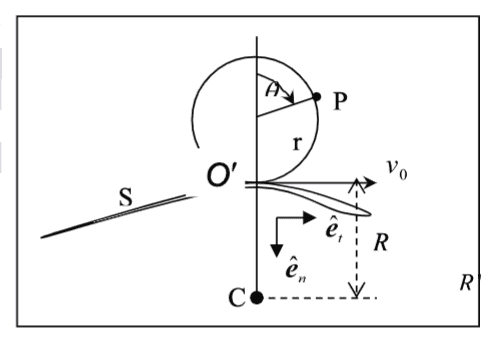
A wheel of radius r rolls along a general convex curve of varying radius of curvature R such that all motion is confined to a single plane. The contact point O’ traverses the curve at a constant speed v0 . Find the absolute velocity and acceleration of a point P on the rim.

Relevant Equations

v = dr/dt
a = dv/dt

How does this wheel roll? The velocity at the base where the curve is is facing to the right, but the theta direction seems to imply the wheel is rolling clockwise which would mean the velocity with the curve should be facing to the left. Does anyone have clarity what is going on in the picture below?

 

[haruspex]

The point of the wheel instantaneously in contact with the curve is necessarily instantaneously at rest. But which point of the wheel makes contact changes over time, as does the point on the curve contacted. The velocity vector shown refers to the instantaneous motion of where contact is being made on the curve.

 

[annamal]

The point of the wheel instantaneously in contact with the curve is necessarily instantaneously at rest. But which point of the wheel makes contact changes over time, as does the point on the curve contacted. The velocity vector shown refers to the instantaneous motion of where contact is being made on the curve.

So are you saying the wheel is not slipping? The problem statement seems to imply slipping because of the velocity vector in contact with the curve at the base

 

[haruspex]

The problem statement seems to imply slipping because of the velocity vector in contact with the curve at the base

No, you are misreading the question. When it says the contact point moves at speed v0 it does not mean that a particular bit of the wheel moves at that speed.
Imagine taking a film of a rolling wheel. In each frame, mark where it contacts the road. When you run the film, how fast does your mark move?

 

[annamal]

No, you are misreading the question. When it says the contact point moves at speed v0 it does not mean that a particular bit of the wheel moves at that speed.
Imagine taking a film of a rolling wheel. In each frame, mark where it contacts the road. When you run the film, how fast does your mark move?

I took a look at the solutions and it does seem like v_O'/C is moving at velocity v0 because v_O'/C = v0*vec e_t. Equations 3 and 4 below:

 

[haruspex]

it does seem like v_O'/C is moving at velocity v0

Sure, but O' is not the same physical piece of the wheel over time. At any given time t, it is where in space the wheel contacts the curve at that instant. I.e., the mark I described in post #4. $v_0$ is how fast the mark moves.

 

[annamal]

Sure, but O' is not the same physical piece of the wheel over time. At any given time t, it is where in space the wheel contacts the curve at that instant. I.e., the mark I described in post #4. $v_0$ is how fast the mark moves.

Ok, I see that. But why isn't the velocity of the base v0 = 0 then b/c it doesn't move?

 

[haruspex]

Ok, I see that. But why isn't the velocity of the base v0 = 0 then b/c it doesn't move?

The velocity of the bit of the wheel instantaneously in contact is zero. You can think of it as the wheel rotating about that point, if it helps.
A wheel radius r moving at speed v flat road rotates at rate $\omega=v/r$. In time dt it moves along vdt and rotates through angle $\omega dt$. The bit of wheel at the top has moved approximately $r\sin(\omega dt)\approx r\omega dt=vdt$ further than the middle, so is moving at speed 2v. Likewise, the bit in contact with ground has moved approximately $r\sin(\omega dt)\approx r\omega dt=vdt$ less far than the middle, so is moving at speed 0.

 

[annamal]

The velocity of the bit of the wheel instantaneously in contact is zero. You can think of it as the wheel rotating about that point, if it helps.
A wheel radius r moving at speed v flat road rotates at rate $\omega=v/r$. In time dt it moves along vdt and rotates through angle $\omega dt$. The bit of wheel at the top has moved approximately $r\sin(\omega dt)\approx r\omega dt=vdt$ further than the middle, so is moving at speed 2v. Likewise, the bit in contact with ground has moved approximately $r\sin(\omega dt)\approx r\omega dt=vdt$ less far than the middle, so is moving at speed 0.

I think the problem is not saying that the contact point has an instantaneous velocity of 0 when it says the contact point traverses with v0. I am confused about why the problem has to say the contact point traverses with v0 and not just say the wheel traverses the hill without slipping if the contact point has instantaneous velocity of 0.

 

[haruspex]

I think the problem is not saying that the contact point has an instantaneous velocity of 0 when it says the contact point traverses with v0. I am confused about why the problem has to say the contact point traverses with v0 and not just say the wheel traverses the hill without slipping if the contact point has instantaneous velocity of 0.

Consider a disc radius r rolling around the outside of a circle radius R.
The contact point on the circle rotates around at rate $\omega$ and linear speed $R\omega$. The centre of the disc moves around the circle at the same angular rate, so at linear speed $(R+r)\omega$.
If, instead of rolling, the disc were sliding around so that its contact point were always the same bit of it then in time t the disc has rotated an angle rate $\omega t$. But since it is rolling, the length of arc on the perimeter of the circle that has been the contact point is the same as the length of arc on the perimeter of the disc that has been the contact point. That means the disc has rotated on its own centre an additional $\frac Rr\omega t$. Hence, the disc rotates about its own centre at rate $(1+\frac Rr)\omega$.
E.g. with r=R, after going half way round the circle the disc has performed a complete revolution on its own centre and is the same way "up" as it started.

In the question, $v_0$ is the speed at which the contact point on the ground moves. If at such a point the radius of curvature of the ground is R (and the centre of curvature is below ground) then the speed of the disc's centre is $\frac{R+r}rv_0$.

 

[annamal]

In the question, $v_0$ is the speed at which the contact point on the ground moves. If at such a point the radius of curvature of the ground is R (and the centre of curvature is below ground) then the speed of the disc's centre is $\frac{R+r}rv_0$.

Ok, so the contact point on the ground is moving? Like the contact point is sliding with respect to the ground?

 

[erobz]

Ok, so the contact point on the ground is moving? Like the contact point is sliding with respect to the ground?

The point of contact translates. The point of contact is where the wheel touches the ground at an instant. An instant later the point of contact ( a different point on the wheel) is not where it was a moment ago. It’s moving along with the wheel( in space). Imagine you paint the tire, and roll it on flat ground. The velocity of the point of contact is the change in length of that paint line per unit time.

 

[haruspex]

Ok, so the contact point on the ground is moving? Like the contact point is sliding with respect to the ground?

Yes.

 

[jbriggs444]

The contact point is something like the intersection point of a pair of scissors. Its motion is that of an imaginary point, not the motion of any material thing. Calling it "sliding" does not seem apt.