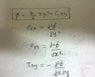Airys stress function -- structures

Click For Summary
SUMMARY

The discussion focuses on deriving the stress function for a simply supported beam subjected to a concentrated load at mid-span, represented by the equation (fi) = (b/6) x y³ + C*xy. The user seeks to establish boundary conditions, specifically that (sigma)yy = 0 for y = h to -h, and (tou)xy = 0 at y = -h and y = h. The goal is to ensure the stress function satisfies the loading conditions, particularly the shear stress distribution related to the concentrated load.

PREREQUISITES
  • Understanding of beam theory and stress analysis
  • Familiarity with boundary conditions in structural mechanics
  • Knowledge of shear stress distribution in beams
  • Proficiency in mathematical integration techniques
NEXT STEPS
  • Research the derivation of stress functions in elasticity theory
  • Learn about boundary value problems in structural mechanics
  • Study shear stress distribution methods for beams under concentrated loads
  • Explore the application of the Airy stress function in two-dimensional problems
USEFUL FOR

Students and professionals in structural engineering, particularly those focusing on beam analysis and stress distribution methods in mechanics.

praveenpandiyan
Messages
28
Reaction score
1

Homework Statement


For (fi)= (b/6) x*y3 +C*xy show that simply supported beam of 2L loaded concentrated load at mid span.,the stress function satisfy loading condition is (fi) .treat concentrated load as shear stress suitably distributed to shoot this function. so that intergtal of limit (h to -h) for stress stress (tou)xy= (-W/2) ..

Homework Equations


see attachment

The Attempt at a Solution


boundary conditions 1. (sigma)yy=0 for y =h to -h
to remove constants in stress function i need one more boundary condition .. ?? any help ll be apreciated . thanks
 

Attachments

  • WP_20150113_001.jpg
    WP_20150113_001.jpg
    35.4 KB · Views: 469
Physics news on Phys.org
i found other boundary condition too ..beam shear stess (tou)xy=o at y=(-h &=+h)..thanks anyway ..
 

Similar threads

Cantilever Beam subjected to shear stress
  • · Replies 1 ·
Replies
1
Views
5K
Verification of stress function
  • · Replies 1 ·
Replies
1
Views
2K
Solve Plane Elasticity w/ Airy Stress Function
  • · Replies 3 ·
Replies
3
Views
2K
Graduate Prospects of spin foam formalism in loop quantum gravity [Alexandrov, Roche]
  • · Replies 9 ·
Replies
9
Views
7K