zenterix
- 774
- 84
- TL;DR Summary
- I'm writing this post to perhaps come one step closer to finally understanding why we use the associated variables convention when analyzing electric circuits.
Consider the following circuit
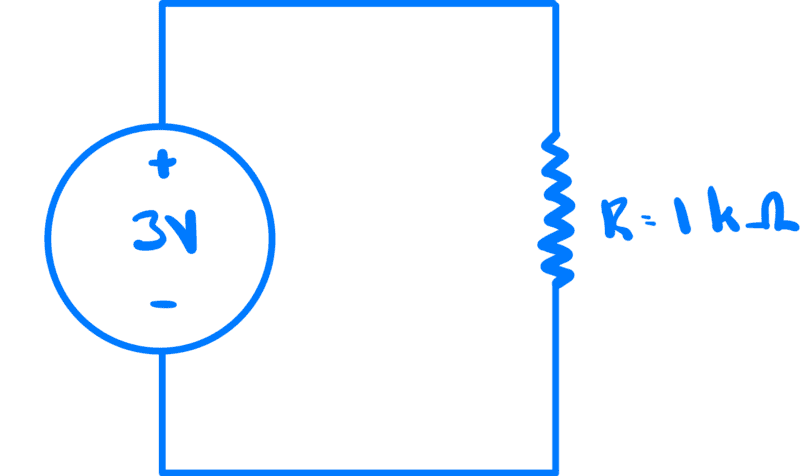
The first thing we do is to label each terminal of each circuit element. We use the labels + and -.
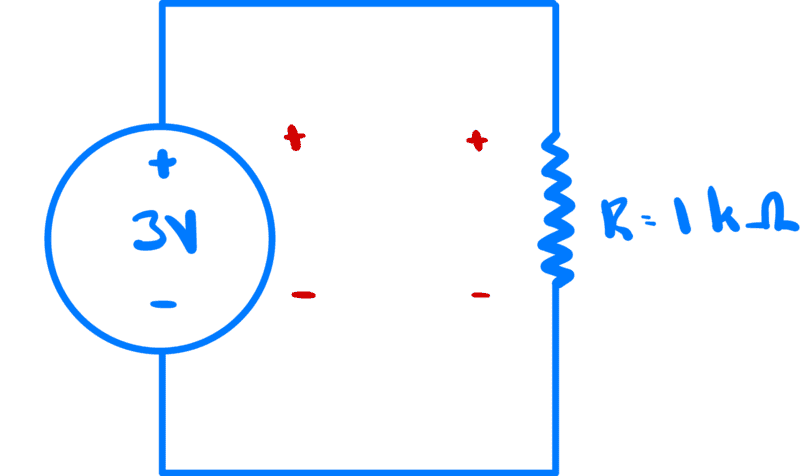
We could assign these differently (and I will do this in a second example further below), but for now let's stick with these labels.
Next, we assign terminal variables. For each circuit element, we have a current going into the positive label. We also have a variable for each circuit element denoting the difference in potential between the + terminal and the - terminal.
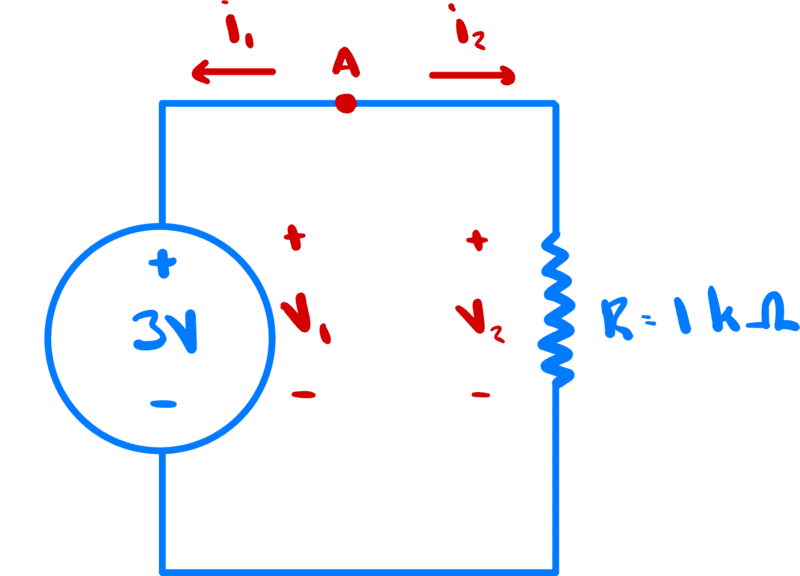
Since our choice of voltage terminal labelling coincides with the battery's actual positive and negative terminals, we immediately know that ##v_1=3\text{V}## and with KVL we can show that ##v_1=v_2=3\text{V}##.
With KCL we can see that ##-i_1-i_2=0## so ##i_1=-i_2##
Given ##R## we know that ##i_2=\frac{v_2}{R}=3\cdot10^{-3}\text{A}##.
Thus, ##i_1=-3\cdot10^{-3}\text{A}##.
What can we say about power?
Without using the conventions at all, let's just consider the battery. The battery itself has a terminal with a higher potential and a terminal with a lower potential due simply to the way the battery works (this is independent of how we choose to label the terminals).
When the battery is not being charged, positive current flows through the battery from lower to higher potential, and once it leaves the battery flows from higher to lower potential. When this current flows through the battery, each coulomb of charge gains 3J of electric potential energy.
Since the current flowing through the battery is ##-i_1=3\cdot10^{-3}\text{A}## coulombs per second, then the battery is generating ##9\cdot10^{-3}\mathrm{\frac{J}{s}}##, ie
$$9\cdot10^{-3}\text{W}$$
Now consider the resistor. When positive current passes through the resistor it goes from a higher to a lower potential, thus losing electric potential energy. The amount of energy "generated" when current passes through the resistor is $$i_2\cdot (v_2^--v_2^+))=3\cdot10^{-3}\text{A}\cdot (-3\text{V})=-9\cdot10^{-3}\text{W}$$
This is negative energy generation, and thus we say that the resistor dissipates energy.
This is not, however, how we think about power when we use the associated variables convention.
The convention is to calculate power by multiplying the current variable into the positively labeled terminal by the voltage terminal.
Thus, we have that "power into the battery" is
$$i_1v_1=-3\cdot10^{-3}\text{A}\cdot 3\text{V}=-9\cdot10^{-3} \text{W}$$
and "power into the resistor" is
$$i_2v_2=3\cdot10^{-3}\text{A}\cdot 3\text{V}=9\cdot10^{-3} \text{W}$$
Compared to the way we calculated power previously, the signs are reversed.
The reason for this, semantically as I understand it, is that in the first case we calculated "power through the circuit element" and in the second case we calculated "power into the circuit element given our choice terminal variables".
Power through the circuit element means we're not even considering terminal variables. We are considering the actual circuit element (including the difference of potential on its terminals) and the actual flow of positive current between terminals. Depending on the circuit that the element is in, the current might flow from terminal A to terminal B or from terminal B to terminal A.
Power into the circuit element given our choice of terminal variables means that no matter what the circuit element is, we always perform the same calculation given the terminal variables: voltage at the positive terminal minus voltage at the negative terminal, times the current into the positive terminal.
Turns out that in both possible ways of assigning the voltages to a two-terminal circuit element, the result of this calculation is the same.
For example, consider the following change in the terminal voltage variables of the battery
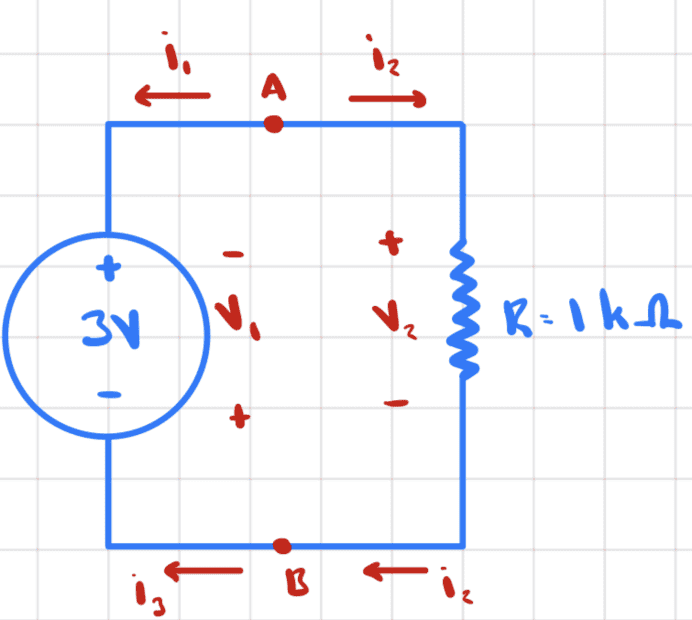
##i_3## turns out to be the negative of ##i_1## and is the current going into the positive terminal voltage on the battery. Recall that previously, the incoming current was ##i_1##.
However, the diference in potential (which is the potential at the positive terminal minus at the negative terminal) is actually the potential at the battery's negative potential minus the battery's positive potential. Previously, it was the opposite (battery's positive potential minus battery's negative potential), so this also changed signs).
Therefore, when we calculate the power into the battery, the result is the same as before
$$i_3v_1=(-i_1)\cdot(v_1^+-v_1^-)=-i_1\cdot (-3)=3i_1<0$$
My conclusion is that the associated variables convention exists to try to minimize the errors involved in manually doing these calculations.
If we remember to
1) Label the terminals
2) Assign current and voltage terminal variables
3) Calculate power as incoming into positive terminal times incoming potential minus outgoing potential
then we get results that we can always interpret in the same way: negative power means power is being supplied and positive power means power is being dissipated.
One thing I didn't touch on is Ohm's law, which I think is actually the most crucial aspect of all of this discussion.
It is Ohm's law that relates voltage difference to current, in a very specific way.
According to Ohm's law, voltage where current is incoming minus voltage where current is outgoing is equal to incoming current times resistance.
This is the empirical law that we know.
The convention tells us to always measure potential difference this way (ie, incoming minus outgoing) and to measure the current as the incoming current. Thus, the way we set our variables in the convention allows us to directly apply Ohm's law without having to think about signs.
On the other hand, when we think about power, we do have to think about signs. We have to remember that the convention is that negative means power supplied and positive means power dissipated, even though from the point of view strictly of the equations, units, and concepts, I am not sure that these signs make sense.
That is (final point), I am not sure how to interpret, in an a way that is not simply based on the convention, that the power into the battery is negative. After all, actual positive current flowing through the battery gains potential energy, and so does negative current flowing in the opposite direction.
The first thing we do is to label each terminal of each circuit element. We use the labels + and -.
We could assign these differently (and I will do this in a second example further below), but for now let's stick with these labels.
Next, we assign terminal variables. For each circuit element, we have a current going into the positive label. We also have a variable for each circuit element denoting the difference in potential between the + terminal and the - terminal.
Since our choice of voltage terminal labelling coincides with the battery's actual positive and negative terminals, we immediately know that ##v_1=3\text{V}## and with KVL we can show that ##v_1=v_2=3\text{V}##.
With KCL we can see that ##-i_1-i_2=0## so ##i_1=-i_2##
Given ##R## we know that ##i_2=\frac{v_2}{R}=3\cdot10^{-3}\text{A}##.
Thus, ##i_1=-3\cdot10^{-3}\text{A}##.
What can we say about power?
Without using the conventions at all, let's just consider the battery. The battery itself has a terminal with a higher potential and a terminal with a lower potential due simply to the way the battery works (this is independent of how we choose to label the terminals).
When the battery is not being charged, positive current flows through the battery from lower to higher potential, and once it leaves the battery flows from higher to lower potential. When this current flows through the battery, each coulomb of charge gains 3J of electric potential energy.
Since the current flowing through the battery is ##-i_1=3\cdot10^{-3}\text{A}## coulombs per second, then the battery is generating ##9\cdot10^{-3}\mathrm{\frac{J}{s}}##, ie
$$9\cdot10^{-3}\text{W}$$
Now consider the resistor. When positive current passes through the resistor it goes from a higher to a lower potential, thus losing electric potential energy. The amount of energy "generated" when current passes through the resistor is $$i_2\cdot (v_2^--v_2^+))=3\cdot10^{-3}\text{A}\cdot (-3\text{V})=-9\cdot10^{-3}\text{W}$$
This is negative energy generation, and thus we say that the resistor dissipates energy.
This is not, however, how we think about power when we use the associated variables convention.
The convention is to calculate power by multiplying the current variable into the positively labeled terminal by the voltage terminal.
Thus, we have that "power into the battery" is
$$i_1v_1=-3\cdot10^{-3}\text{A}\cdot 3\text{V}=-9\cdot10^{-3} \text{W}$$
and "power into the resistor" is
$$i_2v_2=3\cdot10^{-3}\text{A}\cdot 3\text{V}=9\cdot10^{-3} \text{W}$$
Compared to the way we calculated power previously, the signs are reversed.
The reason for this, semantically as I understand it, is that in the first case we calculated "power through the circuit element" and in the second case we calculated "power into the circuit element given our choice terminal variables".
Power through the circuit element means we're not even considering terminal variables. We are considering the actual circuit element (including the difference of potential on its terminals) and the actual flow of positive current between terminals. Depending on the circuit that the element is in, the current might flow from terminal A to terminal B or from terminal B to terminal A.
Power into the circuit element given our choice of terminal variables means that no matter what the circuit element is, we always perform the same calculation given the terminal variables: voltage at the positive terminal minus voltage at the negative terminal, times the current into the positive terminal.
Turns out that in both possible ways of assigning the voltages to a two-terminal circuit element, the result of this calculation is the same.
For example, consider the following change in the terminal voltage variables of the battery
##i_3## turns out to be the negative of ##i_1## and is the current going into the positive terminal voltage on the battery. Recall that previously, the incoming current was ##i_1##.
However, the diference in potential (which is the potential at the positive terminal minus at the negative terminal) is actually the potential at the battery's negative potential minus the battery's positive potential. Previously, it was the opposite (battery's positive potential minus battery's negative potential), so this also changed signs).
Therefore, when we calculate the power into the battery, the result is the same as before
$$i_3v_1=(-i_1)\cdot(v_1^+-v_1^-)=-i_1\cdot (-3)=3i_1<0$$
My conclusion is that the associated variables convention exists to try to minimize the errors involved in manually doing these calculations.
If we remember to
1) Label the terminals
2) Assign current and voltage terminal variables
3) Calculate power as incoming into positive terminal times incoming potential minus outgoing potential
then we get results that we can always interpret in the same way: negative power means power is being supplied and positive power means power is being dissipated.
One thing I didn't touch on is Ohm's law, which I think is actually the most crucial aspect of all of this discussion.
It is Ohm's law that relates voltage difference to current, in a very specific way.
According to Ohm's law, voltage where current is incoming minus voltage where current is outgoing is equal to incoming current times resistance.
This is the empirical law that we know.
The convention tells us to always measure potential difference this way (ie, incoming minus outgoing) and to measure the current as the incoming current. Thus, the way we set our variables in the convention allows us to directly apply Ohm's law without having to think about signs.
On the other hand, when we think about power, we do have to think about signs. We have to remember that the convention is that negative means power supplied and positive means power dissipated, even though from the point of view strictly of the equations, units, and concepts, I am not sure that these signs make sense.
That is (final point), I am not sure how to interpret, in an a way that is not simply based on the convention, that the power into the battery is negative. After all, actual positive current flowing through the battery gains potential energy, and so does negative current flowing in the opposite direction.
Last edited: