- #1
Tomas Vencl
- 66
- 13
- TL;DR Summary
- curved spacetine 2 dimensional diagram
Ispired by PeterDonis remark about "river model" in some thread a time ago I made next visualization picture.
The graph desctibes, how the flat Minkowski spacetime is changed in presence of mass (black hole). It do not need much explanation, almost everything is described at the picture. To me it seems to be very ilustrating, so maybe, it can help someone. Please, any notes and remarks are welcomed.
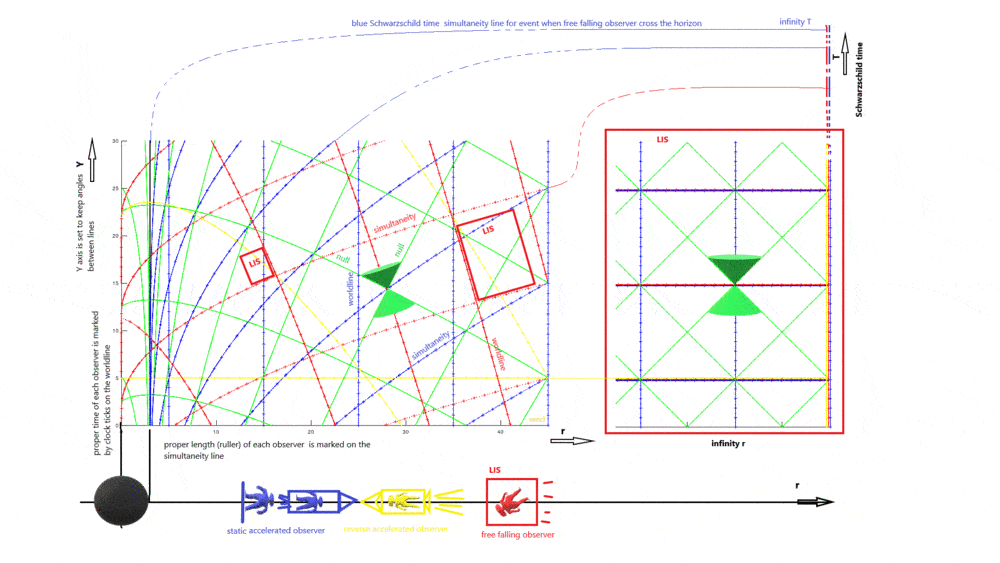
The graph desctibes, how the flat Minkowski spacetime is changed in presence of mass (black hole). It do not need much explanation, almost everything is described at the picture. To me it seems to be very ilustrating, so maybe, it can help someone. Please, any notes and remarks are welcomed.