Apparent position and light travel time
Join the discussion
Registration is free. Ask a follow-up in this thread, or start your own.
77 replies · 17K views
gonegahgah
- 376
- 0
Thanks All. So the answer is provided as "yes, the blink will arrive at the eye from both bulbs at the same time." I will explore this more here later.
Randall, good clarifications. You mention the doppler shift which I agree with.
Taking the following diagram at Wikipedia that 1effect kindly provided:
http://upload.wikimedia.org/wikipedia/en/e/e0/XYCoordinates.gif"
One thing it depicts is that for the observer who is moving is that the further objects are away to the side (that are stationary) the more they appear red shifted as the observer accelerates.
In my diagram the bulb is moving instead of the observer but that is just a relative consideration. We could consider the moving bulb to be stationary and that the eye is moving instead; it is all the same. In either respect I would expect as the Wikipedia diagram shows that the moving bulb would appear to do its one blink red shifted to the eye; while the stationary bulb would blink yellow.
That is correct; is it not?
Randall, good clarifications. You mention the doppler shift which I agree with.
Taking the following diagram at Wikipedia that 1effect kindly provided:
http://upload.wikimedia.org/wikipedia/en/e/e0/XYCoordinates.gif"
One thing it depicts is that for the observer who is moving is that the further objects are away to the side (that are stationary) the more they appear red shifted as the observer accelerates.
In my diagram the bulb is moving instead of the observer but that is just a relative consideration. We could consider the moving bulb to be stationary and that the eye is moving instead; it is all the same. In either respect I would expect as the Wikipedia diagram shows that the moving bulb would appear to do its one blink red shifted to the eye; while the stationary bulb would blink yellow.
That is correct; is it not?
Last edited by a moderator:
gonegahgah
- 376
- 0
Doc, Randall, is that correct?
The following diagram I've drawn shows this doesn't it? It depicts the bulb with the eye moving by it at .6c. As in the first example the bulbs blink at point of contact which is when the eye is directly in line with the bulbs as per the bulb that it stays stationary relative to. The eye continues moving to the left relative to the moving bulb.
However as you said Randall the time the light takes to travel needs to be taken into account. By the time the light reaches the eye, the eye has now reached a position where it is moving away from the bulb. So the blink should be yellow for the bulb that remains stationary with respect to the eye; but should blink redder for the other bulb in the example that is moving in relation to the eye.
Doc and Randall, can you tell me whether that is correct or not?
The following diagram I've drawn shows this doesn't it? It depicts the bulb with the eye moving by it at .6c. As in the first example the bulbs blink at point of contact which is when the eye is directly in line with the bulbs as per the bulb that it stays stationary relative to. The eye continues moving to the left relative to the moving bulb.
However as you said Randall the time the light takes to travel needs to be taken into account. By the time the light reaches the eye, the eye has now reached a position where it is moving away from the bulb. So the blink should be yellow for the bulb that remains stationary with respect to the eye; but should blink redder for the other bulb in the example that is moving in relation to the eye.
Doc and Randall, can you tell me whether that is correct or not?
Attachments
RandallB
- 1,550
- 0
No not quite, (I'd like your diagram better if it compared just before and after reaching the perpendicular point).gonegahgah said:
I prefer the link from Dr Al, from that you should have picked up that the travel time for light was not the issue, nor what I had said. My comment was “might you consider the rate of time being used to source the light".
The point is you no longer have a Doppler Effect as if you were track side listening to a train and its whistle go by; It sounds different than the one parked next to you as it comes towards you or away from you, but for the instant it passes by it sounds the same. Why shouldn’t light behave the same way?
The source of light passing by relative to your observer is experiencing time at a slower rate thus as yellow light is cycling at a slower rate than yellow light generated in the observer frame and thus measured in the observer frame as having a longer (red shifted) wavelength.
Of course any observer moving with the source would experience the same ‘slow time’ and contracted lengths that define how the light is generated and will see the light as yellow.
The reason your observer sees red is because of the time rate difference between the two frames, not the Doppler Effect or any change in the “travel time for light”.
gonegahgah
- 376
- 0
I was going to get to sound in my next post. The main difference between sound and light of course is that sound requires a medium to travel through and light does not. I'll explore this difference tonight and ask for your feedback.
But ultimately the answer you have given is "yes, the observer will see the moving bulb do its one blink as redder than the stationary bulb" in this example. That is what I read in your reply. That is correct isn't it?
But ultimately the answer you have given is "yes, the observer will see the moving bulb do its one blink as redder than the stationary bulb" in this example. That is what I read in your reply. That is correct isn't it?
RandallB
- 1,550
- 0
Yes your result is correct
The issue is the cause of the "Transverse Doppler effect" :
A relative difference in time and how distance is measured between the two frames in the case of the light problem. (Again not the traditional Doppler Effect or any change in the “travel time for light”)
There is no significant difference in how time and distance is measured between frames with speed differences that apply to sound problems – hence there is no such thing as a "Transverse Doppler effect" for a sound example AFAIK.
The issue is the cause of the "Transverse Doppler effect" :
A relative difference in time and how distance is measured between the two frames in the case of the light problem. (Again not the traditional Doppler Effect or any change in the “travel time for light”)
There is no significant difference in how time and distance is measured between frames with speed differences that apply to sound problems – hence there is no such thing as a "Transverse Doppler effect" for a sound example AFAIK.
gonegahgah
- 376
- 0
Thanks Randall.
Onto sound as I mentioned.
I've drawn some diagrams to depict the movement of sound through the air.
Each of the diagrams shows an observer (or listener), an emitter (a horn) and the transmission of the sound. It is an amazing horn because it produces a pure harmonic wave sound.
To the left is depicted what I expect the listener to hear.
Each of the diagrams shows a few things:
- the pitch of the wave relative to the air it moves through
- how long the wave takes to reach the listener (either 3 or 6 units of time)
- the relative movement of each of the actors either stationary or half speed of sound.
The actors include the listener, the horn, the sound and also the air mass through which the sound moves.
The 1st diagram depicts the listener, horn and air mass as all stationary. This is the base diagram for comparison.
The 2nd diagram depicts only the listener moving. As can be seen the sound gets to the listener in half the time and is twice the pitch.
The 3rd diagram depicts only the horn moving. As can be seen the sound takes the normal time to reach the listener but is twice the pitch.
The 4th diagram depicts only the air mass moving. This is the interesting as you can see the sound takes half the time to reach the listener but they hear a normal pitch.
The 5th diagram depicts the person and horn moving together. The listener hears the sound in half the time but at normal pitch.
Hopefully Randall (hopefully you will too Doc) you will agree with all these diagrams.
What they show is that the speed of sound is dependent on the movement of the air mass relative to the receiver (or vice versa if measuring from the receiver).
The diagrams should basically agree with real life experience.
1st) Whether an emitter is moving or not the sound will take the same amount of time to reach us.
2nd) If we move towards an emitter the sound will take less time to reach us.
3rd) As per 1st but if the emitter is moving it will change the pitch we hear.
5th) If you are in a car following another car the car in front will sound normal just as the last diagram shows (though the sound will reach you quicker)...
4th) and this is basically the same as the 5th diagram. If an air mass is traveling toward you then the sound it carries will travel towards you with its added speed.
From the diagrams it can be seen that the pitch you hear for sound is determined by the relative speed of emitter to you (I'll add after time delay and direction effects are taken into account but we can discuss that later), but the time taken for the sound to reach you is affected by the relative speed of the air masses around you.
Can you examine this and tell me what you think Randall & Doc.
Onto sound as I mentioned.
I've drawn some diagrams to depict the movement of sound through the air.
Each of the diagrams shows an observer (or listener), an emitter (a horn) and the transmission of the sound. It is an amazing horn because it produces a pure harmonic wave sound.
To the left is depicted what I expect the listener to hear.
Each of the diagrams shows a few things:
- the pitch of the wave relative to the air it moves through
- how long the wave takes to reach the listener (either 3 or 6 units of time)
- the relative movement of each of the actors either stationary or half speed of sound.
The actors include the listener, the horn, the sound and also the air mass through which the sound moves.
The 1st diagram depicts the listener, horn and air mass as all stationary. This is the base diagram for comparison.
The 2nd diagram depicts only the listener moving. As can be seen the sound gets to the listener in half the time and is twice the pitch.
The 3rd diagram depicts only the horn moving. As can be seen the sound takes the normal time to reach the listener but is twice the pitch.
The 4th diagram depicts only the air mass moving. This is the interesting as you can see the sound takes half the time to reach the listener but they hear a normal pitch.
The 5th diagram depicts the person and horn moving together. The listener hears the sound in half the time but at normal pitch.
Hopefully Randall (hopefully you will too Doc) you will agree with all these diagrams.
What they show is that the speed of sound is dependent on the movement of the air mass relative to the receiver (or vice versa if measuring from the receiver).
The diagrams should basically agree with real life experience.
1st) Whether an emitter is moving or not the sound will take the same amount of time to reach us.
2nd) If we move towards an emitter the sound will take less time to reach us.
3rd) As per 1st but if the emitter is moving it will change the pitch we hear.
5th) If you are in a car following another car the car in front will sound normal just as the last diagram shows (though the sound will reach you quicker)...
4th) and this is basically the same as the 5th diagram. If an air mass is traveling toward you then the sound it carries will travel towards you with its added speed.
From the diagrams it can be seen that the pitch you hear for sound is determined by the relative speed of emitter to you (I'll add after time delay and direction effects are taken into account but we can discuss that later), but the time taken for the sound to reach you is affected by the relative speed of the air masses around you.
Can you examine this and tell me what you think Randall & Doc.
Attachments
Last edited:
gonegahgah
- 376
- 0
I should add the horn only makes one honk. The separate waves represent the honk at each time interval ie after 1 time unit, after 2 time unit, 3 time unit, 4 time unit, 5 time unit, 6 time unit.
The dotted actors represent where the actors were when the horn honked and the solid actors represent where they are when the listener hears the sound.
The sound wave lengths shown can also be considered as their lengths if time were frozen as well as representing their frequency relative to the air mass as mentioned.
The dotted actors represent where the actors were when the horn honked and the solid actors represent where they are when the listener hears the sound.
The sound wave lengths shown can also be considered as their lengths if time were frozen as well as representing their frequency relative to the air mass as mentioned.
RandallB
- 1,550
- 0
You might include a code for the wave form to indicate pitch heard.
N Normal, H High, L Low.
I interpret the shape of the wave forms in each left side ear diagram to be from top down as N, H, H, N, N.
With a speed near “S” or higher for the source you create a standing wave holding more and more energy (a sonic boom). Not sure how you want to show that and of course light does not do that.
(edit added comment)
So your notes are reasonable, but incomplete as they do not define how in some cases the volume is significantly affected as well. Example the horn can be made to move at a speed of 1.1s - faster than sound moves in the air; so upon reaching the observer the newer sounds will be heard very shortly before the older sounds. Not sure how you match up the phases of those – the energy contained in those sounds would not be canceled out by out of phase conditions. Glass breaking sonic booms from real tests show that energy remains very real.
I suppose these could demonstrate characteristics sound has that light does not display; in contrast to the "Transverse Doppler effect" light displays which sound does not.
So Yes your notes look ok, just be alert to faster than sound considerations
N Normal, H High, L Low.
I interpret the shape of the wave forms in each left side ear diagram to be from top down as N, H, H, N, N.
With a speed near “S” or higher for the source you create a standing wave holding more and more energy (a sonic boom). Not sure how you want to show that and of course light does not do that.
(edit added comment)
So your notes are reasonable, but incomplete as they do not define how in some cases the volume is significantly affected as well. Example the horn can be made to move at a speed of 1.1s - faster than sound moves in the air; so upon reaching the observer the newer sounds will be heard very shortly before the older sounds. Not sure how you match up the phases of those – the energy contained in those sounds would not be canceled out by out of phase conditions. Glass breaking sonic booms from real tests show that energy remains very real.
I suppose these could demonstrate characteristics sound has that light does not display; in contrast to the "Transverse Doppler effect" light displays which sound does not.
So Yes your notes look ok, just be alert to faster than sound considerations
Last edited:
gonegahgah
- 376
- 0
That is correct in my opinion Randall; light doesn't use a medium to travel so it can not have the exact equivalent of a sonic boom.
It also tends to mean that light has a greater range on its frequency:
"It's thought that the short wavelength limit is the vicinity of the Planck length, and the long wavelength limit is the size of the universe itself (see physical cosmology), although in principle the spectrum is infinite and continuous." http://en.wikipedia.org/wiki/Electromagnetic_spectrum"
Putting N Normal & H High is a good idea to reduce confusion. You are correct about which ones are which.
I guess you are fairly happy with the results I depict?
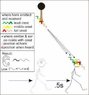
The results show that if the sound emitter moves relative to the air mass then the air mass will draw the note along relative to it but the note gets stretched and lowered in pitch or shortened and increased in pitch due to being pulled away or pushed towards the air mass as it emits.
In the same respect the listener will change the pitch of the sound by moving towards or away from the air mass so that the note shortens and increases pitch as the listener moves towards and through it and it lengthens and decreases pitch as the listener pulls away from the note as it moves through them.
This is all good I hope?
It also tends to mean that light has a greater range on its frequency:
"It's thought that the short wavelength limit is the vicinity of the Planck length, and the long wavelength limit is the size of the universe itself (see physical cosmology), although in principle the spectrum is infinite and continuous." http://en.wikipedia.org/wiki/Electromagnetic_spectrum"
Putting N Normal & H High is a good idea to reduce confusion. You are correct about which ones are which.
I guess you are fairly happy with the results I depict?
The results show that if the sound emitter moves relative to the air mass then the air mass will draw the note along relative to it but the note gets stretched and lowered in pitch or shortened and increased in pitch due to being pulled away or pushed towards the air mass as it emits.
In the same respect the listener will change the pitch of the sound by moving towards or away from the air mass so that the note shortens and increases pitch as the listener moves towards and through it and it lengthens and decreases pitch as the listener pulls away from the note as it moves through them.
This is all good I hope?
Last edited by a moderator:
gonegahgah
- 376
- 0
My apologies Randall; we must have crossed in our answers. Thanks for that reply.
Here are more diagrams showing sound when we are moving in a path that passes in front of the emitter - the path being perpendicular to a direct line to the emitter.
The leftmost diagram (1) shows the horn doing a single honk while the listener moves along the path at half the speed of sound. Although the listener was directly in front of the horn when it honked it takes longer to receive the sound ie. 4 units of time.
The middle diagram (2) shows the horn moving this time while the listener stands still. This time - although the horn is moving - the listener hears the honk in the normal length of time ie. 3 units of time, because the air mass relative to the listener determines how long it takes for them to hear the sound.
The right diagram (3) shows both the horn and air mass moving while the listener is standing still. The sound takes longer to reach the listener ie. 4 units of time, because it is carried with the air mass.
All diagrams depict that the listener hears the same change in pitch. This is because the relative movement between the horn and the user is the same ie. the horn is moving away from the listener at the same angle (or vice versa; it is all relative). The movement of the air mass does not change the pitch.
Again these examples are for sound. Are these diagrams still okay?
Here are more diagrams showing sound when we are moving in a path that passes in front of the emitter - the path being perpendicular to a direct line to the emitter.
The leftmost diagram (1) shows the horn doing a single honk while the listener moves along the path at half the speed of sound. Although the listener was directly in front of the horn when it honked it takes longer to receive the sound ie. 4 units of time.
The middle diagram (2) shows the horn moving this time while the listener stands still. This time - although the horn is moving - the listener hears the honk in the normal length of time ie. 3 units of time, because the air mass relative to the listener determines how long it takes for them to hear the sound.
The right diagram (3) shows both the horn and air mass moving while the listener is standing still. The sound takes longer to reach the listener ie. 4 units of time, because it is carried with the air mass.
All diagrams depict that the listener hears the same change in pitch. This is because the relative movement between the horn and the user is the same ie. the horn is moving away from the listener at the same angle (or vice versa; it is all relative). The movement of the air mass does not change the pitch.
Again these examples are for sound. Are these diagrams still okay?
Attachments
RandallB
- 1,550
- 0
No not for megonegahgah said:
Let's take into account your statement (call them premises)
“because the relative movement between the horn and the user is the same …..(it is all relative). The movement of the air mass does not change the pitch.
In First diagram using the same “relative movement between the horn and the user” before the user past the horn it would be higher not lower. Same relative movement different pitch from different locations. You already said as much in prior diagrams.
Diagram two: Appears to display a transverse perpendicular transfer of sound from horn to user.
I’ve already stated my opinion that sound would not exhibit a "Transverse Doppler effect" and the diagram does not change my opinion of no change in pitch.
Diagram three: I consider evaluated incorrectly – had the horn remained stationary the pitch would have been lower because of the movement of the air contrary to your above premise.
Since the horn is moving away with the wind blowing as shown the pitch would be even lower.
As to: “the horn is moving away from the listener at the same angle” Don’t know you’re driving at; but that angle would never remain the same – and if angle has something significant to do with it (not important to me) these diagrams will not show it.
gonegahgah
- 376
- 0
"user"! Sorry Randall, I'm doing to much programming, lol.
I have to head off shortly so I will look at these further tonight hopefully.
I'm not 100% happy with the diagrams; they do need to be drawn better to show how things would more physically occur.
I just want to quickly look at diagram 2. What will actually happen as the horn moves in its path from the perpendicular point - where the honk begins - is that the honk wave will be dragged out by the horn's sideways movement; just like in the 3rd diagram of the previous 5 direct line examples - except that in that diagram the sound was squashed as the horn and listener are moving directly towards each other and in our new examples they are all moving transversely away. So the wave length would be altered to a lower pitch by the moving horn.
Does that sound better?
What I meant by "angle" is that in each of the three diagrams the horn and listener experience the same relative movement to each other - horn to left in 1st, horn to right in 2nd & 3rd agreed - but still in all the movement is from the perpedicular point and then moves away from that point at the same angle. In my opinion they will all hear the same sound because of this. I will look to diagram and explain this better tonight.
added:
Sorry should mention that the honk occurs at the point where the listener or horn is dotted and is heard where they are solid.
I have to head off shortly so I will look at these further tonight hopefully.
I'm not 100% happy with the diagrams; they do need to be drawn better to show how things would more physically occur.
I just want to quickly look at diagram 2. What will actually happen as the horn moves in its path from the perpendicular point - where the honk begins - is that the honk wave will be dragged out by the horn's sideways movement; just like in the 3rd diagram of the previous 5 direct line examples - except that in that diagram the sound was squashed as the horn and listener are moving directly towards each other and in our new examples they are all moving transversely away. So the wave length would be altered to a lower pitch by the moving horn.
Does that sound better?
What I meant by "angle" is that in each of the three diagrams the horn and listener experience the same relative movement to each other - horn to left in 1st, horn to right in 2nd & 3rd agreed - but still in all the movement is from the perpedicular point and then moves away from that point at the same angle. In my opinion they will all hear the same sound because of this. I will look to diagram and explain this better tonight.
added:
Sorry should mention that the honk occurs at the point where the listener or horn is dotted and is heard where they are solid.
Last edited:
gonegahgah
- 376
- 0
I might go through the diagrams one by one Randall as they take a little time to do.
Here is the leftmost diagram tonight. You can see that I have modified it to more accurately reflect actual physical relativities.
Now it shows the sound wave as it spreads out in three directions. These co-incide with where the listener's ear is when each respective crest of the whole sound wave reaches the listener's ear. The green wave shows the relativity of the front crest of the sound wave, the yellow wave the middle crest, and the red wave the tail crest. Of course sound waves travel as compressions so the listener traveling across the sound will travel across the compressions making them longer or shorter depending upon how they are moving through them.
In our example the listener is moving away from through the compressions so the sound waves are longer to them and lower in pitch. This coincides with where they are as the sound reaches them and their relative direction of movement in relation to the sound.
It appears to me that the resultant wavelength is an addition of the original wave length with how far the listener has traveled between one crest and the next reaching them which will reduce or increase this wavelength.
In our example, where the listener passed beside the horn when it honked, the wavelength continues to get longer as the journey unfolds though the rate slows down as the listener heads off into infinity. This isn't shown super clearly in the diagram but it agrees with the minute measurements from the diagram.
Is this diagram correct now Randall? Can I do anything to improve it?
edit:
Should clarify that "rate slows down" means that the wavelength gets longer more slowly as the journey to infinity continues. The wave length will approach - but not reach - the original wavelength plus the distance traveled for one unit of time at half the speed of sound when the listener reaches towards infinity.
Here is the leftmost diagram tonight. You can see that I have modified it to more accurately reflect actual physical relativities.
Now it shows the sound wave as it spreads out in three directions. These co-incide with where the listener's ear is when each respective crest of the whole sound wave reaches the listener's ear. The green wave shows the relativity of the front crest of the sound wave, the yellow wave the middle crest, and the red wave the tail crest. Of course sound waves travel as compressions so the listener traveling across the sound will travel across the compressions making them longer or shorter depending upon how they are moving through them.
In our example the listener is moving away from through the compressions so the sound waves are longer to them and lower in pitch. This coincides with where they are as the sound reaches them and their relative direction of movement in relation to the sound.
It appears to me that the resultant wavelength is an addition of the original wave length with how far the listener has traveled between one crest and the next reaching them which will reduce or increase this wavelength.
In our example, where the listener passed beside the horn when it honked, the wavelength continues to get longer as the journey unfolds though the rate slows down as the listener heads off into infinity. This isn't shown super clearly in the diagram but it agrees with the minute measurements from the diagram.
Is this diagram correct now Randall? Can I do anything to improve it?
edit:
Should clarify that "rate slows down" means that the wavelength gets longer more slowly as the journey to infinity continues. The wave length will approach - but not reach - the original wavelength plus the distance traveled for one unit of time at half the speed of sound when the listener reaches towards infinity.
Attachments
Last edited:
RandallB
- 1,550
- 0
New Comments & Diagram inculding angle comments still don't make sense to me.
gonegahgah
- 376
- 0
Hi Randall, sorry for my absence. Its taken me some time to nut out the following diagram and other things have been keeping me busy also.
I've looked at my second diagram where the horn is moving (and not the air nor listener) and have seen that it is wrong.
Here is a new diagram. It has three parts: a key, a diagram showing just the horn moving, a diagram showing just the listener and air mass moving.
I've dispensed with showing sine waves on the diagram as I've found it hard to represent the wave showing how the sound compressions move towards the point of hearing. Instead I've replaced it with expanding circles to represent particular crests of the expanding sound compressions. The green expanding circle is the leading compression (or crest), the yellow expanding circle is the middle compression, and the red expanding circle is the rear compression.
I'll explain the key first.
- The dotted figures represent where the actors (horn, listener, air) are at the time the middle crest is emitted ie. t(me) - time middle crest emitted.
- The solid figures represent where the actors are at the time the middle crest is heard ie. t(mh) - time middle crest heard.
Note: where an actor remains stationary the dotted form is hidden by the solid form.
Note: the air is left as invisible so you have to imagine it stationary and moving.
- The green dot shows the point where the lead crest is emitted from and heard at.
- The yellow dot shows the point where the middle crest is emitted from and heard at.
- The red dot shows the point where the rear crest is emitted from and heard at.
Note: where the point of emission or hearing is the same for each crest the green and yellow dot are hidden behind the red dot.
- The little rainbow indicates the early rainbow on the diagrams which show where all the crests are at time t(me) + time for one wavelength to travel ie. t(me) + λ / v(s).
Note: λ is wavelength, v(s) is velocity of sound.
- The crossed green, yellow, red lines indicate where on the diagrams each crest actually meets the ear (at different times of course).
From what I could work out the time each crest would be heard is:
t(mh) = perpendicular distance / v(s)
t(lh) = sqrt( t(mh)^2 + (λ / v(s))^2 ) - λ / v(s)
t(rh) = sqrt( t(mh)^2 + (λ / v(s))^2 ) + λ / v(s)
Note: lh - lead crest heard, mh - middle crest heard, rh - rear crest heard.
t(mh) is fairly obvious because the sound travels at the speed of sound directly along the perpendicular over the distance.
t(lh) & t(rh) both adjust the time of travel by the increased distance of traveling along the hypotenuse from the point of emission to the point of being heard.
Note: the hypotenuse is formed by the time traveled for one wavelength ie. λ / v(s) against the time to travel perpendicular giving: hyp = sqrt( t(mh)^2 + (λ / v(s))^2 ).
t(lh) emitted one wavelength earlier so that time has to be subtracted ie. - λ / v(s).
t(rh) emitted one wavelength later so that times has to be added ie. + λ / v(s).
This means t(lh) will be greater than t(mh) by amount z less difference of emission time,
and t(rh) will be greater than t(mh) by amount z add difference of emission time.
The result is that t(mh) - t(lh) < t(rh) - t(mh) but (t(rh) - t(lh)) / 2 = the normal wavelength.
It means that the sound from before the perpendicular will be higher pitch and the sound from after the perpendicular will be lower pitch.
Note: the amount will be barely noticeable in our example due to the small arc covered. The sound should be fairly normal at the perpendicular for this example.
That is completely different to what I said I know.
With the right diagram I have instead shown the air mass and person moving both at .5v(s) and the horn stationary. In all respects this diagram is basically just a change of perspective upon the first diagram. ie The horn moving and you and the air mass not moving can equally be considered to be you and the air mass moving and the horn not moving. So in all respects the results heard would be the same.
I note that the red and green crest overlap in the right diagram and almost match the yellow crest which is just slightly shorter. If you were to take the three overlapped hearing points (green, yellow, red) from the left diagram, kept them with their matching heard crests and separated the dots by the distance moved in the right diagram this would match how they look in the right diagram. So this would appear to be correct.
Can you study this for me Randall and make sure I have done everything correctly.
I've looked at my second diagram where the horn is moving (and not the air nor listener) and have seen that it is wrong.
Here is a new diagram. It has three parts: a key, a diagram showing just the horn moving, a diagram showing just the listener and air mass moving.
I've dispensed with showing sine waves on the diagram as I've found it hard to represent the wave showing how the sound compressions move towards the point of hearing. Instead I've replaced it with expanding circles to represent particular crests of the expanding sound compressions. The green expanding circle is the leading compression (or crest), the yellow expanding circle is the middle compression, and the red expanding circle is the rear compression.
I'll explain the key first.
- The dotted figures represent where the actors (horn, listener, air) are at the time the middle crest is emitted ie. t(me) - time middle crest emitted.
- The solid figures represent where the actors are at the time the middle crest is heard ie. t(mh) - time middle crest heard.
Note: where an actor remains stationary the dotted form is hidden by the solid form.
Note: the air is left as invisible so you have to imagine it stationary and moving.
- The green dot shows the point where the lead crest is emitted from and heard at.
- The yellow dot shows the point where the middle crest is emitted from and heard at.
- The red dot shows the point where the rear crest is emitted from and heard at.
Note: where the point of emission or hearing is the same for each crest the green and yellow dot are hidden behind the red dot.
- The little rainbow indicates the early rainbow on the diagrams which show where all the crests are at time t(me) + time for one wavelength to travel ie. t(me) + λ / v(s).
Note: λ is wavelength, v(s) is velocity of sound.
- The crossed green, yellow, red lines indicate where on the diagrams each crest actually meets the ear (at different times of course).
From what I could work out the time each crest would be heard is:
t(mh) = perpendicular distance / v(s)
t(lh) = sqrt( t(mh)^2 + (λ / v(s))^2 ) - λ / v(s)
t(rh) = sqrt( t(mh)^2 + (λ / v(s))^2 ) + λ / v(s)
Note: lh - lead crest heard, mh - middle crest heard, rh - rear crest heard.
t(mh) is fairly obvious because the sound travels at the speed of sound directly along the perpendicular over the distance.
t(lh) & t(rh) both adjust the time of travel by the increased distance of traveling along the hypotenuse from the point of emission to the point of being heard.
Note: the hypotenuse is formed by the time traveled for one wavelength ie. λ / v(s) against the time to travel perpendicular giving: hyp = sqrt( t(mh)^2 + (λ / v(s))^2 ).
t(lh) emitted one wavelength earlier so that time has to be subtracted ie. - λ / v(s).
t(rh) emitted one wavelength later so that times has to be added ie. + λ / v(s).
This means t(lh) will be greater than t(mh) by amount z less difference of emission time,
and t(rh) will be greater than t(mh) by amount z add difference of emission time.
The result is that t(mh) - t(lh) < t(rh) - t(mh) but (t(rh) - t(lh)) / 2 = the normal wavelength.
It means that the sound from before the perpendicular will be higher pitch and the sound from after the perpendicular will be lower pitch.
Note: the amount will be barely noticeable in our example due to the small arc covered. The sound should be fairly normal at the perpendicular for this example.
That is completely different to what I said I know.
With the right diagram I have instead shown the air mass and person moving both at .5v(s) and the horn stationary. In all respects this diagram is basically just a change of perspective upon the first diagram. ie The horn moving and you and the air mass not moving can equally be considered to be you and the air mass moving and the horn not moving. So in all respects the results heard would be the same.
I note that the red and green crest overlap in the right diagram and almost match the yellow crest which is just slightly shorter. If you were to take the three overlapped hearing points (green, yellow, red) from the left diagram, kept them with their matching heard crests and separated the dots by the distance moved in the right diagram this would match how they look in the right diagram. So this would appear to be correct.
Can you study this for me Randall and make sure I have done everything correctly.
Attachments
RandallB
- 1,550
- 0
I believe in our prior discussions I had advised that the Light version of your approach demanded that a preferred frame be established and followed by all frames. The traditional SR approach of any reference frame could be used as a preferred frame would not produce the same results. That is you could create descriptions from the view of any of the three reference frames with identical results only if each of those views took only one of the three frames as preferred for defining the correct “Apparent position” of each photon.
Now redoing this same “Apparent position” type of plotting effort for sound requires the same thing.
Only here it should be easier to identify which of the three potential reference frames should correctly be considered “preferred”. As we understand the behavior of sound fairly well, it is well accepted that air is the “ether” for transmitting sound, thus the preferred frame would need to be air.
Your second diagram in the horn frame needs to use “tear drop” shapes to show the correct direction of sound approaching the listener is not the same as the “Apparent path angle” as show by the “Apparent position” plot created for the Horn in its own reference frame.
Said another way the Aberration Angle would depend on the preferred reference frame. That angle of sound impacting the listener as shown in the first diagram needs to be shown as the same in the second diagram. The tear drops would be in-line with the path in the first Air based reference frame. But the tear drops would not be in-line with the path described in your “Apparent position” view as observed by the horn.
IMO the “tear drop” indicator is needed here as well, if your “Apparent Position” method is to be useful. It would be the part of the wave crest that is following the apparent path to the listener.
This would also indicate that apparent paths in-line with tear drops to be “correct” paths in the preferred frame.
As to the wide arch of other sounds going to different locations other than the listener. The depiction shown in the Air Frame seems OK, but what you have displayed in the second view does not appear to be a correct “Apparent position” path for them based on your definition of apparent position.
I’m a little uncertain of what value such a plot might be, but making a proper plot of it might be reveal something useful I’m not thinking of off the cuff right now. You may need a series of three listeners simultaneously working out each straight line case to figure what the apparent position wave front must look like in the Horn reference frame.
Now redoing this same “Apparent position” type of plotting effort for sound requires the same thing.
Only here it should be easier to identify which of the three potential reference frames should correctly be considered “preferred”. As we understand the behavior of sound fairly well, it is well accepted that air is the “ether” for transmitting sound, thus the preferred frame would need to be air.
Your second diagram in the horn frame needs to use “tear drop” shapes to show the correct direction of sound approaching the listener is not the same as the “Apparent path angle” as show by the “Apparent position” plot created for the Horn in its own reference frame.
Said another way the Aberration Angle would depend on the preferred reference frame. That angle of sound impacting the listener as shown in the first diagram needs to be shown as the same in the second diagram. The tear drops would be in-line with the path in the first Air based reference frame. But the tear drops would not be in-line with the path described in your “Apparent position” view as observed by the horn.
IMO the “tear drop” indicator is needed here as well, if your “Apparent Position” method is to be useful. It would be the part of the wave crest that is following the apparent path to the listener.
This would also indicate that apparent paths in-line with tear drops to be “correct” paths in the preferred frame.
As to the wide arch of other sounds going to different locations other than the listener. The depiction shown in the Air Frame seems OK, but what you have displayed in the second view does not appear to be a correct “Apparent position” path for them based on your definition of apparent position.
I’m a little uncertain of what value such a plot might be, but making a proper plot of it might be reveal something useful I’m not thinking of off the cuff right now. You may need a series of three listeners simultaneously working out each straight line case to figure what the apparent position wave front must look like in the Horn reference frame.