paulimerci
- 287
- 47
- Homework Statement
- A boat moves at 8m/s across a river that flows at 2m/s. At what angle must the boat travel so that it moves in a straight line that is perpendicular to the direction of the river's flow?
- Relevant Equations
- Trignometry
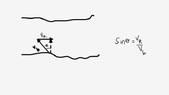
I'm assuming the boat is traveling north at an 8 m/s and the river is flowing east at a 2 m/s. For the boat to move in a straight line, it has to aim at an upstream angle given by #theta#.
Using SOH CAH TOA, ##v_r = 2m/s##, ##v_b = 8m/s##
$$\theta =\sin^{-1} \frac{v_r}{v_b}$$
$$\theta = 14 ~degrees $$
Was the answer right?
Using SOH CAH TOA, ##v_r = 2m/s##, ##v_b = 8m/s##
$$\theta =\sin^{-1} \frac{v_r}{v_b}$$
$$\theta = 14 ~degrees $$
Was the answer right?
Attachments
Last edited by a moderator: