- #1
dl447342
- 28
- 5
- Homework Statement
- A car is driving in a circle of radius R around a banked curve that makes an angle of ##\theta## with the horizontal. If the coefficient of static friction between the cars tires and the road is ##\mu_s##, then what is the maximum speed the car can travel so that it does not slide?
- Relevant Equations
- ##f_s^{\max} = \mu_s n, \sum \vec{F} = m \vec{a}, a = mv^2/R.##
Here's a FBD I made for this question.
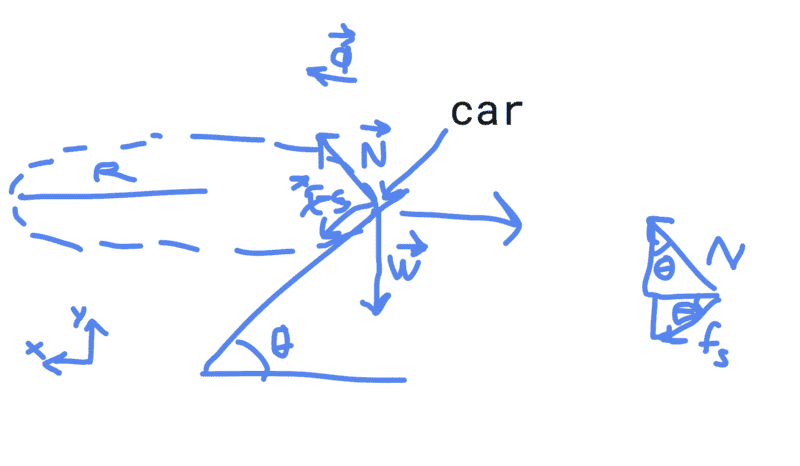
From the diagram, I obtained that ##-W + N \cos\theta - f_s \sin\theta = 0##. And ##N\sin\theta + f_s \cos\theta = ma = \frac{mv^2}{R} \leq N\sin\theta + f_s^{\max} \cos\theta = \frac{mv_{\max}^2}{ R}##. Solving these equations, and using the angle addition formula for tan, I get ##v_{\max} = \sqrt{gR \tan (\theta + \theta_s)}##. If ##\theta_s## satisfies ##\mu_s = \tan \theta_s## and ##\theta > 90^{\circ} - \theta_s,## then ##tan (\theta + \theta_s) < 0,## so maybe ##v_{\max} = \infty##? And if so, why? Is it because in that case ##f_s(1-\mu_s \tan\theta) \leq \mu_s W## is always true so that ##f_s^{\max} = \infty##? Btw, I got the latter inequality by using the fact that ##f_s^{\max} = \mu_s N## and the very first equation; the first equation gives ##f_s = \frac{N\cos\theta - W}{\sin\theta}## and this is at most ##\mu_s N =\frac{ \mu_s (W + f_s\sin\theta)}{\cos\theta} \Rightarrow f_s (1-\mu_s \tan\theta) \leq \mu_s \frac{W}{\cos\theta}##.
From the diagram, I obtained that ##-W + N \cos\theta - f_s \sin\theta = 0##. And ##N\sin\theta + f_s \cos\theta = ma = \frac{mv^2}{R} \leq N\sin\theta + f_s^{\max} \cos\theta = \frac{mv_{\max}^2}{ R}##. Solving these equations, and using the angle addition formula for tan, I get ##v_{\max} = \sqrt{gR \tan (\theta + \theta_s)}##. If ##\theta_s## satisfies ##\mu_s = \tan \theta_s## and ##\theta > 90^{\circ} - \theta_s,## then ##tan (\theta + \theta_s) < 0,## so maybe ##v_{\max} = \infty##? And if so, why? Is it because in that case ##f_s(1-\mu_s \tan\theta) \leq \mu_s W## is always true so that ##f_s^{\max} = \infty##? Btw, I got the latter inequality by using the fact that ##f_s^{\max} = \mu_s N## and the very first equation; the first equation gives ##f_s = \frac{N\cos\theta - W}{\sin\theta}## and this is at most ##\mu_s N =\frac{ \mu_s (W + f_s\sin\theta)}{\cos\theta} \Rightarrow f_s (1-\mu_s \tan\theta) \leq \mu_s \frac{W}{\cos\theta}##.
Attachments
Last edited:
