NascentOxygen
Staff Emeritus
Science Advisor
Homework Helper
- 9,249
- 1,080
That's the right idea. But because of the presence of the resistor, the inductor must develop a bit more than 65V. Some of its voltage is dropped across the resistor, to leave 65V for the neon.Jay_ said:So let me see if I got this right. If V = L(di/dt) and the switching is instant, so the inductor will try to reach infinite voltage. But the neon gives the voltage a path to flow when it reaches 65, and so the voltage build up on the inductor stops? Would that be right?
Yes, unless it is a superconductor. The particular value of resistance is determined by many factors, including the characteristics of the neon. The resistor is not crucial, but the neon may be damaged if the current is not limited to a value it is designed for. If you were worried, you could leave out the neon and let the spark jump across a narrow air gap between two wires.Even a coil has some resistance right? So what I was asking is: Is there a particular resistance value (a minimum) for this condition of "dumping all its energy in a brilliant flash" to not happen?
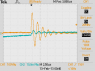
I'm hoping you are about ready to sketch the waveform (current versus time) of the current in the inductor. The task is already half done for you: in the original video they have sketched the current as it builds up while driven by the battery. Now all you have to do is sketch the current as it winds back down to zero. Don't worry about getting the time scale exact, because you can't. We don't know the value of L or R, so it becomes a generalized sketch.