Block on an accelerating wedge (part c only)

[AspiringPhysicist12]

Homework Statement

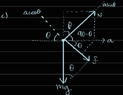
A block rests on a wedge inclined at angle θ. The coefficient of friction between the block and plane is μ.

(b) The wedge is given horizontal acceleration a, as shown.
Assuming that tan θ > μ, find the minimum acceleration for the
block to remain on the wedge without sliding.

(c) Repeat part (b), but find the maximum value of the acceleration.

Relevant Equations

mgsin(theta) + f = macos(theta)
N - mgcos(theta) = masin(theta)

I have to use the inertial frame only.

My solution for part b) (i.e. minimum acceleration) in case it's needed: https://ibb.co/D8CCQMM

I'm confused about part c.

1) Since the block will travel up the incline if a > a_max, acos(theta) is up the incline. But based on my attached FBD diagram, acos(theta) should be down the incline, not up it, if the acceleration a is to the right.

2) Also, my FBD diagram I attached suggests that the block will travel up the incline if a > a_max. But the only forces acting on the block are the normal force, gravity, and friction; none of which have a component up the incline that would cause the block to move in that direction. So what am I missing here?

 

[Lnewqban]

The resistive reaction to that slope acceleration is what balances the forces trying to slide the block down the slope.

 

[kuruman]

If left alone, the block will accelerate down because the angle of the incline is greater than the angle of repose.
If the incline is accelerated, the block's acceleration will diminish until it goes to zero. At that point the block is at the threshold of just barely sliding down.
If the incline is acceleration is increased past that first threshold, the block will be at rest relative to the incline until the incline's acceleration reaches a value at which the block will be just at the second threshold of sliding up.

The acceleration at the second threshold is the maximum you are looking for. Draw an FBD noting that the force of static friction points in the opposite direction from the first threshold direction. It follows that for some block acceleration in between the two threshold values, the force of static friction is zero. That is the acceleration at which the block will be stationary relative to a frictionless accelerating incline.

 

[AspiringPhysicist12]

Ok, thank you for the replies, now I just want to confirm. In a frame of reference moving with the wedge, the block has a psuedoforce ma to the left which provides a component pointing up the incline. If macos(theta) > mgsin(theta) + f, then the block will travel upwards.

But in an inertial frame of reference, we attribute the ball's tendency to go up the incline to inertia rather than to any specific force, right? I know the math works out the same regardless of frame.

 

[PeroK]

But in an inertial frame of reference, we attribute the ball's tendency to go up the incline to inertia rather than to any specific force, right?

In an inertial frame of reference, Newton's laws apply and there must be a net upwards force if the block is accelerating upwards.

That force comes from the contact with the wedge. And, in particular, the vertical component of the normal force.

 

[Lnewqban]

...
But in an inertial frame of reference, we attribute the ball's tendency to go up the incline to inertia rather than to any specific force, right? I know the math works out the same regardless of frame.

Think of forces and accelerations on the block for both extreme situations, angle of slope being 0 and 90.
Our situation is somewhere in between those two.

 

[AspiringPhysicist12]

Thanks guys, I think I get what you mean physically but when I draw the free body diagram, it just doesn't make sense. Could you check my diagram for a > a_max and tell me if there's anything wrong with it?

https://ibb.co/wg79Ck7

I have 2 main concerns that I would appreciate if you could address separately.

1) Since the normal force is perpendicular to the wedge, it does not have a component parallel to the wedge, and so I don't see how it can cause the block to move upwards parallel to the incline. This leaves us with friction and gravity; both of which point down the incline and not up it.

2) If the block has a tendency to move up the incline for a > a_max, then since ma is the net force, I feel that macos(theta) should point up the incline and not down it. But if the acceleration a is to the right, then the components won't make sense. This is what I mean:

https://ibb.co/rbgwVHn

Sorry for all these stupid questions by the way, it's just really bothering me.

 

[Lnewqban]

Think of the block and the Earth only, forget about the wedge for now.
Any string attached to the right side of the block could transfer the horizontal force that causes acceleration a towards the right.

That induces a reaction horizontal force at the attachment point.

Now, the surface of the edge is constraining the direction of the block’s freedom of movement under the action of a net force.

 

[PeroK]

Thanks guys, I think I get what you mean physically but when I draw the free body diagram, it just doesn't make sense. Could you check my diagram for a > a_max and tell me if there's anything wrong with it?

https://ibb.co/wg79Ck7

I have 2 main concerns that I would appreciate if you could address separately.

1) Since the normal force is perpendicular to the wedge, it does not have a component parallel to the wedge, and so I don't see how it can cause the block to move upwards parallel to the incline. This leaves us with friction and gravity; both of which point down the incline and not up it.

In the ground frame, the block is always moving up and in the direction of the wedge's acceleration. Its motion is only parallel to the wedge in the wedge's frame where fictitious forces apply.

2) If the block has a tendency to move up the incline for a > a_max, then since ma is the net force, I feel that macos(theta) should point up the incline and not down it. But if the acceleration a is to the right, then the components won't make sense. This is what I mean:

https://ibb.co/rbgwVHn

Sorry for all these stupid questions by the way, it's just really bothering me.

Again, the direction "up the incline" is not correct in the ground frame.

In the wedge frame, the fictitious force on the block is to the left, which decomposes into a normal force into the wedge and a force up the incline of the wedge.

Bascically, if you push something into a hill it goes up the hill. Which is the same as the hill being pushed into it.

 

[jbriggs444]

Since the normal force is perpendicular to the wedge, it does not have a component parallel to the wedge, and so I don't see how it can cause the block to move upwards parallel to the incline.

If you are using a reference frame, use the reference frame.

Inertial frame:

In your drawing, we are considering a rightward-accelerating wedge. In the inertial frame the block is not accelerating diagonally leftward. It is accelerating diagonally rightward. There is no need to explain a leftward acceleration because there is no leftward acceleration.

Wedge-centered frame:

Now we have a block accelerating diagonally leftward parallel to the face of the wedge. And there is a pseudo-force to explain the acceleration.

 

[kuruman]

If you are using a reference frame, use the reference frame.

Inertial frame:

In your drawing, we are considering a rightward-accelerating wedge. In the inertial frame the block is not accelerating diagonally leftward. It is accelerating diagonally rightward. There is no need to explain a leftward acceleration because there is no leftward acceleration.

Wedge-centered frame:

Now we have a block accelerating diagonally leftward parallel to the face of the wedge. And there is a pseudo-force to explain the acceleration.

I don't understand why you say that the block is accelerating diagonally in either frame. The problem specifies that the block remains on the wedge without sliding. This can only mean that the block and the wedge move as one with the same horizontal acceleration. If you are treating the general case where the block is sliding relative to the wedge, why bother?

 

[jbriggs444]

I don't understand why you say that the block is accelerating diagonally in either frame. The problem specifies that the block remains on the wedge without sliding. This can only mean that the block and the wedge move as one with the same horizontal acceleration. If you are treating the general case where the block is sliding relative to the wedge, why bother?

OP is wondering how upward sliding could occur. So it seems appropriate to consider how upward sliding could occur.

 

[AspiringPhysicist12]

Thank you so much, everyone! I didn't realize the block only has a net acceleration up the incline in the non-inertial frame, but that solves all of my confusions.