Thermofox
- 144
- 26
- Homework Statement
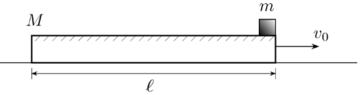
- A wooden slab, with a mass of ##M = 80 kg##, initially moves with an uniform rectilinear motion, on a horizontal surface devoid of friction. The slab has a velocity ##v_{s,i}=6 m/s##. At a certain instant, a block, assumed to be a point mass with a mass of ##m = 12 kg##, is placed on the right end of the slab. The block initially has a velocity of zero, relative to a frame of reference fixed to the horizontal surface. Knowing that there is a frictional force characterized by the coefficient of kinetic friction ##μ_k= 0.3## between the slab and the block, determine:
1) the minimum length of the slab such that the block does not fall from it;
2) assuming that now the length is ##l \gt l_{min}##. Determine the time that elapses from when the block is left on the slab and the instant the two bodies will move together.
- Relevant Equations
- ##\Delta E_m = 0## ##\Delta P = 0##
For the first question I thought of using an energy balance,
there is friction ##\Rightarrow \Delta E_m = -W_f##. Both at the start and at the end, the block has no velocity. Therefore ##E_{\text{initial}}= \frac 1 2 m_s v_{s,i}^2## and ##E_{\text{final}}= \frac 1 2 m_s v_{s,f}^2##. This means that: $$\frac 1 2 m_s v_{s,f}^2 - \frac 1 2 m_s v_{s,i}^2 = \mu_k m_b g l_{min}$$ From this I can determine ##l_{min}##, but first I need to find a relationship to define ##v_{s,f}##.
That's where I'm stuck at. I tried considering the system as a whole. This means that there is conservation of linear momentum, hence:
##\Delta P = 0 ;P_{\text{final}} - P_{\text{initial}} = 0##. The problem is that ##P_i = m_s v_{s,i}## and ##P_f= m_s v_{s,f}##. This means that the slab maintains the same velocity, but that doesn't make sense. So there must be an error, but I can't see it.
Furthermore, for question 2, since I have to determine time, I think I need to use kinematic. Can I assume that the block moves with an uniform acceleration?
there is friction ##\Rightarrow \Delta E_m = -W_f##. Both at the start and at the end, the block has no velocity. Therefore ##E_{\text{initial}}= \frac 1 2 m_s v_{s,i}^2## and ##E_{\text{final}}= \frac 1 2 m_s v_{s,f}^2##. This means that: $$\frac 1 2 m_s v_{s,f}^2 - \frac 1 2 m_s v_{s,i}^2 = \mu_k m_b g l_{min}$$ From this I can determine ##l_{min}##, but first I need to find a relationship to define ##v_{s,f}##.
That's where I'm stuck at. I tried considering the system as a whole. This means that there is conservation of linear momentum, hence:
##\Delta P = 0 ;P_{\text{final}} - P_{\text{initial}} = 0##. The problem is that ##P_i = m_s v_{s,i}## and ##P_f= m_s v_{s,f}##. This means that the slab maintains the same velocity, but that doesn't make sense. So there must be an error, but I can't see it.
Furthermore, for question 2, since I have to determine time, I think I need to use kinematic. Can I assume that the block moves with an uniform acceleration?