russ_watters
Mentor
- 23,706
- 11,151
Here is a selection for the highest pressure blower you're likely to find:
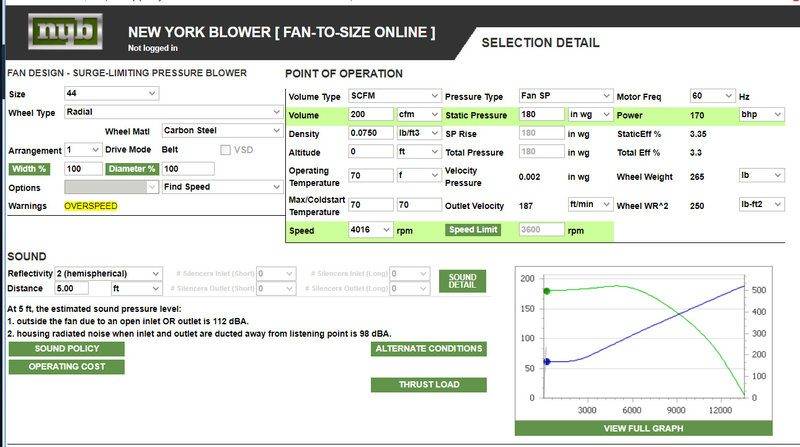
180 inches of water gauge is 6.5 psi or an available pressure ratio of 0.69. That's a lot better than I would have expected, but still quite a bit above the maximum required for choked flow of <0.5. And it requires 170 horsepower for just 200SCFM of airflow. That's like a midsized car engine at full throttle to run a bathroom fan.
180 inches of water gauge is 6.5 psi or an available pressure ratio of 0.69. That's a lot better than I would have expected, but still quite a bit above the maximum required for choked flow of <0.5. And it requires 170 horsepower for just 200SCFM of airflow. That's like a midsized car engine at full throttle to run a bathroom fan.
Attachments
Last edited:




