user079622
- 449
- 29
- Homework Statement
- I stuck at beginning ,due to wrong reasoning. I need better explanation.
- Relevant Equations
- F=ma
M=Fxd
a=ω2r
I want to calculate center of rotation for monocopter, from inertial reference frame,earth.
One case when fly in the air in one steady height/place and second case is in free space,then has rocket engine instead fan.
I draw forces what I think that must exist.
m=2kg
Ft(thurst)= 100N
ω=500RPM
Can I find center with this data or I need more informations?
Axioms:
Space case
(I am in space station near the stick wich is at rest, then I start rocket engine of stick and observing, neglect loss in fuel mass)
I have only one force and mass, so I know Fnet must be non zero.I know that CoM will not accelerate in straight line, because force dont going through CoM.
I also know that object cant rotate around CoM because of Fnet is non zero .
So Fnet is non zero implies, that CoM must orbit around some point but I don have centripetal force for this movement
I am stuck in my contradictions, obviously my reasoning is wrong because physics laws must be true.
What I am doing wrong?
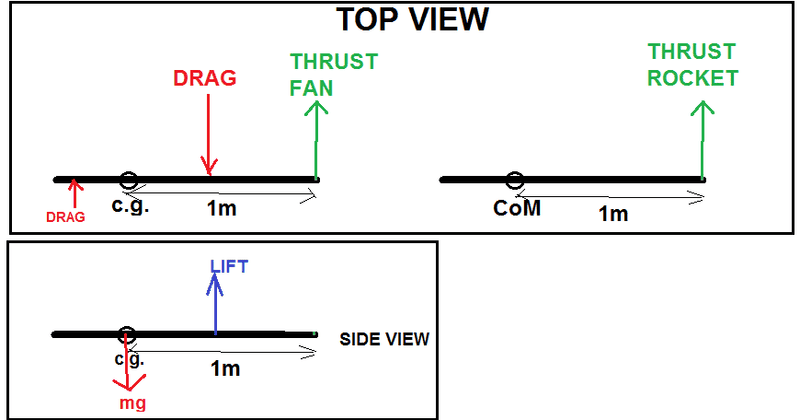

One case when fly in the air in one steady height/place and second case is in free space,then has rocket engine instead fan.
I draw forces what I think that must exist.
m=2kg
Ft(thurst)= 100N
ω=500RPM
Can I find center with this data or I need more informations?
Axioms:
- A pure force thorugh the center of mass (with no net torque about the center of mass) will purely translate a rigid body (any point on the body).
- A pure torque any point on the body (with no net force) will purely rotate a rigid body about its center of mass.
Space case
(I am in space station near the stick wich is at rest, then I start rocket engine of stick and observing, neglect loss in fuel mass)
I have only one force and mass, so I know Fnet must be non zero.I know that CoM will not accelerate in straight line, because force dont going through CoM.
I also know that object cant rotate around CoM because of Fnet is non zero .
So Fnet is non zero implies, that CoM must orbit around some point but I don have centripetal force for this movement
I am stuck in my contradictions, obviously my reasoning is wrong because physics laws must be true.
What I am doing wrong?
Last edited: