GVdig
- 3
- 0
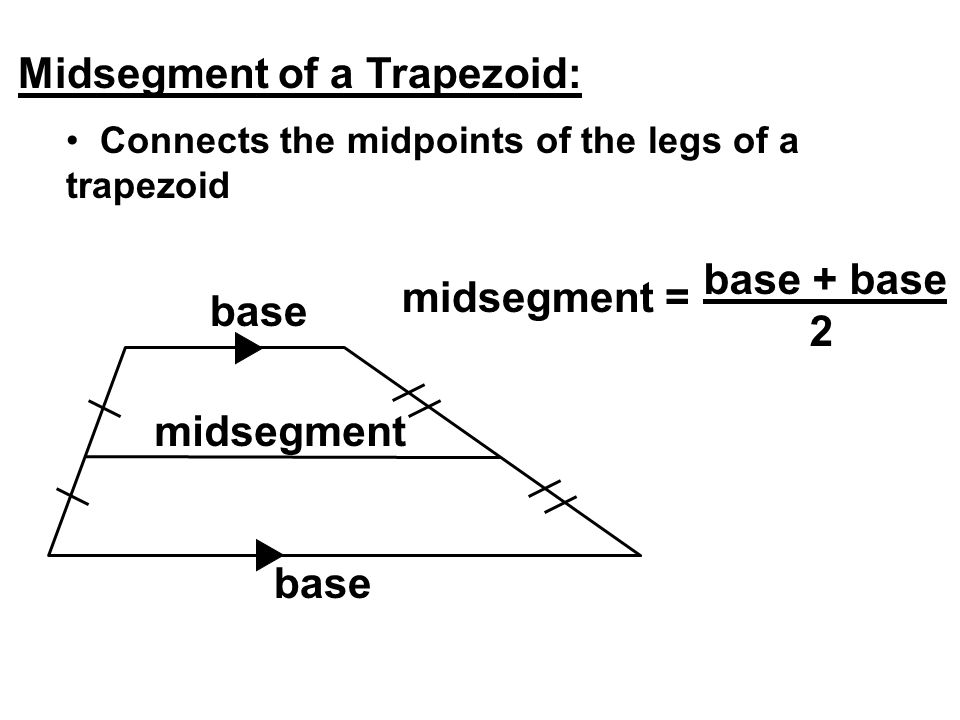
The two non-parallel sides of the trapeze are 15 cm and 13 cm, the perimeter is 48 cm. Find the length of the median.
I don't know anything about trapezes can someone expain how to do this?
View attachment 8192
I don't know anything about trapezes can someone expain how to do this?
View attachment 8192