SuperCat
- 26
- 1
Note: I have come up with a solution myself, but I am trying to understand a different approach to the problem. My textbook solves it in a different manner, and I am having trouble following along.
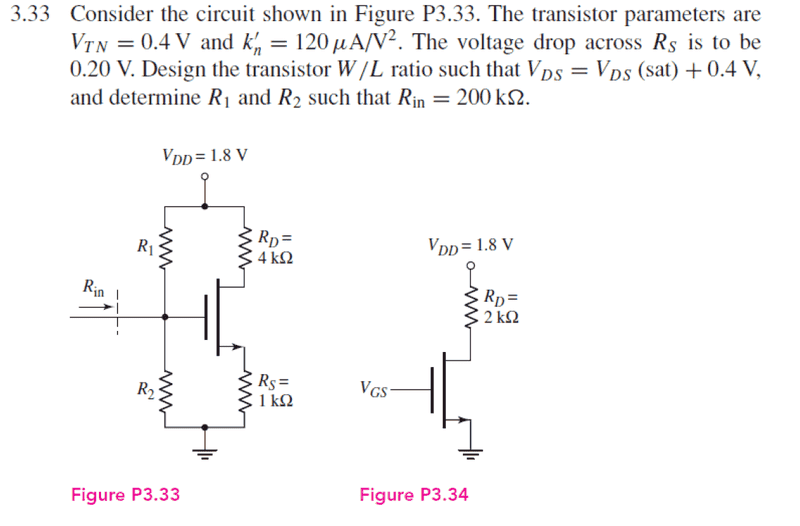
The last part of the problem "determine R1 and R2 such that Rin = 200k". I am having trouble understanding the solution for it. Note the graph for the problem is on the left.
Ohm's law and KVL.
Solution provided to me:
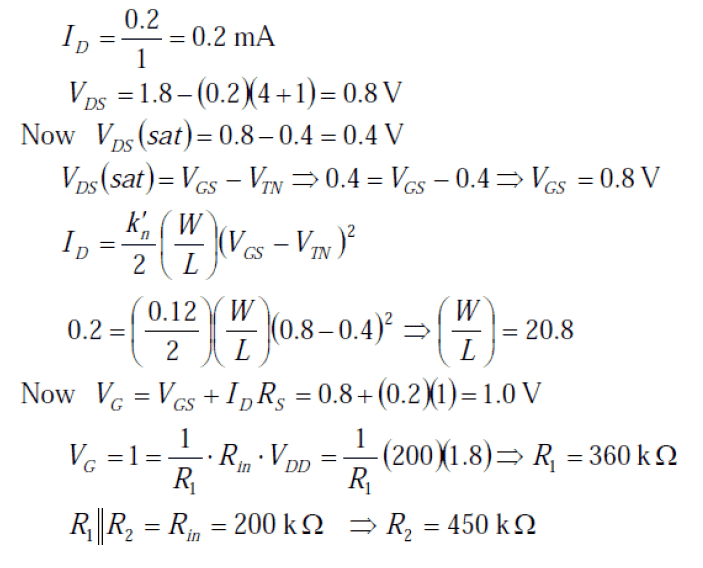
The solution for the resistance starts towards the bottom, once the gate voltage has been calculated. I do not understand why that formula is used to solve for the first resistor. To me it looks like conductance of the first resistor is being used with the Vdd to get a current. That current is being multiplied by the equivalent thevinin resistance of the two resistors. I just don't understand why that would be useful/how that would lead to calculating the resistance.
Homework Statement
The last part of the problem "determine R1 and R2 such that Rin = 200k". I am having trouble understanding the solution for it. Note the graph for the problem is on the left.
Homework Equations
Ohm's law and KVL.
The Attempt at a Solution
Solution provided to me:
The solution for the resistance starts towards the bottom, once the gate voltage has been calculated. I do not understand why that formula is used to solve for the first resistor. To me it looks like conductance of the first resistor is being used with the Vdd to get a current. That current is being multiplied by the equivalent thevinin resistance of the two resistors. I just don't understand why that would be useful/how that would lead to calculating the resistance.
Last edited: