Calculate the angular velocity of the milk carton

[javii]

Homework Statement

Homework Equations

The Attempt at a Solution

Is it correct?

 

[kuruman]

Is it correct?

No. You need to use the moment of inertia about the corner of the carton and you need to find the correct height of the center of mass when tipping occurs.

 

[berkeman]

Maybe this problem does not intend to involve the full complexity of this situation, but milk cartons are not "full" of liquid, even when new. The movement of the liquid inside the carton would need to be accounted for in a full solution, IMO.

 

[kuruman]

The movement of the liquid inside the carton would need to be accounted for in a full solution, IMO.

That is true, but since no mention is made in the problem about liquid in the carton, we may assume that it is empty. It could an empty carton on a cafeteria conveyor belt on its way to the trash disposal area.

On edit: Of course, the moment of inertia of an empty carton is more complicated to calculate.

 

[haruspex]

Maybe this problem does not intend to involve the full complexity of this situation, but milk cartons are not "full" of liquid, even when new. The movement of the liquid inside the carton would need to be accounted for in a full solution, IMO.

It's also an issue for cartons that are full. The milk would tend to rotate internally in the opposite direction.
But an earlier part of the question says to ignore any sloshing around https://www.physicsforums.com/threads/calculate-the-maximum-acceleration-of-a-milk-carton.911818/.

There is another complication. Is it easily shown that the carton does not lose contact with the ground?

 

[javii]

No. You need to use the moment of inertia about the corner of the carton and you need to find the correct height of the center of mass when tipping occurs.

So, the formula i have to use is:
1/3*m*(b^2+l^2)?

and when i use that one i get

which leads me to:

so the angular velocity is 9.15 rad/s ?

 

[haruspex]

So, the formula i have to use is:
1/3*m*(b^2+l^2)?

and when i use that one i get
View attachment 196008

Why are you dividing the 0.195 by 2 but not the 0.07?

 

[kuruman]

which leads me to:

And why do you think the CM is at height $\frac{0.195}{2}~m$ just before the carton tips over? That's its height when the carton sits flat on the conveyor belt.

 

[javii]

Why are you dividing the 0.195 by 2 but not the 0.07?

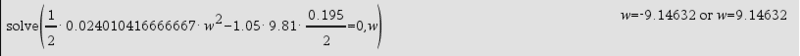
For me, it is obvious that I have to divide 0.195 with 2, but I am not sure if 0.07 also have to be divided with 2 since the carton is
skewed.
So your are saying, that I also have to divide 0.07 with 2?

 

[kuruman]

So your are saying, that I also have to divide 0.07 with 2?

Yes, but it is important to understand why. Start with $I_{CM}=\frac{1}{12}M(l^2+a^2)$ and apply the parallel axes theorem. Try using symbols, not numbers. What do you get?

 

[javii]

Yes, but it is important to understand why. Start with $I_{CM}=\frac{1}{12}M(l^2+a^2)$ and apply the parallel axes theorem. Try using symbols, not numbers. What do you get?

I_p= 1/12M(l^2+a^2)+M+d^2

I_p=1/12M*l^2+1/12*a^2+M+d^2 ?

 

[javii]

And why do you think the CM is at height $\frac{0.195}{2}~m$ just before the carton tips over? That's its height when the carton sits flat on the conveyor belt.

I see, it is a mistake by me. Its just the height.
Thanks

 

[haruspex]

I_p= 1/12M(l^2+a^2)+M+d^2

I_p=1/12M*l^2+1/12*a^2+M+d^2 ?

I assume you mean Md², not M+d².
What is d² in terms of l and a?

 

[haruspex]

I see, it is a mistake by me. Its just the height.
Thanks

So what do you get now for the vertical displacement of the mass centre?