Calculate the radius of the circle

[Help seeker]

A, B and C are points on a circle with center O. Angle ABC = $75°$ . The area of the shaded segment is $200cm^2$ .

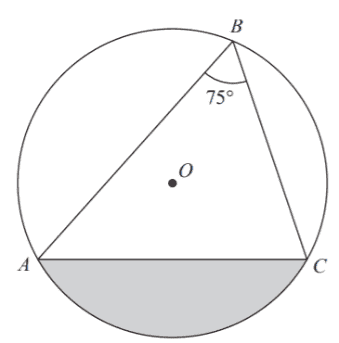
Calculate the radius of the circle. Answer correct to $3$ significant figures.

 

[Opalg]

What is the angle AOC? In terms of $r$ (the radius of the circle), what is the area of the triangle AOC? What is the area of the sector AOC of the circle? The difference between those last two areas is the area of the shaded segment. That should give you an equation for $r$.

 

[HOI]

An angle with vertex on a circle cuts that circle in an arc with measure twice the measure of the angle. And an angle with vertex at the center of the circle cuts that circle in an arc with measure equal to the angle. Here angle ABC has measure 75 degrees so arc AC and angle AOC have measure 150 degrees. Knowing that, you can find the areas of segment AOC and triangle AOC as functions of r, the radius of the circle, Subtract those to areas to find the area of the gray region as a function if r, set that equal to 200, and solve for r.

 

[HOI]

Since this has been here a while:
Sector AOC is 150/360= 15/36= 5/12 of the entire circle, The entire circle has area $\pi r^2$ so sector AOC is $5\pi r^2/12$. Triangle AOC is an isosceles triangle with two sides of length r and vertex angle 150 degrees. An altitude of triangle AOC bisects angle AOC so divides triangle AOC into two right angles with hypotenuse of length r and one angle 150/= 75 degrees. The "near side", the altitude, has length h= r cos(75) and the "opposite side", half of AC, has length b= r sin(75). All of AC, the base of triangle AOC, has length 2r sin(75) so triangle (1/2)hb= r^2 sin(75)cos(75).

So the shaded segment has area $\frac{5\pi r^2}{12}- r^2sin(75)cos(7)= \left(\frac{5\pi r^2}{12}- sin(75)cos(75)\right)r^2$.

 

[Help seeker]

Tnx.
SOLVED

 

[jonah1]

Brandy induced ramblings follow.

...
So the shaded segment has area $$\frac{5\pi r^2}{12}- r^2sin(75)cos(7)= \left(\frac{5\pi r^2}{12}- sin(75)cos(75)\right)r^2$$

Minor typo.
That should have been
$$\frac{5\pi r^2}{12}- r^2sin(75)cos(75)= \left(\frac{5\pi}{12}- sin(75)cos(75)\right)r^2$$