- #1
cuz937100
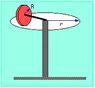
A toy gyroscope consists of a M = 2.5 kg disk with a radius of R = 2 cm mounted at the end of a light axle r = 7 cm long. The gyroscope spins at f = 47 rev/s. It is held horizontal at one end of its axle and precesses about its stand as shown.
a) What is the angular momentum of the disk about its axle?
b) What is the torque about the point of support due to the weight of the gyro?
c) How long does it take the gyroscope to precess once around?
d) If the radius of the disk and the length of the axle were both doubled (R = 4 cm, r = 14 cm), and the rate at which the disk spins were kept the same, how long would it take the disk to precess once?
I have figured out parts a and b (a.0.148,b.1.72), and I thought that part c would just be the inverse of (part b/part a)(Torque/Angular Momentum) due to the fact that angular precesion is just a frequency meaning the inverse would be the period. This did not work and I can not figure out part d without part c. Can someone please help me with this problem? There is a pic of it attached...
a) What is the angular momentum of the disk about its axle?
b) What is the torque about the point of support due to the weight of the gyro?
c) How long does it take the gyroscope to precess once around?
d) If the radius of the disk and the length of the axle were both doubled (R = 4 cm, r = 14 cm), and the rate at which the disk spins were kept the same, how long would it take the disk to precess once?
I have figured out parts a and b (a.0.148,b.1.72), and I thought that part c would just be the inverse of (part b/part a)(Torque/Angular Momentum) due to the fact that angular precesion is just a frequency meaning the inverse would be the period. This did not work and I can not figure out part d without part c. Can someone please help me with this problem? There is a pic of it attached...
Attachments
Last edited by a moderator: