Calculating area of multiple connected circles

[magnetics]

Hopefully this is a challenging maths problem for someone. This problem is to compare the surface area of the 4 identical circles with the circle overlayed drawn in pencil.

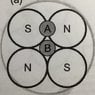
The attached image shows 4 circles, each with diameter x.
To solve the problem, I need to calculate the maximum separation between the circles represented by the circle B with diameter B.

Once B can be calculated, 2x + B will be the diameter of a single circle overlayed over the four as shown in pencil.

This seems to me to be the simplest method to compare the difference in surface area between the four circles and the overlayed circle
i.e. the four circles -> πx²
and the overlayed circle -> π(x+B/2)²

Or there maybe an easier way I have overlooked??

Thank you.

NOTE:
The surface area of the four circles uses the formula πr², but where r = x/2 and for four identical circles is 4 x π(x/2)² which is 4πx²/4 which is πx²

Sorry if I'm not very familiar with using the correct symbols on this platform.

 

[mfb]

Make a triangle with the centers of two "S" circles and one "N" circle (or vice versa), and you'll find a method that is much easier than area calculations.

 

[magnetics]

Right you are mfb.
Thank you!