negation
- 817
- 0
BvU said:Hello negation. Appreciate your hard work. You 've got most of it but the ciphering creates mist and confusion. I don't think a little help is a spoiler at this point:
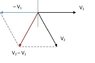
In your picture in #14 you have two vectors: v2 and v1. Draw them again in a new picture, where both grab at the origin. The angle between them is known, right? (Hint: don't use a calculator. Numbers like 0.523 -- which you later corrected to 1.047197551... -- are a lot less helpful than numbers like π / 3). Draw -v1 and then v2 + (-v1). That is the change in the speed vector in 5 minutes. Note it is a vector and it doesn't point downwards. The magnitude is evident. Divide by 5 minutes and you get the average acceleration vector. Its length is π m/min2. (Exactly. The 8.73... is only an approximation for π/3600. On the other hand, vela's 10-5 seems to be a typo to me, so your -4 is better...).
If you want to learn something, repeat the exercise for 1 minute instead of 5 and so on, all the way to dt = 0. If all is well, you just might end up with the 9.138 * 10-4. Or, more correctly ω2 r being π2/3 m/min2.
Don't let the hard work of calculating distract you from the insight: the instantaneous acceleration and the average acceleration are quite different beasts!
You'll know you understand it completely if you can swing a small weight at the end of a rope: what do you do to get it to go in a circle and what do you do to keep it circling...
I have no problem spending days solving a problem. My life revolves around physics and math. I'm not satisfied leaving a problem unsolved. But indeed, this question is a real pain mainly because the definition of the terms comes across as rather chaotic to me.
the question asked about average acceleration, can I presume that are asking about [tangential velocity 2 - tangential velocity 1]/300s? What I am also confused is with the [v2+(-v1)]/300s that you stated. Why is there a negative?
As to your question, what do you mean by grab at the origin? I presume you meant for the radius to extends from (0,0)?
At t=0, my radius points straight north with tangential velocity 1 perpendicular to the radius and at t=300s, my radius points at 12.05 with tangential velocity 2 at perpendicular to this radius. The difference in radians between the radius is 1.05... Or pi/3 as you put it.
This change in angle is in similar ratio to the change in angle between the 2 tangential velocity vector.
This is based on the premise
delta r / r = delta v/v.
Am I right with the above? If I am, I will proceed to work further.