cloned33
- 3
- 0
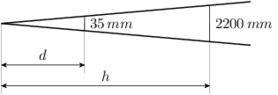
Hello,just seeing if someone can help me on here,i have a rc glider measuring 2200 mm on the ground,when in the air it measures about 35mm. Can the the height be calculated from these measurements.