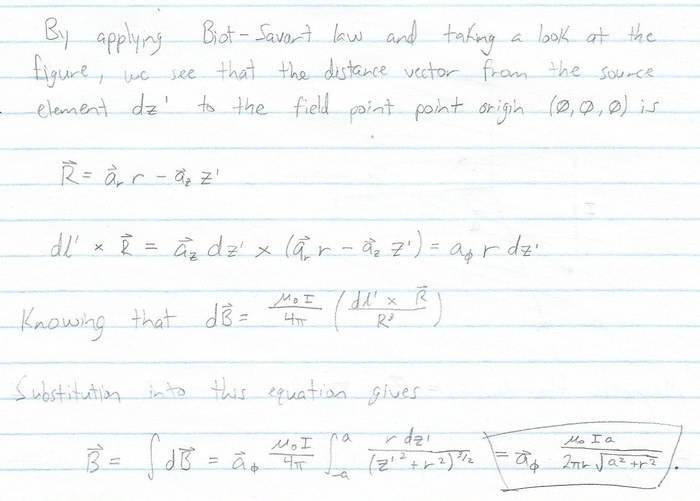mfb said:
What is r, why do you consider z if everything happens in the x/y plane? Where does the expression for ##\vec{R}## come from?
In particular, how can your result depend on "r" which does not appear in the problem statement? The direction of the answer does not seem to make sense - how can something at the origin point in the direction of an angle?
Did you try to use cylindrical coordinates? I don't think that helps.
I don't understand why you integrate from -a to a.
I think you forgot to multiply the final result by 3 for the three wires, but there are several other things to fix first.
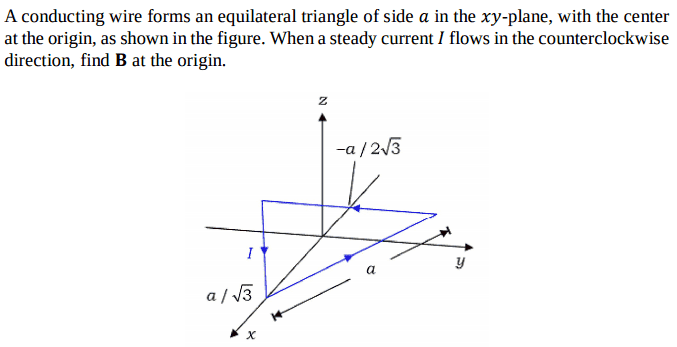
You are correct. Neither d
l nor
R should have components along
ez. Since the triangle lies in the x-y plane (z=0), d
l should have components along
ex and
ey. Also,
R should only have components along
ex and
ey because it's pointing from the location of d
l , which is in the x-y plane, to the origin, which is also in the x-y plane. Accordingly, the cross product d
l x
R would come out to be along
ez, which is what we should expect from the right hand rule.
I am having a hard time computing d
l and
R. When I find d
l and
R it's a simple substitution into d
B from there. Could you show me how you would calculate d
l and
R ?