Guillem_dlc
- 188
- 17
- TL;DR Summary
- How is the mass inertia product calculated? I have two examples and each one uses something different.
How is the mass inertia product calculated? I have two examples and each one uses something different.
Example 1:

Example 2: moments and product of inertia of the cylinder
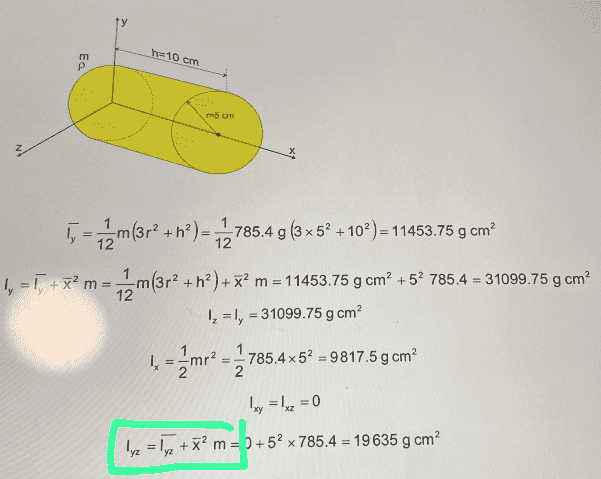
Example 1:
Example 2: moments and product of inertia of the cylinder