Nate Learning
- 2
- 0
We have this picture and the questing is:
What is the probability the tile is worth 3
points given the tile is a consonant?
and
A player selects two tiles blindly without replacement. What is the probability the
second tile is a vowel given the first tile is a consonant?
Is this like the Urn example with ball replacement? would I solve it the same way? any examples would be nice. Thank you
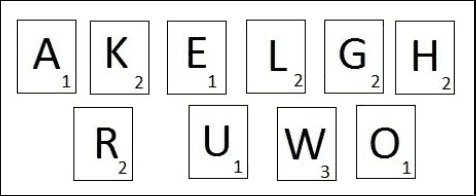
What is the probability the tile is worth 3
points given the tile is a consonant?
and
A player selects two tiles blindly without replacement. What is the probability the
second tile is a vowel given the first tile is a consonant?
Is this like the Urn example with ball replacement? would I solve it the same way? any examples would be nice. Thank you