yilbaris
- 6
- 0
Hi, i have a question..
I need to make a "bumper project" as shown in figure.
I have all the geometric information about system and also know weight and energy which is transferred.
I need to calculate the support reaction but i can not convert the energy to the force without "impact time". (F * t = m * V )
Also, i m not sure is there any reaction force on the supports because it s a pin connection.
Is it possible to calculate F?
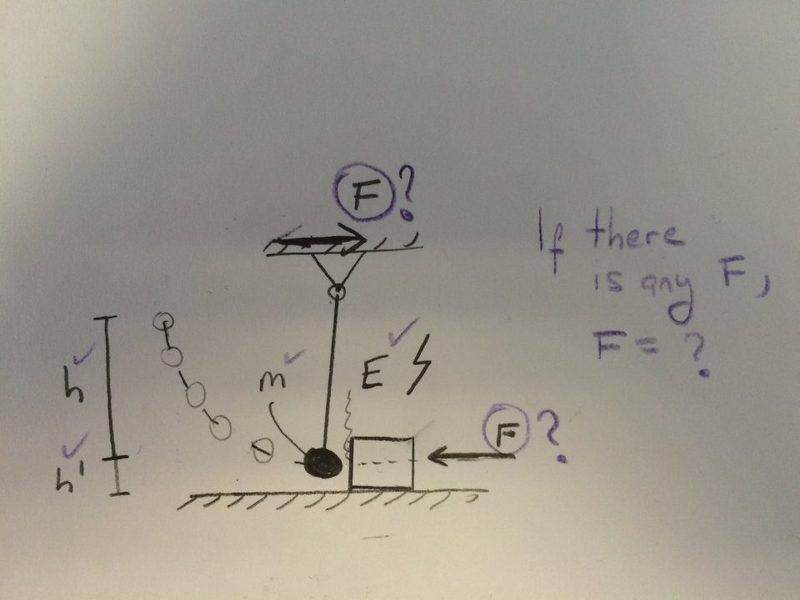
I need to make a "bumper project" as shown in figure.
I have all the geometric information about system and also know weight and energy which is transferred.
I need to calculate the support reaction but i can not convert the energy to the force without "impact time". (F * t = m * V )
Also, i m not sure is there any reaction force on the supports because it s a pin connection.
Is it possible to calculate F?