Calculating the Angle of a Pyramid and Square

[patrickbrans]

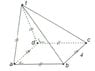
At my math exam i got this picture of a piamide.

Now the question was to calculate the angle made by [tc] and the square (abcd)

how much is that angle?

my thougth was 37°45' and some "can you help me, with a calculation?

the pictur is an attachement and also can be found @ http://www.flagcreator.be/pyramide.png

 

[HallsofIvy]

Is this a "right" pyramid? That is, are you assuming that the vertex of the pyramid is directly over the center of the square? Your picture looks like the pyramid is tilted but if so there is no way to answer this question without knowing the angle of "tilt"- the angle td makes with the square.

If this is a right pyramid, then since td and ta are congruent to the sides of the square base, so are tc and tb. Taking that length to be 1, the diagonals of the base have length $\sqrt{2}$ and the length from c to o, the center of the square, is $\frac{\sqrt{2}}{2}$. The triangle tob, then, is a right triangle, have "near" side to angle tbo, the angle you are asking about, of length $\frac{\sqrt{2}}{2}$ and hypotenuse of length $\sqrt{2}$. The cosine of the angle is the ratio of those: cos(tbo)= 1/2. That is exactly 60 degrees.

If your pyramid is not "right" then more information is needed- imagine, "rotating" triangle adt at different angles about line ad. The angle you are seeking will have different values depending upon that.

 

[neurocomp2003]

there's a right angle at the far side...indicating that t lies on the ad side of a bounding box. pat:Can you show more of your work please?

 

[robphy]

For this question, were you allowed to use coordinate/vector methods?
You have enough information to find coordinates for t, c, and a.

After looking at it again, one could almost do it by inspection... assuming I am looking at it correctly.

 

[neurocomp2003]

you could do it by vector methods...or just simple trig/lenght.

 

[patrickbrans]

the angle between td and tc is 90°
the bottem area is a square with length 4, all lines marked with // are 4

 

[HallsofIvy]

Yes, I missed seeing that "vertical" right angle- my mind just lumped it together with right angles in the base.

But that makes the problem easy: the side is an isosceles right triangle and the angle you seek, angle tcd, is exactly 45 degrees.

 

[patrickbrans]

yes the angle tcd is indeed 45 degrees, but it isn't the same as the angle formed by tc and abcd, becaus i think you calculate that but making the orthagonal (right) projection of tc at abcd, so that would become oc (where o is the middle of ad) and so you get an angle of 37°45' and some secondes

Is that method of thinking correct?

 

[Semo727]

Now, we learn at school the similar things like this. As I know, there can be not just one angle between line and plane. We can just define the smallest angle. Smallest angle in this case would be 33.0152 degrees. Hope my calculations were without mistake. (as they often are) HOw did I get this angle? I used triangle CXT where X is in the middle of AD. I just found out the lenghts of sides of triangle and than I got easily the angle TCX.

 

[neurocomp2003]

pat: i think the arch seconds are a bit higher...still around 37-38.
Show your calcs please. because your concept that tc projects into oc is wrong.