- #1
- 1,126
- 642
- TL;DR Summary
- Is this a 'valid' cross-section ?
Following is a frame carefully chosen from this drone footage. At about 0:29 into the video the drone is directly in front of one of the four faces (if you know Cairo, you will know which one) and moving from left to right. At that point I have paused and 'frame-stepped' till the moment before the drone swings around the right edge of the pyramid. So my question is , does the picture present an accurate cross-sectional view / silhouette of the Great Pyramid ? One obvious concern is that the faint lines one can see (presumably representing one or other particular layer of stonework) on the pyramid face are not quite horizontal.
My plan is to super-impose lines along the pyramid edges and then measure the apex angle as well as the slope angle. And hopefully confirm that the base line along with pyramid edges do indeed accurately constitute an isosceles triangle. Further that if a perpendicular is dropped from the apex, the iso triangle will be divided into two equal Kepler (golden ratio) triangles.
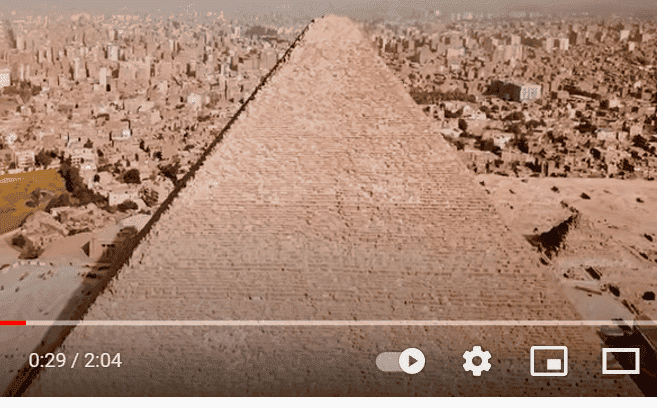
My plan is to super-impose lines along the pyramid edges and then measure the apex angle as well as the slope angle. And hopefully confirm that the base line along with pyramid edges do indeed accurately constitute an isosceles triangle. Further that if a perpendicular is dropped from the apex, the iso triangle will be divided into two equal Kepler (golden ratio) triangles.